194 Глава 8

тивные поля с центром и периферией, но вели себя явно более сложным образом, чем клетки типа 1 наружного коленчатого тела. Они практически не отвечали на белые пятна любых размеров и формы. Но на небольшие цветные пятна, вспыхивающие в центре рецептивного поля, они энергично реагировали в одном диапазоне длин волны и затормаживались в другом диапазоне; некоторые активировались длинными волнами (красным светом) и подавлялись короткими (зеленым и синим светом), другие вели себя противоположным образом. Как и среди клеток коленчатого тела, мы могли, в зависимости от положения максимальных реакций на спектральной шкале, выделить два класса — красно-зеленые и сине-желтые клетки. (Здесь, как и ранее, слова «красный», «зеленый» и «синий» указывают на соответствующие типы колбочек, а слово «желтый» — на параллельные входы от красных и зеленых колбочек.) Таким образом, эти клетки весьма напоминали оппонентно-цветовые клетки коленчатого тела, обладающие только центром (тип 2). Но в отличие от клеток типа 2 эти цветокодирующие пузырьковые клетки чаще всего не отвечали на большие белые или цветные пятна, каков бы ни был спектральный состав света. Они вели себя так, как если бы центральная система рецептивного поля была у них окружена кольцом оппонентности. Если говорить о наиболее распространенном типе клеток, то центр типа r⁺g~, казалось, был окружен у них кольцом типа r~g⁺.

Мы с Маргарет Ливингстон назвали эти клетки двойными оппонентными из-за их красно-зеленой или желто-синей оппонентности в центре и антагонизма периферии по отношению к любой реакции в центре, будь она типа on или off. Поэтому они не отвечают не только на белый свет в любой геометрической конфигурации, но и на большие пятна, независимо от их спектрального состава. Центры рецептивных полей, как и у клеток типа 2, были в несколько раз больше, чем у клеток коленчатого тела типа 1. Как уже упоминалось, Н. Доу ввел термин двойные оппонентные для клеток, обнаруженных им в сетчатке золотой рыбки. Он предполагал, что сходные клетки могли бы участвовать в цвето-пространственных взаимодействиях у человека, и несколько лет спустя совместно с А. Пирлменом он старательно, хотя и безуспешно, искал такие клетки в наружном коленчатом теле макака.

В конце 60-х годов и позже двойные оппонентные клетки изредка находили в коре обезьян, но их не связывали четко с какими-либо анатомическими структурами. Нам до сих пор непонятны некоторые из их особенностей. Например, у только что описанных клеток типа r⁺g~ красное пятно, окруженное зеленым, часто вызывает слабую реакцию вместо энергичной, которой можно было бы ожидать.

Вперемешку с двойными оппонентными клетками обоих классов (красно-зелеными и желто-синими) встречались и обычные широкополосные клетки с центром и периферией. Эти широкополосные клетки отличались от клеток верхних слоев коленчатого тела и от клеток слоя 4СР коры более крупными размерами своих центров.

Мы с Маргарет Ливингстон предположили, что пузырьки представляют собой ветвь зрительного пути, имеющую дело с «цветом» в широком смысле, включая оттенки черного, белого и серого. Эта система, видимо, обособляется от остальной части зрительного пути либо в наружном коленчатом теле, либо в слое 4 стриарной коры. Коленчатое тело, возможно, имеет прямую, хотя и слабую проекцию на пузырьки. Кажется вероятной и проекция на них слоя 4Ср — может быть, для них это даже главный источник входных сигналов. Проецируется ли на них слой 4Са , неясно. Обычно для реакции пузырьковых клеток необходим граничный контраст — нужны либо границы яркости, на которые отвечают широкополосные клетки с центром и периферией, либо цветокон-

ЦВЕТОВОЕ ЗРЕНИЕ 195

трастные границы, на которые реагируют двойные оппонентные клетки. Как уже говорилось, это равнозначно тому, что такие клетки играют роль в создании константности цвета.

Если пузырьковые клетки участвуют в константности цвета, они не могут осуществлять в точности те вычисления, которые рассматривались Лэндом, а именно сравнения между каким-то участком и его окружением для каждого из колбочковых спектральных поддиапазонов. Вместо этого они, по-видимому, осуществляют сравнение по типу Геринга: сопоставляют красно-зеленое в одном участке с красно-зеленым в окружающем фоне и делают то же самое для желто-синего и для интенсивности света. Но оба способа трактовки цвета — г, g и b в одном случае и b-w, r-g, и y-b в другом — по существу, эквивалентны. Цвет требует задания трех переменных: любому цвету соответствует тройка чисел, и мы можем представлять любой цвет точкой в трехмерном пространстве. Точки в таком пространстве можно представлять не единственным способом. Система координат может быть декартовой с осями, расположенными по нашему усмотрению, либо мы можем использовать полярные или цилиндрические координаты. В теории Геринга (в сетчатке и мозгу, наверное, тоже) просто используется иная совокупность осей для описания того же пространства. Эта теория, несомненно, упрощает действительность, так как пузырьковые клетки, принадлежащие к трем классам, вовсе не так сходны между собой,

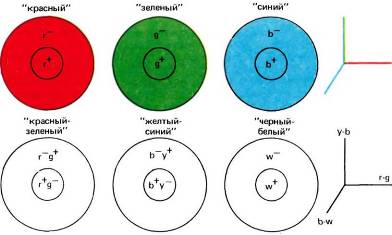
Рис. 130. Вверху: согласно формулировке Лэнда, константность цвета обусловлена наличием трех типов клеток, сравнивающих активацию данного набора колбочек (красных, зеленых или синих) в какой-то области сетчатки со средней активацией такого же набора в окружающей зоне. Результат — три числа, определяющие цвет данной области. Например, желтому, коричневому, темно-серому и оливковому соответствуют определенные тройки чисел. Мы можем, таким образом, отображать цвета в некотором цветовом пространстве с тремя осями, которые соответствуют красному, зеленому и синему.

Внизу: математически эквивалентная система, в которой тоже могут быть заданы три числа. Она, вероятно, ближе к тому способу, которым мозг определяет цвета. В любой точке сетчатки мы можем говорить о степени «красно-зелености», измеряемой неким прибором, регистрирующим относительную силу стимуляции красных и зеленых колбочек (и показывающим нуль для желтого и белого). Эта величина определяется для данной области, а ее среднее значение — для окружения; затем вычисляется отношение этих величин. Тот же процесс повторяется для желто-синей и черно-белой систем. Получаемые три числа достаточны для задания любого цвета.