3.10.Определение основных параметров переходного процесса.

Определение основных параметров системы следует производить с учетом построенного графика h(t) (Приложение 3).

Определим число радиан в фазовом угле, составив пропорцию

и решив ее относительно R

Далее определяем момент времени , когда гармоническая функция равна нулю (Приложение 3), решается равенство

Второй момент времени определяется выражением

В нашем случае согласно построенному графику время регулирования равно t_per=2.95.

3.11.Определение коэффициента качества системы регулирования.

Для определения коэффициента качества системы необходимо вос­пользоваться аналитическим выражением

.

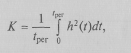
Чтобы упростить вычисления интеграла, площадь, ограниченную функ­цией h(t), заменим площадью четырех треугольников S₁, S₂,S₃ ,S₄(Приложение 3).

3.12.Построение амплитудно-частотных характеристик зве­ньев и системы в целом.

Приступим к определению амплитудно-частотных характеристик зве­ньев и системы в целом. Для определения частотной характеристики объекта регулирования произведем замену в передаточной функции объекта.

Имеем , сделав замену p=iw получим частотную характеристику объекта регулирования (Приложение 4).

Определим частотную функцию датчика

Для выделения действительного и мнимого значений умножаем чис­литель и знаменатель на комплексно-сопряженное значение знаменателя:

В результате получим действительную и мнимую части. Далее опреде­лим модуль, полагая, что

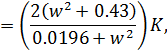
Где K= . Если в это выражение подставить текущие значения w, то получим К ≈ 1.

Далее строим график, зная, что

(Приложение 4).

Определим спектральную характеристику исполнительного меха­низма

Произведем замену в передаточной функции исполнительного механизма:

Здесь для построения спектральной характеристики исполнитель­ного механизма даются текущие значения w и определяется А_{и. м}(w) (Приложение 4).

Определим спектральную характеристику регулятора.

Передаточная функция имеет вид

Примем р = iw и получим

Для выделения действительного и мнимого значений умножим чис­литель и знаменатель на комплексно-сопряженное выражение знаме­нателя:

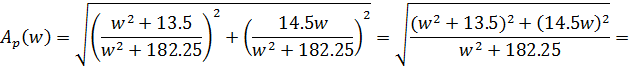
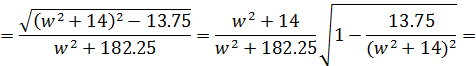
Далее строим график (Приложение 4) с учетом выражения

Определим частотную характеристику цепи обратной связи ДРИМ. Имеем передаточную функцию

Для определения спектральной характеристики цепи обратной связи — ДРИМ — воспользуемся выражением

Здесь необходимо для каждого текущего значения w определять орди­наты в частотных характеристиках датчика, регулятора и исполнитель­ного механизма и перемножать их. В результате этого действия получим следующие значения:

w	0.2	0.5	1	2
A	1.7	0.22	0.06	0.02

По этим значениям строится частотный спектр цепи обратной связи (Приложение 5).

Частотную характеристику всей системы можно записать выражением

Здесь также очень сложные аналитические преобразования. Для построения частотной характеристики всей системы следует учи­тывать функциональную связь

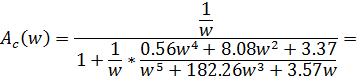
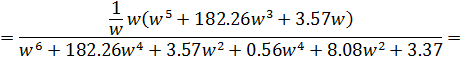
Подставим текущие значения частоты в это выражение и определим значения ординат спектральной характеристики системы:

w	0	1	2	3
A	1	0.9	0.5	0.3

По этим значениям строится частотная характеристика всей системы (Приложение 5).