
- •5. Элементы теории графов
- •5.1. Основные понятия
- •5.2. Определение и способы задания графов определение
- •1. Списки ребер
- •2. Матрицы смежности
- •3. Матрицы инциденций
- •4. Списки смежности
- •5.3. Изоморфизм графов
- •Определение
- •5.4. Планарность графов
- •Определение
- •Определение
- •Определение
- •Определение
- •5.5. Пути и связность в графах
- •Определение
- •Определение
- •Упражнения
- •5.6. Транзитивное замыкание графов определение
- •5.7.Деревья
- •Определение
- •Определение
- •Теорема 5.4
- •Определение
- •5.8. Цикломатика графов
- •5.8.1. Циклы эйлера и гамильтона
- •Определение
- •Доказательство
- •Индуктивное предположение
- •Определение
- •5.8.2. Фундаментальное множество
- •Доказательство
- •Определение
- •Теорема 5.8
- •5.9. Внутренне и внешне устойчивые
- •Определение
- •Определение
- •Определение
- •Определение
- •Теорема 5.10
- •Теорема 5.11
- •Доказательство
- •5.10. Хроматическое число графа
- •Определение
- •Определение
- •Теорема 5.12
- •Теорема 5.13
- •Доказательство
Определение
Граф называется плоским, если он имеет геометрическую реализацию на плоскости.
Для плоских графов применяется еще одно наименование планарные графы.
В се
приводившиеся ранее примеры графов
являются плоскими графами. Однако не
всякий граф является планарным. Например,
графы, изображенные на рис. 5.6,
не имеют геометрических реализаций на
плоскости. a
се
приводившиеся ранее примеры графов
являются плоскими графами. Однако не
всякий граф является планарным. Например,
графы, изображенные на рис. 5.6,
не имеют геометрических реализаций на
плоскости. a
a b c
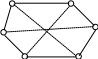
K3,3 b c A 5
1 2 3
d e
Рис. 5.6.
ТЕОРЕМА 5.2
Графы K3,3 и A5 не являются плоскими.
Доказательство
Покажем, что K3,3 это непланарный граф.
Предположим противное. Возьмем произвольную геометрическую реализацию этого графа на плоскости.
Рассмотрим последовательное прохождение вершин K3,3 в следующем порядке: a 2 b 3 c 1 a. В рассматриваемом геометрическом представлении K3,3 на плоскости этому прохождению соответствует перемещение по некоторой замкнутой линии, не имеющей самопересечений.
Эта линия содержит все вершины графа и 6 ребер, а также делит плоскость на две части: внутреннюю, ограниченную замкнутой линией, и внешнюю. В общем виде возникающая ситуация представлена на рис. 5.7:
 a
2
a
2
1 b
c 3
Рис. 5.7
Во внутренней и внешней областях должны быть изображены 3 ребра (которые обозначены на рисунке пунктирными линиями). Поэтому хотя бы в одной из этих областей необходимо провести не менее двух ребер. Нетрудно проверить, что во внутренней области невозможно провести более одного ребра так, чтобы соответствующие дуги не пересекались. Рассмотрим случай, когда во внутренней области изображается ребро (a, 3). Тогда ребра (b,1) и (c,1) должны изображаться дугами во внешней области. Но при любом изображении ребра (b,1) концы последнего ребра (c,1) невозможно соединить без пересечения уже проведенных линий. Это так поскольку всегда найдется такая замкнутая область на плоскости, образованная линиями, изображающими рёбра, что одна из вершин c и 1 содержится внутри, а другая снаружи этой области.
Поэтому предположение о существовании геометрической реализации графа K3,3 является неверным.
Непланарность графа A5 доказывается аналогично приведенному доказательству непланарности графа K3,3.
Доказательство окончено.
В определенном смысле графы K3,3 и A5 являются каноническими непланарными графами. Оказывается, что все другие непланарные графы содержат в себе фрагменты, подобные либо графу K3,3, либо графу A5.
Для того чтобы сформулировать критерий планарности графов, определим дополнительные понятия.
Определение
Граф
G1
= (V1,U1)
называется подграфом графа
G2
= (V2,
U2),
если V1
![]() V2
и U1
U2.
V2
и U1
U2.
Например, граф G1, приведенный на рис. 5.8., является подграфом графа G2.

a G 2 a G 1
b b
c c
d
Рис. 5.8.
Удаление из графа G некоторой вершины v, степень которой равна 2, это замена удаляемой вершины и двух выходящих из нее ребер на одно ребро, соединяющее отличные от v концы удаленных ребер.
Процесс последовательного удаления из графа G одной или нескольких вершин степени 2 называется стягиванием этого графа. Обратная операция для удаления вершин степени 2 называется разбиением ребер.
Заметим, что операции удаления из графа вершин степени 2 и разбиения ребер сохраняют свойства графов быть планарными или непланарными.
ОПРЕДЕЛЕНИЕ
Разбиением ребра u = (a, b) графа G называется замена в этом графе ребра u на два ребра u1 = (a, c) и u2 = (c, b), где c это новая вершина, не являющаяся вершиной G.
