
- •5. Элементы теории графов
- •5.1. Основные понятия
- •5.2. Определение и способы задания графов определение
- •1. Списки ребер
- •2. Матрицы смежности
- •3. Матрицы инциденций
- •4. Списки смежности
- •5.3. Изоморфизм графов
- •Определение
- •5.4. Планарность графов
- •Определение
- •Определение
- •Определение
- •Определение
- •5.5. Пути и связность в графах
- •Определение
- •Определение
- •Упражнения
- •5.6. Транзитивное замыкание графов определение
- •5.7.Деревья
- •Определение
- •Определение
- •Теорема 5.4
- •Определение
- •5.8. Цикломатика графов
- •5.8.1. Циклы эйлера и гамильтона
- •Определение
- •Доказательство
- •Индуктивное предположение
- •Определение
- •5.8.2. Фундаментальное множество
- •Доказательство
- •Определение
- •Теорема 5.8
- •5.9. Внутренне и внешне устойчивые
- •Определение
- •Определение
- •Определение
- •Определение
- •Теорема 5.10
- •Теорема 5.11
- •Доказательство
- •5.10. Хроматическое число графа
- •Определение
- •Определение
- •Теорема 5.12
- •Теорема 5.13
- •Доказательство
Определение
Цикл в некотором графе называется циклом Гамильтона, если он содержит все вершины этого графа по одному разу.
То есть любые две вершины цикла Гамильтона, одна из которых является внутренней вершиной цикла, разные.
Исторически понятие такого цикла относится к головоломке, предложенной в 1859 году Уильямом Гамильтоном. Она называлась задачей о кругосветном путешествии.
В этой задаче предлагалось составить план проезда по странам, имеющим общие границы, так, чтобы побывать в каждой стране ровно по одному разу и вернуться в исходную страну. Данная задача является задачей нахождения циклов Гамильтона в графах, соответствующих географическим картам. Каждой такой карте можно поставить в соответствие граф, вершины которого представляют отдельные государства, а ребра указывают на наличие общей границы между парами государств.
В общем случае граф может не иметь циклов Гамильтона. Например, граф G1, изображенный на рис. 5.20 не имеет таких циклов, так как вершина v при всяком прохождении по всем вершинам этого графа должна проходиться не менее двух раз. Граф G2 имеет цикл Гамильтона. Такой цикл представлен ребрами, изображенными более толстыми линиями.

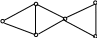
v
G1 G2
Рис. 5.20
Вершина v графа G называется разделяющей, если удаление из G вершины v вместе с соответствующими ей ребрами разбивает граф на несколько компонент связности.
Упражнение. Показать, что если связный граф G имеет разделяющую вершину, то G не имеет цикла Гамильтона.
Практически важная задача, приводящая к поиску циклов, близких по свойствам к циклам Гамильтона, носит название задачи коммивояжёра.
В этой задаче требуется определить такой маршрут движения торговца между населенными пунктами (магазинами), чтобы торговец побывал в каждом пункте, вернулся в начало пути, и суммарная длина пройденного пути оказалась минимальной.
Разновидностью приведенной задачи является задача нахождения цикла Гамильтона.
Для нахождения циклов Гамильтона в произвольных графах можно воспользоваться процедурой перебора вариантов. Для произвольно заданного графа G, имеющего n вершин, достаточно организовать последовательную проверку всех перестановок вершин этого графа. Каждая такая перестановка дополняется вершиной, равной её первому элементу, после чего проверяется свойство полученной последовательности вершин быть циклом Гамильтона в G.
Практическая применимость такого переборного метода сомнительна, поскольку число перестановок вершин, равное n!, уже для небольших по размерам графов является слишком большим.
Замечание. Для циклов Гамильтона, в отличие от циклов Эйлера, неизвестны непереборные алгоритмы нахождения таких циклов в произвольных графах. Более того, существующая теория решения комбинаторных задач относит задачу отыскания таких циклов в графах к классу наиболее длительных по времени решения задач.
Поэтому рассмотрение задачи нахождения циклов Гамильтона в графах естественно ограничить рассмотрением отдельных классов графов, для которых могут быть получены простые по сложности проверки условия существования таких циклов.
В качестве примера рассмотрим одно простое достаточное условие существования циклов Гамильтона для графов без петель, основанное на специальном свойстве степеней вершин таких графов.
Пусть
G
=
(V,
U)
некоторый граф без петель и V
= {a1,
... , an}.
Будем считать, что n
![]() 3.
3.
ТЕОРЕМА 5.6
Если
![]() ai,
aj
V(d(ai)
+
d(aj)
n),
то граф G
имеет цикл Гамильтона.
ai,
aj
V(d(ai)
+
d(aj)
n),
то граф G
имеет цикл Гамильтона.
Доказательство
Возьмем произвольную циклическую последовательность (1), состоящую из всех вершин графа G (рис. 5.21).
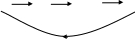 a
1
a
2
. . . an
(1)
a
1
a
2
. . . an
(1)
Рис. 5.21
Будем говорить, что в последовательности (1) имеется разрыв между вершинами ai и ai+1, если (ai, ai+1) U, т.е. если эти вершины не соединяет ребро.
Понятно, что в последовательности (1) может иметься лишь конечное число разрывов.
Покажем, что эту последовательность можно преобразовать в такую циклическую последовательность, которая не содержит разрывов и, следовательно, является циклом Гамильтона в G.
Последнее утверждение является верным, если в (1) нет разрывов.
Предположим, что в (1) имеются разрывы.
Без ограничения общности можно считать, что в (1) имеется разрыв между вершинами a1 и a2. В противном случае следует по-другому определить начало этой циклической последовательности.
Покажем, что среди остальных вершин последовательности (1) найдутся такие две последовательно идущие вершины ai и ai+1, что (a1, ai) U и (a2, ai+1) U.
Так как вершины a1 и a2 не являются соседними, то вершины, соседние с a1 или a2, содержатся среди n 2 вершин последовательности:
a3, ... , an |
(2) |
Предположим, что в (2) нет двух последовательно идущих
вершин, первая из которых является соседней с a1, а вторая соседней с a2.
В последовательности (2) содержится не менее чем d(a1) 1 вершин, не соседних с a2. Это следует из того, что после всякой вершины в (2), соседней с вершиной a1, следует вершина, которая не является соседней с a2.
Среди элементов последовательности (2), отличных от an, содержится не менее чем d(a1) 1 вершин, соседних с a1 и после каждой такой вершины расположена вершина, не соседняя с вершиной a2.
Поскольку вершины a1 и a2 также не являются соседними с вершиной a2, то общее число вершин графа G, не соседних с a2, не менее d(a1) + 1.
Всякая вершина в G либо является соседней с a2 либо не является соседней с a2. Поэтому общее число вершин графа G должно удовлетворять неравенству
n d(a1) + d(a2) + 1.
Последнее неравенство противоречит условиям теоремы, из которых следует, что d(a1) + d(a2) n.
Следовательно, в последовательности (1) имеется пара соседних вершин ai и ai+1, для которых (a1, ai) U и (a2,a i+1) U.
Воспользуемся доказанным свойством вершин a1 и a2 и переставим вершины в (1) так, как это указано на рис. 5.22.:
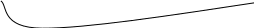

a 1 a2 . . ai ai +1 . . . an (3)
Рис. 5.22
В результате данного преобразования образуется новая циклическая последовательность, содержащая все вершины графа G, в которой меньше разрывов, чем в исходной последовательности (1).
Будем повторять описанное преобразование до тех пор, пока в получаемых циклических последовательностях имеются разрывы.
Через конечное число шагов из последовательности (1) будет получена циклическая последовательность вершин, не содержащая разрывов. Она образует цикл Гамильтона в графе G.
Доказательство окончено.
СЛЕДСТВИЕ (Теорема Дирака)
Пусть
G
= (V,
U)
неориентированный связный граф без
петель и |V|
=
r.
Тогда если для всякой вершины v
V
справедливо
неравенство d(v)
![]() , то G
имеет
цикл Гамильтона.
, то G
имеет
цикл Гамильтона.
Заметим, что приведенное доказательство теоремы 5.6 является конструктивным, поскольку оно содержит явный алгоритм построения цикла Гамильтона во всяком графе, для которого выполняются условия этой теоремы.
