5 Схема симплекс – метода

Рассмотренный ранее способ перехода от одного ДБР к другому, а также последние теоремы позволяют построить так называемый симплекс – метод решения ЗЛП в канонической форме, который имеет следующую схему:

(не давать – методич. указаниях)

Шаг 0. Построение начального ДБР

Найти некоторое ДБР исходной ЗЛП (такое ДБР называется начальным). Пусть данному ДБР соответствует

• базис В,

• базисная матрица В,

• небазисная матрица N,

• вектор базисных переменных ,

• небазисных переменных ,

• вектор оценок ограничений . (в опт.реш. это ценности ресурсов)

Шаг 1. Вычисление компонент вектора относительных оценок небазисных переменных.

.

Шаг 2. Проверка выполнения условия оптимальности.

Если выполняется , то прекратить вычисления – текущее ДБР является решением исходной задачи.

Шаг 3. Выбор небазисной переменной , вводимой во множество базисных переменных.

Выбрать p, для которого

(Обычно р соответствует минимальная отрицательная компонента = максимальная по модулю отрицательная)).

Шаг 4. Выбор базисной переменной, исключаемой (выводимой) из множества базисных переменных.

Вычислить элементы ведущего столбца: .

Условие допустимости

Если , то прекратить вычисления – целевая функция не ограничена сверху.

Иначе выбрать q, для которого выполняется , т.е. переменная будет исключена из множества базисных переменных.

Шаг 5. Операция замещения.

Построить базис нового ДБР путем замены столбца текущего базиса В на столбец . Построить новую базисную матрицу В и небазисную . Найти новое ДБР с . Перейти на шаг1.

Последовательность шагов 1-5 называется итерацией симплекс – метода.

Если имеем ЗЛП на минимум, то достаточным условием оптимальности является условие .

На практике число итераций , а общее время счета = ( - коэффициент пропорциональности, зависящий от типа задачи).

Хотя можно подобрать пример, в котором перебираются все вершины. кубик:

Самостоятельно №

Показать, что из того, что мы выбираем , не следует, что получим максимальный прирост ЦФ, более того, можно подобрать пример, когда будет наоборот.

Сходимость с-м

[Ермольев, с.22]

Если после каждой итерации значение ЦФ увеличивается, то симплекс-методом перебираются различные вершины. Т.к. вершин конечное число, то за конечное число итераций будет получено решение задачи. Если же после некоторой итерации значение ЦФ не увеличивается , то в процессе перебора некоторые вершины могут повторяться и не исключено, что может быть получена последовательность ДБР периодически повторяющихся и не являющихся оптимальным решением ЗЛП. Это явление называется зацикливанием.

Если задачи имеют небольшие размерности, случаи зацикливания редки. Однако, вероятность этого растет по мере роста размерности задачи. [Муртаф, с.30]

С геометрической точки зрения зацикливание объясняется вырожденностью текущего решения.

С практической точки зрения вырожденность объясняется наличием избыточных ограничений:

С вычислительной точки зрения, причина зацикливания – не единственность выбора выводимой переменной.

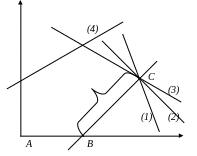
Точке С соответствует базисов. Например

Расстояние от т.В до прямых (1), (2), (3) одно и то же:

(1)

(2)

Три отношения принимают минимальное значение, но выводим из базиса только одну переменную, две другие оставаясь базисными принимают нулевое значение.

[Таха, с. 114-116]

В ходе выполнения симплекс-метода проверка условия допустимости приводит к неоднозначному выбору исключаемой переменной (т. В)). В этом случае перейдём к вырожденному решению (одна или несколько базисных переменных примут нулевое значение) (т. С). Если на следующей итерации при выбранном p будет существать i такое, что и , то в результате выполнения такой итерации мы перейдем к новому базису не изменившегося ДБР (останемся в т. С).

БП

X5↓

БП

X6↓

БП

X2↓

z

z

z

x1 ←

0

x5

0

x5

0

x2

x2

x2

x3

x3

x3

x4

0

x4 ←

0

x6 ←

0

Чтобы исключить зацикливание, был разработан ряд приёмов.

1. Вырожденному ДБР геометрически соответствует вершина в n – мерном протстрантве, которая получается пересечением гиперплоскостей, число которых больше n. Поэтому, заменив вектор b на вектор b() можем добиться того, чтобы каждая вершина была пересечением n гиперплоскостей

Т.е. задача

заменяется задачей

Для исключения вырожденности в вектор b вносятся небольшие возмущения:

,

 - достаточно малое.

Тогда, если b() – вектор правых частей и B= - текущий базис, то

. (3)

Самостоятельно №

Объяснить почему (3) справедливо.

Прямые слегка смещаются и  (2) не выполняются, то есть в (1) минимум единственный.

Отсюда видим, что теперь можно однозначно определить переменную, выводимую из базиса (бывшие нулевые базисные переменные принимают разные ненулевые значения).

После получения оптимального решения нужно будет опять перейти к исходному вектору .

2. Второй, более эффективный, прием устранения зацикливания был разработан Блендом. (Ашманов, Тимохов, стр.146)

Сначала определим два множества, пусть

- множество индексов (номеров) базисных переменных;

- множество индексов (номеров) небазисных переменных.

Теорема Бленда(правило устранения зацикливания)

Если переменная, вводимая в базис определяется так:

,

а переменная, выводимая из базиса так:

,

где , то зацикливание симплекс-метода невозможно.

Без доказательства.

ИТАК:

Если исходная ЗЛП является невырожденной, то очевидно, что симплекс – метод за конечное число шагов находит решение задачи (если применить правило Блэнда, то и для вырожденной ЗЛП получим решение за конечное число шагов).

21