Практические результаты использования модели Леоньева
Оценка инфляционного влияния в регулировании заработной платы
Расчет затрат на вооружение и их воздействие на разные отрасли экономики
Прогнозирование темпа роста отраслей экономики и необходимые для этого капитальные вложения
Шахматные балансы по методу Леонтьева стали составляться для хозяйства отдельных американских городов. Постепенно составление таких балансов стало стандартной операцией.
ООН, Всемирный банк и большая часть правительств различных стран мира, включая СССР, взяли на вооружение метод Леонтьева в качестве важнейшего метода экономического планирования и бюджетной политики
Анализ по методу «затраты-выпуск» признан классическим инструментом экономического анализа, а его автор считается ученым, внесшим крупнейший вклад в экономическую науку XX века.
В 1973 году Леонтьев был удостоен Нобелевской премии по экономике «за развитие метода «затраты-выпуск» и его применение к решению важных экономических проблем»
Содержательная постановка задачи линейного программирования (планирования)
Фабрика производит два вида красок К1 и К2.
Для производства красок используются два ингредиента: А и В.
Известны их суточные запасы этих ингредиентов и их расход при производстве 1 т красок (таблица).
Изучение рынка сбыта показало, что:
суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т;
спрос на краску 2-го вида никогда не превышает 2 т в сутки;
Оптовые цены красок: для К1–3 тыс. руб./т ; для и К2– 2 тыс. руб./т
Необходимо определить составить план производства красок, обеспечивающий максимальный доход от их реализации.
Параметры задачи о производстве красок
Ингредиенты |
Расход ингредиентов, т ингр./т краски |
Запас, т ингр./сутки |
|
К1 |
К2 |
||
А |
1 |
2 |
6 |
В |
2 |
1 |
8 |
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
ГРАФИЧЕСКОЕ РЕШЕНИЕ
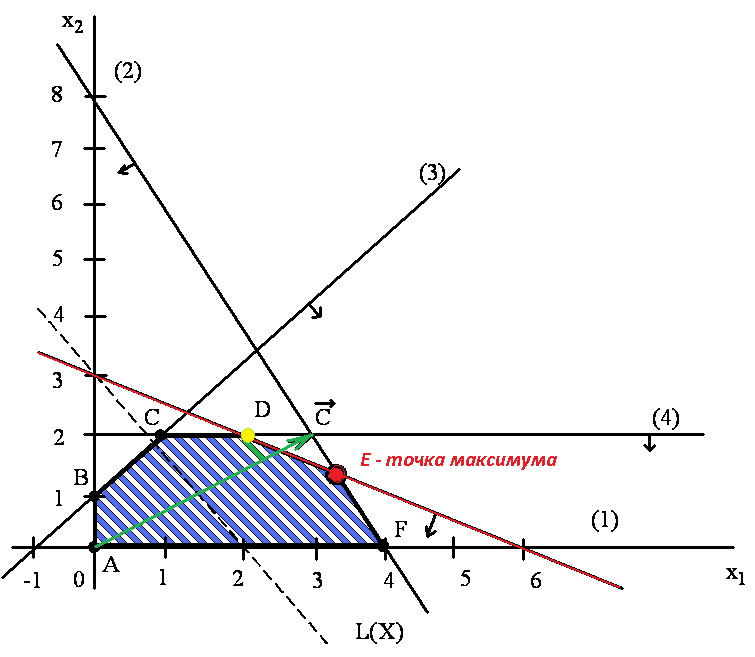
МАТЕМАТИЧЕСКИЙ ОТВЕТ
[т/сутки]
[тыс. руб./сутки]
СОДЕРЖАТЕЛЬНЫЙ ОТВЕТ
Рекомендуемый план производства К1– 3,33 т/сут.; К2– 1,33 т/сут.
Ожидаемый доход от продажи красок 12,67 тыс. руб./сут.
АНАЛИЗ РЕШЕНИЯ
1. Анализ сокращения или увеличения ресурсов:
на сколько можно увеличить (ограничения типа
)
запас дефицитного
ресурса для улучшения оптимального
значения ЦФ?на сколько можно уменьшить (ограничения типа ) запас недефицитного ресурса при сохранении оптимального значения ЦФ?
2. Увеличение (ограничения типа ) запаса какого из ресурсов наиболее выгодно?
3. Анализ изменения коэффициентов ЦФ: каков диапазон изменения цен на краски (коэффициентов ЦФ), при котором не меняется оптимальное решение?
Примеры выводов
Предельный уровень, до которого может упасть спрос на краску К2 при котором не изменится оптимальность полученного ранее решения, равен 1,33 т/сут.
Максимальное превышение спроса на краску К1 над спросом на краску К2, при котором оптимальное решение в точке Е не изменится, составляет 2 т/сут
Дополнительные вложения в первую очередь необходимо направлять на увеличение ресурса В, а лишь потом на ресурс А
Если цены на краску К1 будут колебаться в пределах от 1 до 4 тыс. руб./т, то оптимальное решение задачи не изменится
Если цена на краску К1 станет меньше 1 тыс.руб./т, то наиболее выгодным будет производство красок в точке D