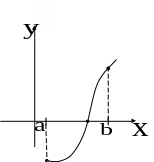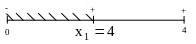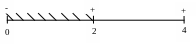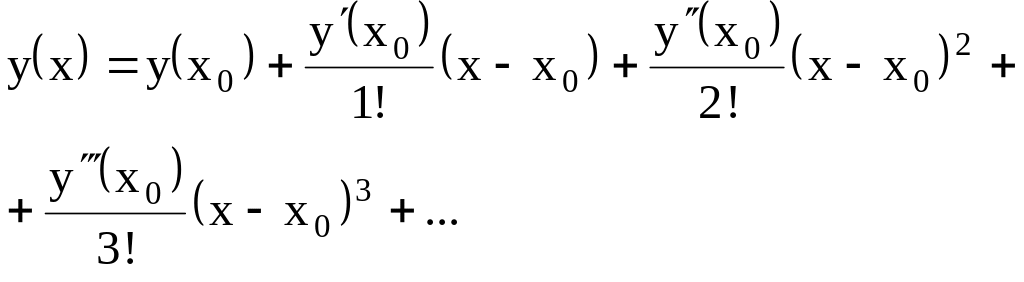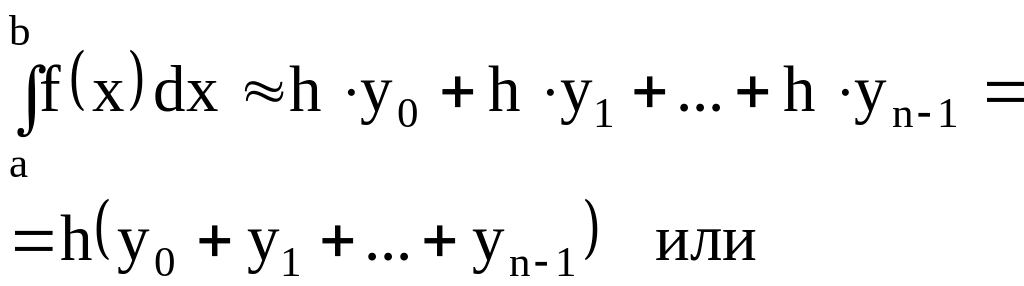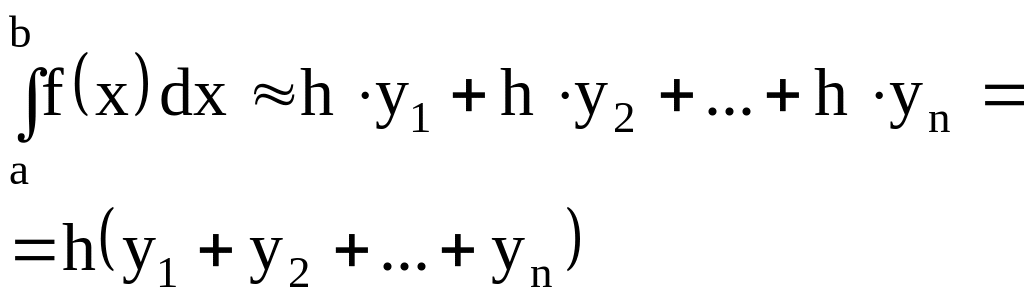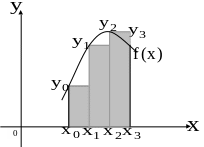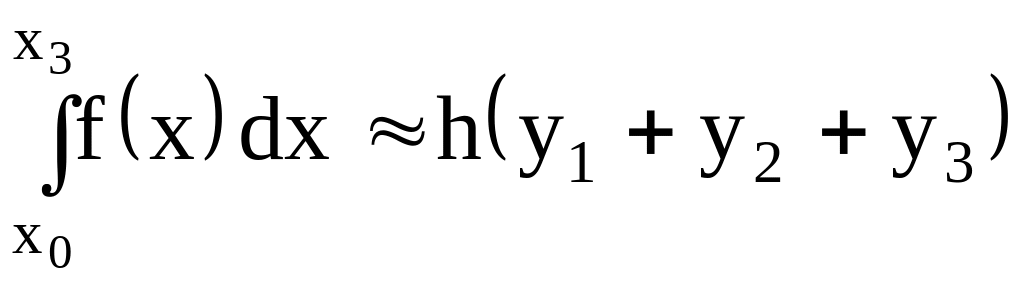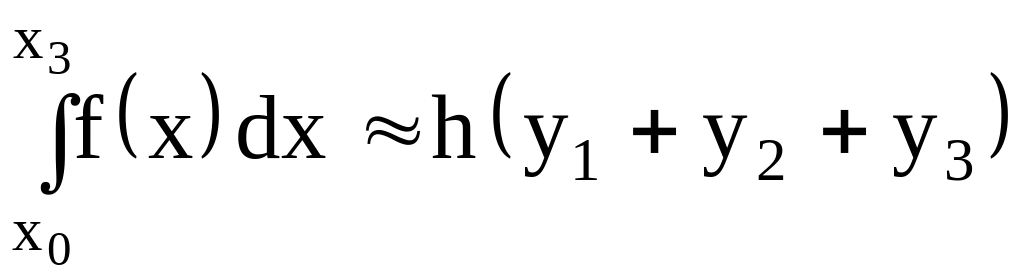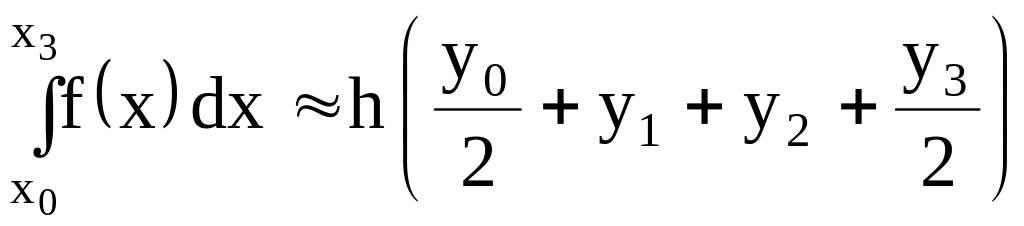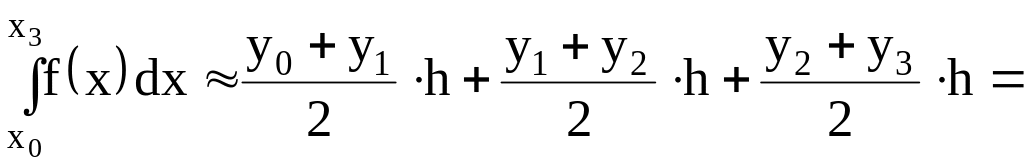Глава 22. Интерполирование

Интерполирование

Задача

Пусть дана таблица значений

			…
			…

Требуется составить полином степени , график которого должен проходить через заданные точки .

Обозначим через

Вспомогательный многочлен n-й степени, в котором - заданные табличные значения аргумента. Тогда

Задача.

Составить полином Лагранжа, удовлетворяющий таблице значений

x	1	2	3	4
y	2	3	4	5

Решение.

Вспомогательный многочлен имеет вид . Вычислим последовательно при данных значениях :

, , , .

Тогда

Таким образом, в данном случае интерполяционный полином есть линейная функция .

Это и есть интерполированный полином Лагранжа.

Задача.

График функции проходит через точки

	1	2	3
	5	7	11

Тогда ее интерполяционный многочлен второго порядка равен…

Варианты ответов: 1) 2)

3) 4)

Решение.

Так как график функции должен проходить через заданные точки, подставим координаты точек в каждый из многочленов.

1)

Все равенства верные.

Проверив все остальные многочлены, убеждаемся, что их графики проходят не через все данные точки.

Ответ: №1.

Вычисление приближенного значения функции

(*)

Задача.

Значение функции в точке можно вычислить по формуле…

Варианты ответов:

1)

2)

3)

4)

Решение.

, тогда

Найдем производную ; .

Тогда .

Подставим в формулу (*)

Ответ. №1

Приближенное решение уравнений

Если для уравнения известно, что

1) - непрерывная функция на отрезке

2) на отрезке уравнение имеет единственный корень.

Тогда функция на концах отрезка принимает значения разных знаков, т.е.

и или наоборот и .

С геометрической точки зрения.

Задача.

Действительный корень уравнения принадлежит интервалу…

Варианты ответов: 1) 2)

3) 4)

Решение.

.

Рассмотрим первый интервал .

.

.

Рассмотрим второй интервал .

.

.

Рассмотрим третий интервал

.

.

Рассмотрим четвертый интервал

.

.

Только на четвертом интервале на концах функция принимает значения разных знаков, следовательно, корень уравнения принадлежит четвертому интервалу.

Ответ. №4.

Задача.

Действительный корень уравнения принадлежит интервалу…

Варианты ответов: 1) 2)

3) 4)

Решение.

Рассмотрим первый интервал

На концах отрезках функция принимает значения разных знаков. Следовательно, корень принадлежит данному интервалу.

Ответ. №1.

Метод половинного деления

Основан на утверждении:

при делении отрезка пополам выбирается тот отрезок, на концах которого функция имеет разные знаки.

Середина отрезка вычисляется по формуле

Задача.

Три итерации метода половинного деления при решении уравнения на отрезке требуют последовательного вычисления значений функции в точках…

Варианты ответов: 1)

2) 3)

4)

Решение.

Найдем значения функции на концах заданного отрезка .

Середина отрезка :

Значение функции в середине

Выбираем отрезок с разными знаками. Это отрезок .

Найдем середину этого отрезка .

Значение функции в середине .

Выбираем отрезок с разными знаками. Это отрезок .

Найдем середину отрезка :

Ответ. №1

Решение дифференциального уравнения с помощью разложения функции в степенной ряд

Степенной ряд для функции имеет вид

Если , то

(**)

Задача.

Дано дифференциальное уравнение при . Тогда первые три члена разложения его решения в степенной ряд имеют вид…

Варианты ответов: 1) 2)

3) 4)

Решение.

Из формулы (**) видно, что нужно найти .

По условию задачи , т.е. ; .

Т.к. , то .

Найдем производную от обеих частей исходного уравнения

, получим .

Подставим уже полученные , .

Тогда .

Полученные значения , и подставим в степенной ряд (**)

Ответ. №1.

Приближенное вычисление определенных интегралов

С геометрической точки зрения, если на , тогда - площадь криволинейной трапеции, ограниченной прямыми , , осью и графиком функции .

Метод прямоугольников

Имеют место следующие формулы

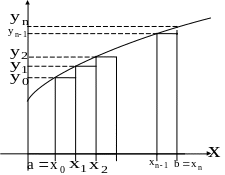
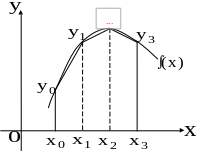
Задача.

Формула приближенного вычисления определенного интеграла, соответствующая рисунку, имеет вид…

Варианты ответов: 1)

2)

3)

4)

Решение.

Определенный интеграл приближенно равен сумме площадей заштрихованных прямоугольников

Ответ. №3.

Метод трапеций

Задача.

Формула приближенного вычисления определенного интеграла, соответствующая рисунку, имеет вид…

Варианты ответов: 1)

2)

3)

4)

Решение.

Определенный интеграл приближенно равен сумме площадей заштрихованных трапеций

Ответ. №4.

Метод Эйлера решения дифференциального уравнения

Решение дифференциального уравнения , удовлетворяющего начальному условию можно приближенно определить в точках

;

и т.д.,

где - шаг изменения аргумента

(***)

Задача.

Найти, используя метод Эйлера, значения функции , определяемой дифференциальным уравнением при начальных условиях , принимая .

Ограничиться отысканием первых трех значений .

Варианты ответов: 1) ; ;

2) ; ;

3) ; ;

Решение.

1) Из начального условия ; .

Найдем .

2)

Для вычисления воспользуемся формулой (***)

3)

.

Ответ. №2.