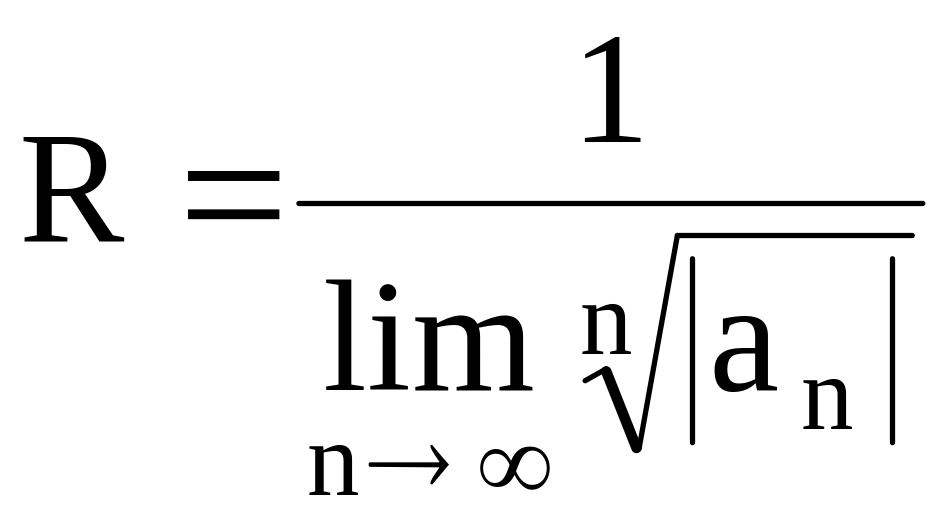Глава 17. Дифференциальные уравнения в частных производных

Если в дифференциальных уравнениях независимых производных две или больше, то дифференциальное уравнение называется дифференциальным уравнением в частных производных.

§1 Дифференциальное уравнение первого порядка

, (1)

где , и - функции , и .

1. Решение дифференциального уравнения первого порядка в частных производных.

Предварительно решить систему обыкновенных дифференциальных уравнений

.

Пусть решение этой системы определяется равенствами

,

.

Тогда общий интеграл дифференциального уравнения (1) имеет вид

,

где - произвольная непрерывно-дифференцируемая функция.

§2 Дифференциальное уравнение второго порядка

, (2)

где - функции и .

1. Типы дифференциальных уравнений второго порядка в частных производных

Если , то уравнение (2) принадлежит гиперболическому типу.

каноническое уравнение гиперболического типа.

Если , то уравнение (2) принадлежит параболическому типу.

каноническое уравнение параболического типа.

Если , то уравнение (2) принадлежит эллиптическому типу.

называется каноническое уравнение эллиптического типа.

Задача.

Общее решение дифференциального уравнения в частных производных первого порядка имеет вид следующей непрерывно дифференцируемой функции…

Варианты ответов: 1) 2) 3) 4)

Решение.

Запишем систему уравнений: . Решая , получаем , решая , получаем . Общий интеграл имеет вид: , откуда

Ответ. №2.

§1 Общие сведения

1. Ряд. Общий член ряда

Выражение вида , где - члены некоторой бесконечной последовательности, называется рядом, называется общим членом ряда.

Сумма называется частичной суммой ряда

2. Сходимость ряда. Сумма ряда

Ряд называется сходящимся, если , при этом число называется суммой ряда.

Ряд называется расходящимся, если не существует или бесконечен.

Задача.

Частичная сумма первых пяти членов числового ряда 11; 13; 15; … , равна … .

Варианты ответов: 1) 75 2) 19 3) 47,5 4) 80

Решение.

.

Ответ. №1.

Задача.

Общий член последовательности имеет вид…

Варианты ответов: 1) 2) 3) 4)

Решение.

Из предложенных ответов не подходят №2 (так как при получаем отрицательное число ), и №3 (так как нет чередования знаков).

В формулы №1 и №4 подставляем натуральные значения n.

Если , то , не подходит.

Если , то , , , , … подходит.

Ответ. №4.

Задача.

Второй член числового ряда равен…

Решение.

.

Ответ. 16.

§2 Числовые ряды

3. Гармонический ряд

4. Обобщенный

гармонический ряд

5. Ряд геометрической

прогрессии

Ряд

называется гармоническим рядом. Он расходится.

Ряд

называется обобщенным гармоническим рядом.

Ряд

Ряд , называется рядом геометрической прогрессии.

Этот ряд при

1) сходится, его сумма равна

2) расходится

Задача.

Укажите сходящиеся числовые ряды.

Варианты ответов: 1) 2)

3) 4)

Решение.

;

;

.

Все ряды являются обобщенными гармоническими рядами, т.е. рядами вида . При - ряд расходится, поэтому ответ №3.

Ответ. №3.

Задача.

Сумма числового ряда равна…

Варианты ответов: 1) 2) 3) 4)

Решение.

Ряд - ряд геометрической прогрессии.

,

, , .

Ответ. №2.

6. Необходимое условие сходимости ряда (не является достаточным)

Если ряд сходится, то его общий член стремится к нулю, т.е. .

Задача.

Из данных рядов выбрать те, для которых не выполняется необходимое условие сходимости ряда 1) 2) 3) 4)

Решение.

1) , выполняется.

2) , не выполняется.

3) , выполняется.

4) , выполняется.

Ответ. №2.

§3 Знакоположительные ряды. ,

7. Достаточные признаки сходимости ряда

7.1. Признак Даламбера

7.2. Радикальный признак Коши

7.3. Интегральный признак Коши

7.4. Признаки сравнения

Если в ряде с положительными членами выполняется условие

, то

1) при , данный ряд сходится

2) при , данный ряд расходится

Если в ряде с положительными членами , то

1) при , данный ряд сходится

2) при , данный ряд расходится

Если члены знакоположительного ряда могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке функции так, что , , … , , … , то:

1) и ряд сходятся или расходятся одновременно

I. Пусть даны два знакоположительных ряда и

Если для всех n выполняется неравенство

, то

а) из сходимости ряда с большими членами следует сходимость ряда с меньшими членами ;

б) из расходимости ряда с меньшими членами , следует расходимость ряда с большими членами .

II. Пусть даны два знакоположительных ряда и . Если существует конечный, отличный от 0, предел

, то ряды и сходятся или расходятся одновременно.

Задача.

Из рядов а) б) в) сходятся…

Варианты ответов: 1) только а

2) только с 3) только в и с

4) ни один не сходится 5) только в

Решение.

а) , .

,

не выполняется необходимое условие сходимости, ряд расходится.

б) , , .

Исследуем по признаку Даламбера.

, ряд расходится.

в) , .

Исследуем по признаку сравнения.

Сравним с рядом , .

Он сходится, как обобщенный гармонический ряд.

.

Значит, ряды и одновременно сходятся.

Ответ. №2.

§4 Знакочередующиеся ряды ,

8. Достаточный признак сходимости (признак Лейбница)

Знакочередующийся ряд сходится, если:

1) последовательность абсолютных величин ряда монотонно убывает, т.е. ;

2) общий член ряда стремится к нулю: .

При этом сумма ряда удовлетворяет неравенствам

.

Задача.

Установите соответствие между видами сходимости и знакочередующимися рядами.

1. абсолютно сходится А)

2. условно сходится В)

3. расходится С)

Решение.

А) , .

, ряд расходится.

9. Абсолютно сходящийся ряд

10. Условно сходящийся ряд

Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.

Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

В) , .

а) ряд сходится по признаку Лейбница.

б) ряд из модулей . Сравним с рядом , он расходится.

,

Ряд с меньшими членами расходится, значит, ряд с большими членами расходится.

Из п. а) и б) следует, что ряд - сходится условно.

С)

Ряд из модулей сходится как ряд геометрической прогрессии, значит, ряд сходится абсолютно.

Ответ. , ,

§5 Функциональные ряды

11. Ряд, членами которого являются функции от х, называется функциональным.

12. Область сходимости

Совокупность числовых значений аргумента х, при которых функциональный ряд сходится, называется областью сходимости.

13. Степенные ряды

Ряд, членами которого являются степенные функции аргумента х, называется степенным рядом.

14. Радиус сходимости степенного ряда.

15. Интервал сходимости степенного ряда

Радиус сходимости вычисляется по формулам:

Для ряда :

Для ряда :

Задача.

Радиус сходимости степенного ряда равен 10, тогда интервал сходимости имеет вид…

Варианты ответов: 1)

2) 3) 4)

Решение.

Так как , то , , .

Ответ. №1.

§6 Ряды Тейлора и Маклорена

16. Разложение функции в ряд Тейлора

Если функция бесконечно дифференцируема в окрестности точки и , то

Задача.

Если , то коэффициент разложения данной функции по степеням равен…

Варианты ответов: 1) 3 2) 0 3) 1 4) 0,25

Решение.

В разложении функции в ряд Тейлора .

В нашем случае:

, , ,

, , .

Ответ. №2.

17. Разложение функции в ряд Маклорена

Если функция бесконечно дифференцируема в окрестности точки и , то

18. Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)

,

,

,

,

,

,

,

,

,

,

Задача.

Дана функция , тогда первые три (отличные от нуля) члена разложения этой функции в ряд Тейлора в окрестности точки имеют вид…

Варианты ответов:

1) 2)

3) 4)

Решение.

Так как

, то

Ответ. №4.