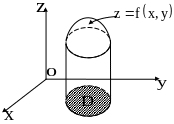- •Глава 14. Двойной интеграл
- •Глава 15. Криволинейный интеграл
- •Глава 16. Обыкновенные дифференциальные уравнения
- •Глава 17. Дифференциальные уравнения в частных производных
- •Глава 18. Ряды
- •Глава 19. Гармонический анализ
- •Глава 20. Теория поля
- •Глава 21. Теория функции комплексного переменного
- •Глава 22. Интерполирование
- •Глава 23. Численные методы
- •Глава 24. Дискретная математика
- •Глава 25. Теория вероятностей
Глава 14. Двойной интеграл
1. Вычисление двойного интеграла в декартовой системе координат |
|
а)
|
б)
|
Пусть
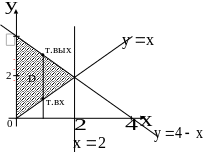
Варианты ответов: 1) прямоугольной трапеции 2) произвольной трапеции 3) треугольника 4) равнобокой трапеции Решение.
Построим фигуру,
ограниченную линиями
Область интегрирования данного интеграла имеет вид треугольника. Ответ. №3.
Задача.
Вычислить
Варианты ответов:
1)
Р Область - прямоугольник, изображенный на рисунке.
Ответ. №5. |
2. Вычисление двойного интеграла в полярной системе координат |
|
Переход к полярным
координатам полезен, когда подынтегральная
функция имеет вид
|
Задача.
Дан интеграл
Варианты ответов:
1)
2)
4)
Решение.
Так как
в полярной системе
координат будет иметь вид
Тогда
Ответ. №4. |
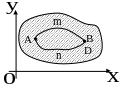
3. Приложения двойного интеграла |
|
Площадь плоской фигуры в декартовой системе координат
|
Площадь плоской фигуры в полярной системе координат
|
Объем тела
где
|
Масса плоской фигуры
где
|
Задача.
Площадь области,
ограниченная линиями
Варианты ответов:
1)
Решение.
Построим фигуру,
ограниченную данными линиями.
Ответ. №3. |
Глава 15. Криволинейный интеграл
|
Кривая задана уравнением |
|
1. Вычисление криволинейного интеграла I рода в декартовой системе координат |
|
|
|
|
|
2. Вычисление криволинейного интеграла I рода в полярной системе координат |
|
|
3. Вычисление криволинейного интеграла I рода в параметрическом виде |
|
|
4. Вычисление криволинейного интеграла II рода в декартовой системе координат |
|
|
|
|
|
5. Вычисление криволинейного интеграла II рода в параметрическом виде |
, , |
|
6. Формула Грина
|
|
Если функции
где
|
||||
7. Условия независимости криволинейного интеграла II рода от пути интегрирования
|
|
Пусть А и В – произвольные точки области D,
Тогда следующие условия равносильны:
1)
2)
3)
4)
|
||||
8. Связь между криволинейными интегралами I и II рода |
|
|
||||
9. Приложения криволинейного интеграла |
Первого рода |
Второго рода |
||||
Длина кривой |
|
Работа под
воздействием силы
|
|
|||
Масса кривой
с плотностью
|
|
Площадь плоской
фигуры, расположенной в плоскости
|
|
|||
Задача. Криволинейный
интеграл
Варианты ответов: 1) 2 2) 0 3) 4 4) 5 Решение.
Значит,
Ответ. №2.
|
||||||


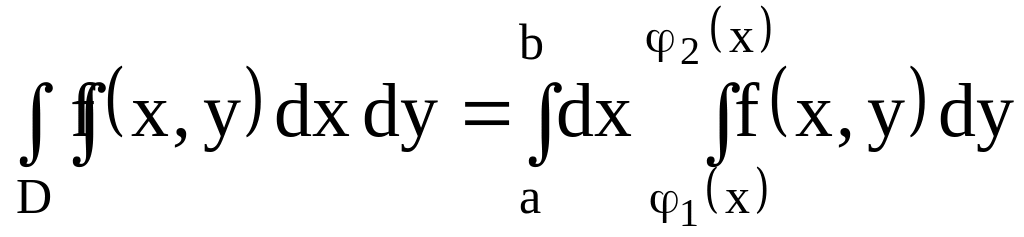

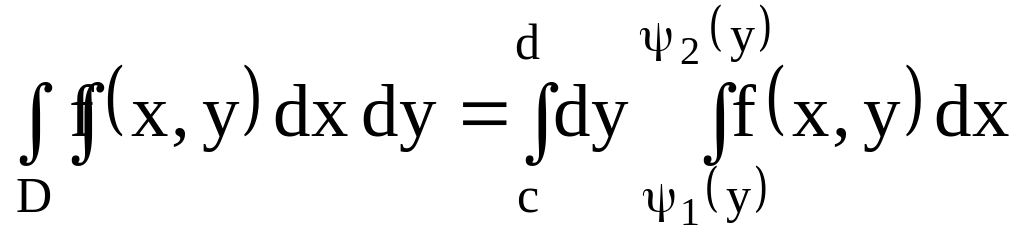
 Задача.
Задача.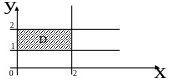 ешение.
ешение.