4.6.2.Теплообмен в термическом начальном участке круглой трубы

Будем по-прежнему полагать течение гидродинамически стабилизированным, а теплообмен осесимметричным. Тогда исходным дифференциальным уравнением энергии будет следующее:

(4.62)

Предположение о гидродинамически стабилизированном профиле скорости, конечно, является сильным упрощением, так как на начальном участке устанавливается не только профиль температуры, но и профиль скорости. Однако, в противном случае, задача не подаётся решению, так как нужно будет дополнительно решать уравнения движения.

Приведём (4.62) к безразмерному виду, для чего введём новые переменные:

где t₀ – однородная температура жидкости во входном сечении трубы.

Подставляя эти безразмерные переменные в уравнение (4.62), получаем

(4.63)

Последним слагаемым правой части уравнения учитывают перенос теплоты теплопроводностью вдоль оси трубы. Обычно полагают, что это слагаемое при RePr > 100 можно отбросить без большого ущерба для точности решения задачи.

В безразмерных переменных параболический профиль скорости стабилизированного ламинарного течения имеет вид:

u⁺ = 2 [1 – (r⁺)²].

Тогда вместо (4.63) получаем окончательную форму дифференциального уравнения энергии:

(4.63,а)

при граничных условиях

(0, r⁺) = 1; (x⁺, 1) = 0.

Плотность теплового потока на стенке в произвольном сечении x⁺ можно определить по наклону температурной кривой у стенки

Зависимость местного значения средней массовой температуры газа (жидкости) от x⁺ можно установить двумя методами: интегрированием температуры по радиусу трубы согласно (4.49) или интегрированием q_c(x⁺) от 0 до x⁺ с использованием уравнения теплового баланса _ж(x⁺) = (t_c – t_ж)/(t_c – t₀). рассмотрим второй метод подробнее.

С одной стороны, за счёт движения со скоростью V₀ в трубе радиусом R среда переносит количество теплоты, равное

Q = R²V₀ c_p(t_ж – t₀).

С другой стороны, это же количество теплоты можно выразить через изменение плотности теплового потока на стенке от входа в канал до сечения x⁺

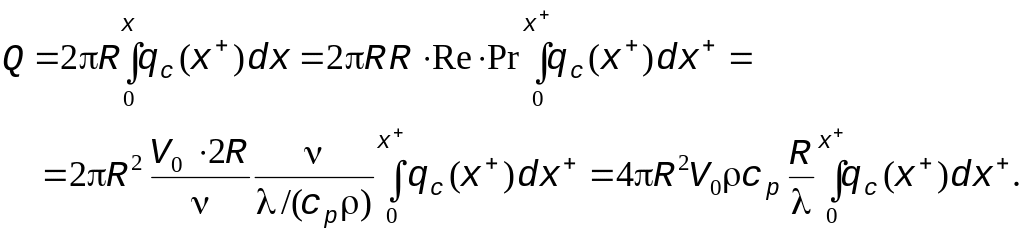
Таким образом,

Вычисляем локальный коэффициент теплоотдачи _x с учётом того что q_c(x⁺) = = _x (t_ж - t_c) =  _x(t_c – t₀)_ж(x⁺) и локальное число Нуссельта

(4.64)

При указанных граничных условиях у стенки во входном сечении gradt = , следовательно, Nu_x = . Можно ожидать, что в сечениях, удалённых от входа в трубу, число Нуссельта стремится к значению, характерному для стабилизированного теплообмена, т.е. уменьшается.

При расчётах теплообменников пользуются осреднёнными по длине трубы коэффициентами теплоотдачи. Поэтому для практики больший интерес представляет среднее число Нуссельта:

(4.65)

Приступим к решению уравнения (4.63,а) при указанных граничных условиях. Воспользуемся методом разделения переменных. Подставив в (4.63,а) (r⁺, x⁺) = = (r⁺)X(x⁺), находим

откуда получаем два раздельных ОДУ:

(4.66,а)

(4.66,б)

где  - собственное число задачи, подлежащее определению.

Первому из уравнений (4.66) удовлетворяет простая экспоненциальная функция

X(x⁺) = C exp( ²x⁺).

Решение второго уравнения, удовлетворяющее граничным условиям, может быть получено для бесконечного числа различных значений  как численными, так и приближёнными аналитическими методами. Это уравнение Штурма-Лиувилля весьма обстоятельно изученное в математической литературе. Для нас важно, что решение этого уравнения известно. Окончательное решение имеет вид:

(4.67)

где _n – собственные функции уравнения Штурма-Лиувилля, С_n – коэффициенты ряда Фурье-Штурма.

Дифференцируя (4.67) по r⁺ и приравнивая r⁺ единице, находим

(4.68)

где Интегрируя теперь (4.68) от 0 до x⁺, вычисляем безразмерную среднюю массовую температуру среды

(4.69)

Воспользовавшись уравнениями (4.64) и (4.65), легко определить локальное и среднее число Нуссельта

(4.70)

(4.71)

Как уже отмечалось, все свойства и параметры задачи Штурма-Лиувилля известны. Ниже для облегчения расчётов представлены собственные значения _n и коэффициенты ряда G_n задачи теплообмена при ламинарном течении в круглой трубе:

n 0 1 2 3 4

_n² 7,316 44,62 113,8 215,2 348,5

G_n 0,749 0,544 0,463 0,414 0,382

При n > 2 _n = 4n + 8/3,

Так как решение задачи имеет универсальный характер, то распределение температур и чисел Нуссельта по длине начального участка трубы можно рассчитать раз и навсегда. При постоянной температуре стенки имеем

x⁺ 0 0,001 0,004 0,010 0,040 0,080 0,100 0,200 

Nu_x  12,86 7,91 5,99 4,18 3,79 3,71 3,66 3,66

Nu  22,96 12,59 8,99 5,87 4,89 4,66 4,16 3,66

_ж 1,00 0,956 0,904 0,836 0,626 0,457 0,394 0,190 0,0

При больших значениях x⁺ ряды в выражениях (4.70) и (4.71) быстро сходятся. Уже при x⁺ > 0,1 расчёты можно проводить, оставляя лишь первое слагаемое ряда. При этом уравнение (4.70) принимает вид

Nu_x =

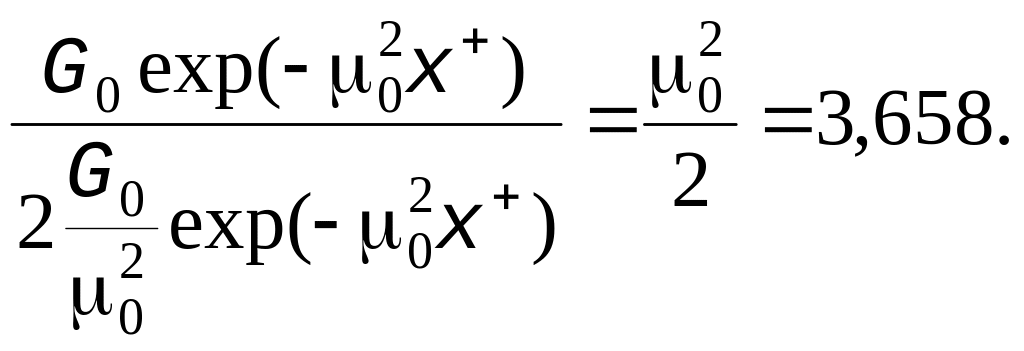
Это значение соответствует числу Нуссельта для развитого профиля температур. Таким образом, для безразмерной длины термического начального участка получаем соотношение

Тогда (x_н/D)  0,05 RePr. (4.72)

Например, (x_н/D)  17,5 при ламинарном течении воздуха (Pr = 0,7) с Re = 500. Но при движении с тем же числом Рейнольдса масла (Pr = 100) (x_н/D)  2500. Следовательно, в масляных теплообменниках стабилизированный профиль температуры достигается в очень редких случаях Поэтому рассмотренные ранее решения для развитого профиля температуры при высоких числах Прандтля малопригодны.

Аналогичным образом решается задача конвективного теплообмена на начальном участке при ламинарном течении и постоянной плотности теплового потока на стенке. В этом случае решение задачи для локального числа Нуссельта принимает вид

Nu_x = (4.73)

где Nu_ = 4,364. Собственные числа этой задачи _i² и коэффициенты ряда A_i , как и ранее, известны и равны

i 1 2 3 4 5 При i > 4 _i = 4i + 4/3;

_i² 25,68 83,86 174,2 296,5 450,9 A_i = 0,358_i^-2,32 .

A_i10³ 7,630 2,058 0,901 0,487 0,297

Соответственно изменяется и распределение локального числа Нуссельта по длине начального участка

x⁺ 0 0,002 0,004 0,010 0,020 0,040 0,100 

Nu_x  12,0 9,93 7,49 6,14 5,19 4,51 4,364