4.6. Конвективный теплообмен при вынужденном движении теплоносителя

Различают два типа конвективного теплообмена при вынужденном движении теплоноситель – в трубах (каналах) и при внешнем обтекании тел.

Ранее уже отмечалось, что размеры динамического и теплового пограничных слоёв непрерывно изменяются по мере продвижения потока вдоль омываемой им стенки. При движении газов (жидкостей) в трубах или каналах максимальный размер гидродинамического или теплового пограничных слоёв лимитируется радиусом трубы (канала). Поэтому по длине трубы выделяют гидродинамический начальный участок или участок стабилизации, в пределах которого пограничные слои формируются независимо друг от друга, и область полностью развитого течения (основной участок), где пограничные слои от противоположных стенок сомкнулись на оси трубы и более не изменяются. В области развитого или, как ещё говорят, стабилизированного течения устанавливается неизменный профиль скорости, уравнение которого определяется геометрией канала и режимом течения.

При внешнем обтекании тел размеры пограничных слоёв сверху неограниченны или, точнее говоря, ограничены длиной поверхности. Однако здесь проявляется другая особенность течения – отрыв пограничного слоя. Естественно, все расчётные методики справедливы лишь до точки отрыва пограничного слоя.

4.6.1. Аналитические решения задачи конвективного теплообмена в каналах

Ранее было приведено дифференциальное уравнение энергии для случая движения газа (жидкости) с умеренными скоростями. В цилиндрической системе координат это уравнение имеет вид:

(4.47)

Здесь ось x совпадает с осью трубы, а  - угловая координата по окружности поперечного сечения.

С целью выяснения физики процесса ограничимся сначала рассмотрением гидродинамически стабилизированного течения (v_r = 0) и осесимметричного теплообмена (²t/²) = 0. Тогда уравнение (4.47) упрощается:

(4.48)

Если пренебречь аксиальной теплопроводностью в сравнении с радиальной, то ²t/x²  0, и получаем следующее уравнение энергии для ламинарного течения в круглой трубе:

(4.48,а)

Рассмотрим сначала решения этого уравнения для случая полностью развитого ламинарного течения, когда в потоке газа (жидкости) устанавливается полностью развитый профиль температуры в сечениях, удалённых от входа в трубу. Существование такого профиля труднее наглядно продемонстрировать, чем полностью развитый профиль скорости. Однако для некоторых способов обогрева стенки в трубе устанавливается безразмерный профиль температуры по сечению, не изменяющийся по длине трубы (рис. 4.4). На этом рисунке t_ж среднемассовая (или, как её ещё называют, средняя калориметрическая) температура жидкости, определяемая из выражения:

(4.49)

где V₀ – средняя скорость движения газа (жидкости) в трубе, а R – радиус трубы.

Рис. 4.4. Безразмерный профиль температур в сечении канала по длине трубы

Если безразмерную температуру среды выразить через среднюю массовую температуру t_ж и температуру стенки трубы t_с (см. рис. 4.4), и если эта безразмерная температура не изменяется вдоль потока, то можно записать следующее уравнение, определяющее теплоотдачу на стенке

Плотность теплового потока на стенке запишем в виде произведения коэффициента теплоотдачи и разности температур стенки и средней массовой температуры газа (жидкости):

q_с = (t_с – t_ж). (4.50)

Заметим, что коэффициент теплоотдачи в этом уравнении отнесён к разности температур стенки и средней массовой температуры газа (жидкости). Такое определение  произвольно, но очень удобно.

На стенке трубы независимо от режима движения среды должно выполняться также следующее условие

q_с =  (t/r)_{r = R}.

Из трёх последних уравнений следует, что

В экспериментальных работах неоднократно отмечалось, что вдали от входа в трубу при определённых граничных условиях коэффициент теплоотдачи постоянен (по крайней мере, приближённо) и безразмерный профиль температуры не изменяется по длине трубы. Поэтому при расчётах теплообменников в большинстве случаев считают коэффициент теплоотдачи постоянным.

Условие инвариантности профиля температуры по координате x можно выразить в виде

Выполняя дифференцирование (все температуры изменяются по координате x) и разрешая результат дифференцирования относительно t/x, получаем

(4.51)

Подставляя выражение t/x из (4.51) в уравнение энергии (4.48,а), видим, что по меньшей мере для двух типов граничных условий уравнение энергии можно непосредственно проинтегрировать по r, т.е. оперировать с ним, как с обыкновенным дифференциальным уравнением (ОДУ). Рассмотрим эти условия.

Первое из них связано с постоянством плотности теплового потока на стенке. Если q_с = (t_с – t_ж) = const, то в силу того, что  = const получаем t_с – t_ж = = const. Следовательно,

(4.52,а)

Второе условие связано с постоянством температуры стенки. В этом случае t_c/x = 0, и из (4.51) находим

(4.52,б)

а) Постоянная плотность теплового потока на стенке

Как известно из курса механики жидкости и газа, уравнение профиля скорости при гидродинамически стабилизированном течении в круглой трубе представляет собой квадратичную параболу

(4.53)

Тогда уравнение энергии принимает вид

(4.54)

при граничных условиях:

(4.55)

Выполним интегрирование (4.54):

где С₁ – постоянная интегрирования. Но по первому граничному условию при r =0 t/r = 0, т.е. С₁ = 0, и второе интегрирование даёт

Из второго граничного условия находим вторую постоянную интегрирования

Таким образом, для профиля температуры газа (жидкости) в трубе окончательно имеем

(4.56)

Заметим, что средняя массовая температура пока не определена. Тем не менее, мы можем её вычислить по выражению (4.49):

(4.57)

Плотность теплового потока на стенке согласно (4.56) равна

(4.58)

Тогда

(4.59)

где D = 2R – диаметр трубы.

Как видим, выражение для  оказалось сравнительно простым. Использовав коэффициент теплоотдачи, можно записать решение в компактной форме, так как оно не зависит от абсолютных значений температур, а величина q_c прямо пропорциональна температурному напору.

В безразмерном виде уравнение (4.59) можно записать так:

(4.59,а)

б) Постоянная температура стенки

Перепишем уравнение энергии с учётом соотношения (4.52,б):

(4.60)

Граничные условия несколько упростились:

t/r = 0 при r = 0; t = t_c = const при r = R.

Нетрудно заметить, что уравнение (4.60) не поддаётся непосредственному интегрированию, так как неизвестная температура входит в обе его части. Это уравнение можно решить методом последовательных приближений. Используя в качестве первого приближения для вычисления (t_c – t)/(t_c – t_ж) выражения (4.56) и (4.57), получаем

(4.60,а)

Поскольку правая часть этого выражения представляет собой полином от r, его можно дважды проинтегрировать и, воспользовавшись граничными условиями, найти новый профиль температуры. На основании этого профиля вычисляют t_ж, q_c,  и затем Nu. Используя второе приближение профиля температуры, весь цикл расчётов повторяют и так до тех пор, пока результирующее значение числа Нуссельта с заданной точностью не достигнет предела. Выполнив несколько итераций (в данном случае достаточно трёх), легко убедиться, что установившееся значение Nu = 3,658. Это значение на 16 % меньше числа Nu при постоянной плотности теплового потока на стенке, что объясняется несколько иной формой безразмерных профилей температуры. Следовательно, коэффициент теплоотдачи до некоторой степени зависит от характера изменения температуры потока и поверхности.

Аналогичным образом анализируют теплообмен при полностью развитом ламинарном течении в каналах любой (не только круглой) формы: лишь бы возможно было получить выражение для профиля скорости.

На практике часто плотность теплового потока изменяется по окружности трубы – это типично для тепловой работы трубчатых рекуперативных теплообменников. Это обстоятельство может привести к появлению, так называемых, "горячих пятен" на поверхности трубы и, как следствие, к её прогару. Теплообмен при полностью развитом ламинарном течении в круглой трубе и постоянной плотности теплового потока, но при его произвольном изменении по окружности рассчитывается на основе решения дифференциального уравнения

при соответствующих граничных условиях. Мы не будем здесь останавливаться на методике получения решения (ниже подробно анализируется однотипная задача); отметим только, что при граничном условии

местное число Нуссельта оказывается равным

(4.61)

Если b = 0, число Нуссельта не зависит от  и, как и следовало ожидать, равно 4,364. В зависимости от значения b Nu может изменяться самым необычным образом. Например, если b = 0,458, то при  =  число Нуссельта стремится к бесконечности. При b > 0,458 Nu может стать и отрицательным. В качестве иллюстрации этого положения на рис. 4.5 представлена зависимость Nu() для случая b = 0,6.

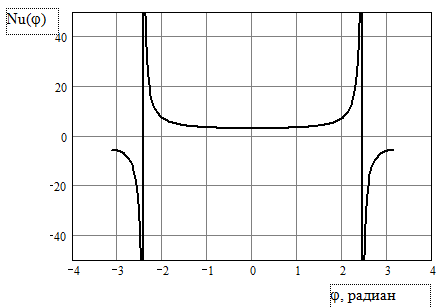
Рис. 4.5. Зависимость Nu() при несимметричном течении в трубе

Легко видеть, что здесь возникает разрыв непрерывности функции Nu() при значениях углов  = =  140^о. Эти результаты не должны вызывать недоумения, так как они являются следствием самого определения числа Нуссельта. Действительно, в Nu входит коэффициент теплоотдачи, представляющий собой отношение плотности теплового потока на стенке к разности температур стенки и средней массовой потока: Nu = = D/,  = q_c/(t_c – t_ж). Бесконечный коэффициент теплоотдачи означает просто, что температура стенки равна средней массовой температуре газа (жидкости). Поэтому бесконечное значение  не приводит к бесконечному значению q_c. Соответственно, знак "минус" обусловлен тем, что теплота передаётся от среды к стенке, а не наоборот. Но результаты рис. 4.5 со всей определённостью свидетельствуют о том, что само понятие коэффициента теплоотдачи не имеет физического обоснования, это – просто удобный для расчётов коэффициент пропорциональности (да и то не во всех случаях).