4.5.2. Использование интегрального метода

Данная задача очень удобна для иллюстрации возможностей интегрального уравнения пограничного слоя Г.Н. Кружилина.

Снова рассмотрим физическую ситуацию вблизи вертикальной стенки (рис. 4.3). Используем на этот раз для решения задачи интегральный метод

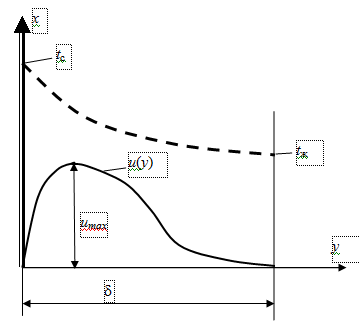
Рис. 4.3. Температурное поле вблизи поверхности стенки

Для установившегося движения среды вдоль стенки интегральное уравнение импульсов Т. Кармана имеет вид

где U – скорость невозмущённого потока, ₀ – касательное напряжение на стенке

Интегральное уравнение тепловых потоков Г.Н. Кружилина мы выводили раньше

В задаче свободной конвекции здесь имеется две особенности: во-первых, на удалении от стенки газ неподвижен, т.е. U = 0 и, во-вторых, в правой части уравнения импульсов необходимо учесть подъёмную силу g(t_c – t_ж). В любом случае для решения задачи необходимо располагать профилями относительной температуры  = t – t_ж и скорости u. Профиль температуры должен удовлетворять двум условиям: на стенке он должен обеспечивать относительную температуру (0) = _с = t_c –  t_ж, а на внешней границе пограничного слоя (при y = ) – монотонное стремление  к нулю. Этим требованиям хорошо соответствует квадратичная парабола

(4.34)

Профиль скорости, как это видно из данных рис. 4.3, описывается более сложной функцией

(4.35)

где величина u₁ пока не определена. В соответствии с (4.35) максимальное значение скорости достигается при y = /3 и составляет u_max = (4/27)u₁. Подставим эти профили в уточнённое уравнение импульсов Кармана

(4.36)

Полагая, что h =  (в этом состоит упрощение и погрешность интегрального метода), находим

и вместо (4.36) получаем

(4.37)

Аналогично вычисляя

и вместо уравнения Кружилина получим

(4.38)

Нелинейные ОДУ, к типу которых относится система (4.37) и (4.38), решаются с использованием степенных пробных функций, поэтому будем искать неизвестные u₁ и  в виде u₁ = C₁x^m,  = C₂xⁿ. Подстановка этих соотношений в (4.37) и (4.38) даёт

(4.39)

Система (4.39) должна быть верной при любых значениях x, а это означает, что координата x вообще не должна фигурировать в этих уравнениях. Но тогда показатели степени у x в каждом из уравнений должны быть равны между собой, т.е.

откуда следует, что m = ½ и n = ¼ . В этом случае система (4.39) упрощается и принимает вид

(4.39,а)

Система (4.39,а) легко решается обычной подстановкой. В результате находим

(4.40)

(4.41)

Тогда

(4.42)

и

(4.43)

или

(4.43,а)

Тепловой поток на стенке

С другой стороны q_с = _x (t_c – t_ж) = _x_c. Отсюда _x = 2/ и

(4.44)

Для воздуха Pr = 0,733 и из (4.44) имеем

Nu_x = 0,3817 Gr_x^0,25.

Точное решение даёт коэффициент 0,3592, т.е. погрешность интегрального метода составляет в данном случае величину, равную 6,27 %. Отметим, что выражение (4.44) даёт лучшие результаты, чем распространённая справочная формула

Nu_x = A (Gr_xPr)^0,25,

в которой коэффициенты A постоянны.

Для турбулентного пограничного слоя в интегральном методе изменяются лишь выражения для профилей температур и скорости (эти профили плоские):

(4.45)

В остальном процедура решения, рассмотренная ранее, не изменяется и, если степень турбулентности не становится чрезмерной, не изменяются и уравнения Кармана и Кружилина. В итоге для интенсивности свободной конвекции на плоской стенке при турбулентном течении находим

(4.46)

Мы не будем здесь рассматривать эмпирические формулу для определения коэффициентов теплообмена при естественной конвекции в различных условиях, в частности, при конвекции в ограниченных объёмах – об этом можно прочесть в учебниках и в различной литературе. Нашей целью является освоение инженерных методик расчёта конвективного теплопереноса. Помимо уже рекомендованных источников эти вопросы хорошо изложены в книгах

1. В.М. Кэйс. Конвективный тепло- и массообмен. Пер. с англ. – М.: "Энергия", 1972. – 448 с.

2. Себиси Т., Брэдшоу П. Конвективный теплообмен. Физические основы и вычислительные методы: Пер. с англ. – М.: Мир, 1987. – 592 с.