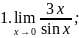Практическая работа: «Первый замечательный предел»

Цель работы: научится раскрывать неопределенность с помощью первого замечательного предела, вычислять пределы, содержащие тригонометрические функции.

Теоретическая часть:

Предел отношения синуса бесконечно малого угла к самому углу, есть величина постоянная, равная единице, т.е.

Решение одного варианта:

которую надо раскрыть с помощью первого замечательного предела:

,

Для этого умножим на множители:

используем первый замечательный предел три раза:

умножим каждую дробь на , тогда

Неопределенность вызвана присутствием корня умножим числитель и знаменатель на сопряженный множитель , тогда

в числителе свернем по формуле разность квадратов

Для раскрытия неопределенности применим первый замечательный предел: умножим на и перегруппируем множители:

умножим на сопряженный множитель и применим формулу разность квадратов:

сократим на

первую дробь умножим на , вторую на , и перегруппируем:

на множители, т.к.

в числителе в первой скобке вынесем

Практическая работа: «Первый замечательный предел»

Цель работы: научится раскрывать неопределенность с помощью первого замечательного предела, вычислять пределы, содержащие тригонометрические функции.

Вариант 1	Вариант 2

Вариант 3	Вариант 4
Вариант 5	Вариант 6

Вариант 7	Вариант 8

Практическая работа «Второй замечательный предел»

Цель работы: научиться раскрывать неопределенность вида путем применения второго замечательного предела.

Теоретическая часть:

Предел суммы единицы и бесконечно малой величины, в степени бесконечно большой, есть величина постоянная, равная числу Эйлера .

Разбор решения одного варианта:

постановка дает воспользуемся формулой второго замечательного предела, т.к. можно представить как ,

выражение в квадратных скобках равно е, тогда

постановка дает ищем формулу второго замечательного предела, т.к. то поменяв местами имеем:

в скобках выражение равно е, тогда

постановка дает воспользуемся формулой второго замечательного предела. Заметим, чтобы получилось число е, надо, чтобы степень была обратна слагаемому с «1», в нашем случае это , тогда степень должна быть , чтобы этого добиться в степени х умножим на . Перегруппируем множители, чтобы сработала формула, получим:

в степени нужно , умножим степень на , перегруппируем , тогда

, умножим на ,

перегруппируем тогда

Так как отрицательный показатель степени, отвечает за переворот дроби.

в степени нужно , для этого умножим на , перегруппируем как , тогда

тогда перегруппируем , тогда

чтобы сработала формула второго замечательного предела, нужна степень умножим на и перегруппируем

перевернем дробь, при этом степень станет отрицательной, и разделим на две дроби, тогда

второй замечательный предел: нужна степень , тогда тогда