Равносильность форм.

Пусть даны две А,В формы. Они называются равносильными, если имеют одинаковые значения при любых значениях букв, входящих в них, то есть имеют одинаковые таблицы истинности (порождают одну и ту же истинностную функцию).

Записывается А ~ В (форма А равносильна В форме).

Отношение равносильности ~ рефлексивно (А ~ А), симметрично (А ~ В, то В,~ А), транзитивно (А ~ В и В ~С, то А~С) .

Отношение равносильности разбивает множество формул на классы. Все формулы одного класса равносильны, порождают одну и ту же функцию (одна и та же таблица).

Признаком класса является таблица. Формулы разных классов не равносильны. Равносильность высказываний означает одинаковость смыслов тех высказываний, которые являются частными случаями форм.

Теорема о подстановке.

Если в некоторой форме А заменить подформу на равносильную ей формулу, то получится форма В равносильная А.

Основные законы логики высказываний:

Каждый закон представляется как равносильность двух форм.

1. Закон двойного отрицания:

2. Закон коммутативности: ,

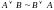
3. Ассоциативности (сочетательные):

4. 

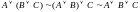
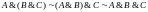
5. Дистрибутивность (распределительные):

– дистрибутивность конъюнкции,

– дистрибутивность дизъюнкции.

Эти операции взаимно дистрибутивны.

6. Законы де Моргана: .

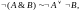
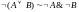7. Законы идемпотентности: , .

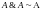8. Закон исключенного третьего: ( ).

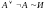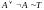9. Закон противоречия:

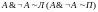
10. Законы поглощения: , , , , ,

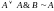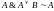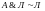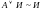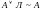
(в последних четырех формулах И можно заменить на Т, а Л – на П).

В 9 законе присутствуют только 3 операции - ¬,&,v – они главные. Не главные операции выражаются через главные.

10. Закон исключения импликации: .

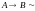
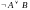11. Закон исключения эквивалентности: .

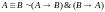Все законы являются справедливыми, если в них буквы заменить произвольными формами.

Лекция 4.

Нормальные формы.

Теорема 1.

Для любой формы существуют равносильные ей ДНФ и КНФ (дизъюнктивная нормальная форма и конъюнктивная нормальная форма).

Пусть дана форма А = А (А₁,…А_n). Переход к ДНФ.

1. Исключаем все связки, кроме ¬,&,v (законы 10, 11).

2. Вносим отрицания в скобки, то есть добиваемся «тесных» отрицаний (закон 5).

3. Раскрываем все скобки по законы дистрибутивности конъюнкций (закон 4).

4. Получаем ДНФ.

ДНФ состоит из дизъюнкций элементарных конъюнкций.

Переход к КНФ.

1. Исключаем все связки, кроме ¬,&,v (законы 10, 11).

2. Вносим отрицания в скобки, то есть добиваемся «тесных» отрицаний (закон 5).

3. Раскрываем скобки по закону дистрибутивности дизъюнкции (закон 4).

4. Получаем КНФ.

КНФ состоит из конъюнкции элементарных дизъюнкций.

Проблему выполнимости можно решить с помощью ДНФ и КНФ.

Теорема 1.

Форма выполнима, то есть не является противоречием тогда и только тогда, когда равносильная ей ДНФ содержит хотя бы одно слагаемое, в котором нет пары множителей А&¬А.

Теорема 2.

Форма не выполнима, то есть является противоречием тогда и только тогда, когда равносильная ей ДНФ в каждом слагаемом содержит пару множителей А&¬А.

А не выполнима (~П)↔ А&¬А.

Форма А является тавтологией тогда и только тогда, когда равносильная ей КНФ содержит в каждом множителе пару слагаемых вида Аv¬А.

Пример:

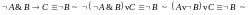
А = ~ 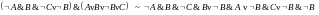– ДНФ, формула выполнима.

Из этой формулы можно получить истинные частные случаи, модель для истинных высказываний.

Для того, чтобы выяснить, при каких значениях выполняется форма нужно принять буквы с отрицанием как ложь, без отрицания – истину.

Из данного примера можно получить 5 вариантов истинны высказывания (А=Л, В=И, С=Л; В=Л). С помощью КНФ распознаем тавтологию. Так как нет пары, это не тавтология. Из этой формы можно получить и истину, и ложь. Ложные при А=И, В=И; В=И, С=И.