
- •305000, Г. Курск, ул. Радищева, 33
- •Введение
- •Глава 1. Элементы общей топологии
- •§ 1. Метрическое пространство
- •Примеры метрических пространств
- •§ 2. Определение и примеры топологических пространств
- •§ 3. Понятие подпространства. Замкнутые
- •Множества
- •Внутренние, внешние и граничные точки
- •Понятие подпространства
- •Замкнутые множества
- •Внутренние, внешние и граничные точки
- •§ 4. Базис. Аксиомы отделимости
- •Аксиома отделимости
- •§ 5. Компактность топологических пространств. Связность топологических пространств
- •Связность топологических пространств
- •§ 6. Топологические преобразования топологических пространств Непрерывные отображения
- •Примеры непрерывных отображений
- •Топологические отображения
- •Примеры гомеоморфных пространств и гомеоморфизмов
- •Глава 2. Топологические свойства поверхностей
- •§ 1. Понятие двумерного многообразия
- •§ 2. Эйлерова характеристика поверхности
- •§ 3. Ориентируемые и неориентирумые поверхности
- •Классификация замкнутых поверхностей
- •Решение нулевого варианта контрольной работы
- •Тест по курсу «геометрия-топология»
- •2 Семестр, отд. МоАис
- •Список литературы
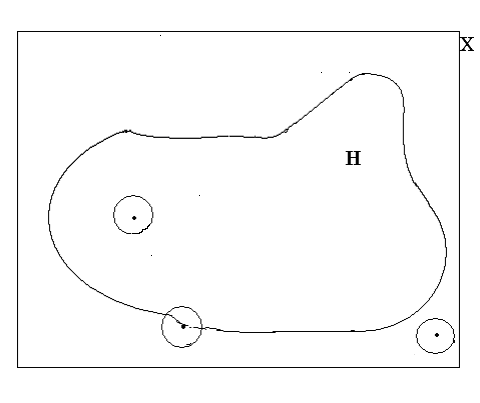
Внутренние, внешние и граничные точки
Пусть (Х, Ф) – топологическое пространство. Открытое множество U называется окрестностью точки х если х U (х X и U Ф).
Определение 4. Точка называется внутренней точкой некоторого множества H (H X), если существует такая окрестность U точки ,что U H. Множество всех внутренних точек множества H обозначается через int H и называется внутренней областью H или внутренностью H.
Определение 5. Точка называется внешней точкой множества H, если существует такая окрестность V точки , в которой нет точек из H, т.е. V Сх H=Х \ H. Множество всех внешних точек множества H обозначается через ext H и называется внешней областью H.
Определение 6. Точка с называется граничной для множеств H, если в любой окрестности точки с имеются как точки множества H, так и точки не принадлежащие H.
Множество
всех граничных точек множества H
обозначается через
![]() H
и называется границей H.
H
и называется границей H.
Очевидно:
int H ext H H = X
int H ext H = ext H H = int H =
int H = ext Cx H, ext H = int Cx H
H = Cx H
Теорема 3. Для любого множества H топологического пространства (Х, Ф) имеем
int H Ф ,ext H Ф.
H – замкнутое множество.
Доказательство.
По определению для ![]()
int
H
существует окрестность U
точки
такая, что U
H.
int
H
существует окрестность U
точки
такая, что U
H.
Поскольку открытое множество является окрестностью любой своей точки, то U int H , то есть U состоит только из внутренних точек H.
Тогда
int
H
=
![]() U
и в силу
аксиомы 2 топологического пространства
получим int
H
Ф.
U
и в силу
аксиомы 2 топологического пространства
получим int
H
Ф.
Так как ext H = int (X \ H), то получаем ext H Ф.
Так как H = X \ (int H ext H ), то H замкнуто в (Х, Ф).
Определение 7. Точка называется точкой прикосновения множества H, если каждая окрестность точки имеет с H хотя бы одну общую точку.
Множество
всех точек прикосновения множества H
называется замыканием множества H
и обозначается
![]() .
Ясно, что
= int
H
H
и является замкнутым множеством.
.
Ясно, что
= int
H
H
и является замкнутым множеством.
Определение 8. Точка H называется изолированной точкой множества H, если существует окрестность U точки , такая, что
U H =
Определение 9. Если и не является изолированной для H, то она называется предельной точкой множества H.
Ясно, что в каждой окрестности предельной точки H существуют точки множества H, отличные от .
Поскольку замыкание распадается на множество изолированных и предельных точек, а первое всегда содержится в H, то приходим к следующему утверждению:
Теорема 4. Множество H замкнуто тогда и только тогда, когда оно содержит все свои предельные точки, то есть, если
H =
Действительно, если H – замкнуто, то C H = X \ H открыто. Поэтому C H = ext H.
Отсюда получаем
H = int H ∂ H = .
Теорема 5. Если замкнутое множество F содержит множество H, то F содержит и .
Доказательство. Так как H F, то все предельные точки H будут являться предельными и для F, а поэтому они принадлежат F, следовательно
F.
Следствие. Замыкание множеств H есть пересечение всех замкнутых множеств, содержащих H.
Действительно, согласно теореме 5 принадлежит любому замкнутому множеству, содержащему H , а по теореме 3 из §3 - замкнутое множество.
Пример 1. Если (Х, Ф) – антидискретное топологическое пространство, то внутренность любого его подмножества, за исключением самого Х, пустое множество.
Если (Х, Ф) – дискретное пространство, то любое его подмножество открыто и замкнуто одновременно и, следовательно, совпадает со своей внутренностью и со своим замыканием.
Если X = R с обычной топологией, то внутренность множества всех целых чисел пустое множество.
Внутренность
множества рациональных чисел
![]() – пустое множество. Поэтому получаем,
что замыкание
– пустое множество. Поэтому получаем,
что замыкание
![]() = R,
а замыкание внутренности множества
рациональных чисел
= R,
а замыкание внутренности множества
рациональных чисел
![]() = ,
при этом int
= R.
= ,
при этом int
= R.
Таким образом, замыкание внутренности множества может сильно отличаться от внутренности замыкания.
Таким образом, оператор перехода к внутренности и оператор замыкания, вообще говоря, не коммутируют.
Если Х – антидискретно и А Х, А , то А = Х.
Если Х – дискретно и А Х, А , то А = .
Границей множества рациональных чисел, так же как и границей множества всех иррациональных чисел, служит всё множество вещественных чисел.
Пример
2. Пусть
![]() ,
,
![]() ,
,
![]() Найти
Найти
![]() и все замкнутые множества.
и все замкнутые множества.
Решение.
Рассмотрим
точку
![]() и выберем из списка открытых множеств
,
такое которое содержит точку
и выберем из списка открытых множеств
,
такое которое содержит точку
![]() и входит в
и входит в
![]() .
Очевидно,
.
Очевидно,
![]() следовательно,
следовательно,
![]() .
Для точки
.
Для точки
![]() такого открытого множества нет.
Следовательно,
такого открытого множества нет.
Следовательно,
![]() .
Точка
.
Точка
![]() и поэтому
и поэтому
![]() .
Итак окончательно получаем
.
Итак окончательно получаем
![]() .
.
![]() .
.
![]() .
Найдем
.
Найдем
![]() .
.
Рассуждая
аналогично, получаем, что
![]() .
Для точки
.
Для точки
![]() нет открытого множества содержащегося
в
нет открытого множества содержащегося
в
![]() .
Следовательно,
.
Следовательно,
![]() ,
,
![]() .
Для нахождения граничных точек
.
Для нахождения граничных точек
![]() воспользуемся формулой
воспользуемся формулой
![]() или
или
![]() .
.
![]() .
.
Напомним,
что множество называется замкнутым,
если его дополнение открыто, т.е.
![]() - замкнуто
- замкнуто
![]() .
Возьмем список открытых множеств
и, используя дополнения, составим список
замкнутых множеств
.
Возьмем список открытых множеств
и, используя дополнения, составим список
замкнутых множеств
![]() .
.
![]() .
.
Ответ:
,
,
![]() ,
.
,
.
Теорема 6. Пусть А – подмножество топологического пространства (Х, Ф). Тогда:
1)
А
=
![]()
![]() =
\ int A.
=
\ int A.
2) Х \ A = int A int (Х \ A).
3) = А А, int A = А \ А.
4) А = А А.
А = int А А А = .
Доказательство непосредственно следует из определения , int A, ext A и А.
Определение 10. Множество H называется всюду плотным в топологическом пространстве (Х, Ф), если = X.
Множество
А называется нигде не плотным в
пространстве(Х, Ф), если дополнение к
замыканию А всюду плотно в Х, то есть
![]() =
Х
=
Х
Теорема 7. Пусть H X, Ф = G
Тогда = Х H для любого .
Доказательство.
1) = Х. Тогда для произвольного открытого множества имеем .
Если х0 , то х0 . Но, согласно определению точки прикосновения, имеем
H
2) Пусть для любого : H .
Покажем, что Х . Действительно, если х0 Х и х0 H, то для любой окрестности точки х0 имеем:
H ,
а это значит, что
х0 и Х .
Так как всегда Х, то Х = .
