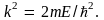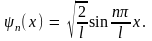10.4. Частица в одномерной потенциальной яме

Квантование энергии можно продемонстрировать на примере движения микрочастицы в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Потенциальная энергия частицы вне и внутри потенциальной ямы имеет следующие значения

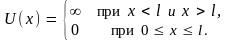
Параметр l есть ширина ямы; энергия отсчитывается от дна ямы. Уравнение Шредингера в пределах ямы (0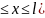 будет иметь вид

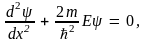
или

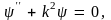(9.7)

где

(9.8)

Уравнение (9.8) имеет такой же вид, как и уравнение движения гармонического осциллятора (7.1), с той лишь разницей, что в уравнение (9.8) входит вторая производная по пространственной координате, а в уравнение движения осциллятора (7.1) – вторая производная по времени. Одинаковые уравнения имеют одинаковые решения, поэтому решение уравнения (9.8) можно записать в виде

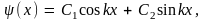
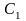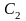где и – постоянные.

Поскольку за пределы бесконечно глубокой ямы частица проникнуть не может, то вероятность обнаружения частицы в областях x < 0 и x > l, а значит, и сама волновая функция в этих областях (за границами ямы) должны быть равны нулю. Условие непрерывности волновой функции требует, чтобы она была равна нулю и на границах ямы. Таким образом, имеем два граничных условия:

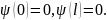(9.10)

Первое граничное условие (9.10) дает 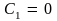и тогда 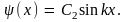Постоянную определим из условия нормировки

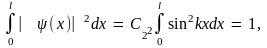
выражающее тот факт, что вероятность обнаружения частицы в пределах ямы как вероятность достоверного события равна единице. Вычислив интеграл, получим 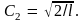С учетом этого для волновой функции частицы будем иметь

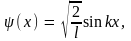
Второе граничное условие (9.10) приводит к уравнению

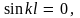
откуда получаем 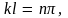где 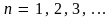– целое число (значение 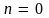исключается, так как при этом 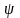было бы равна нулю при любом x, что лишено физического смысла). Подставив в формулу для волновой функции значение 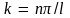, окончательно получим

(9.9)

При таких значениях параметра k из соотношения (9.9) получаем формулу для энергии частицы в потенциальной яме:

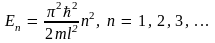(9.10)

Выражение (9.10) определяет спектр энергии (энергетический спектр) частицы в одномерной потенциальной яме; он изображен на рис. 9. Как видим, энергетический спектр является дискретным – энергия квантуется. Этот результат принципиально отличается от результата классической механики. При той же потенциальной энергии классическая частица может двигаться с любой полной энергией E > 0. Это есть периодическое движение туда и обратно между двумя потенциальными стенками – колебания между точками x₁ = 0 и x₂ = l. В квантовой механике движение возможно только с определенными дискретными значениями энергии E_n, определяемыми выражением (9.10). Другие значения энергии невозможны: вероятность обнаружения частицы внутри ямы с энергией, отличающейся от E_n, равна нулю.

Число n в (9.10) нумерует энергетический уровень частицы и называется квантовым числом. Каждому значению n отвечает определенная волновая функция 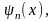определяемая формулой (9.9). Поэтому число n определяет квантовое состояние частицы в одномерной потенциальной яме. Так как каждому значению n соответствует одна волновая функция, то уровни энергии оказываются невырожденными. Наименьшее значение энергии E_min, соответствующее наименьшему значению n = 1,

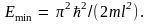
Эту энергию называют нулевой энергией. Заметим, что она не равна нулю, поэтому микрочастица в потенциальной яме ни при каких условиях не может покоиться.

Расстояние между соседними уровнями энергии

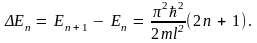(9.11)

Как видим, это расстояние увеличивается с ростом номера уровня n – уровни удаляются. При малой массе m частицы и малой ширине ямы l расстояние между соседними уровнями 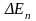велико и квантование энергии резко выражено. С увеличением m или l величина уменьшается, квантование энергии становится не заметным, а при 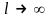независимо от массы частицы исчезает совсем 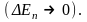Спектр энергии становится непрерывным. Это имеет место и при т.е. для макроскопических тел.

Этот пример показывает, что если движение частицы ограничено в пространстве (является финитным), то ее энергетический спектр является дискретным, а если не ограничено (инфинитно) – непрерывным. Заметим также, что в классическом пределе, когда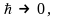 имеем 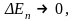т.е. спектр энергии становится непрерывным

Относительное расстояние между энергетическими уровнями

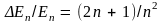
с ростом n уменьшается и при очень больших n оно становится таким малым, что распределение разрешенных значений энергии оказывается практически непрерывным.

Мы видим на рассматриваемом примере, что при больших квантовых числах квантовая механика переходит в классическую механику; поведение частицы при выполнении этого условия все более утрачивает особенности, характерные для микрочастицы. Здесь мы снова встречаемся с проявлением общего физического принципа, называемого принципом соответствия (с ним мы познакомились при изучении теории относительности).

Обратимся теперь к волновой функции микрочастицы. При n = = 1 волновая функция (9.9) примет вид

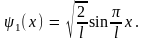
Она обращается в нуль в двух точках x₁ = 0 и x₂ = l. При n = 2 волновая функция

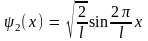(10.12)

обращается в нуль в трех точках x₁ = 0, x₂ = l/2 x₃ = l, т.е. на краях и посередине ямы. Вообще, волновая функция (10.9) имеет нули в точках, определяемых соотношением

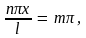
т.е. в точках с координатами

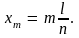
При этом число m может принимать значения 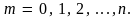В этих точках и вероятность обнаружения частицы равна нулю.

Используя волновую функцию (9.12), найдем вероятность p нахождения частицы в первой и во второй половинах ямы. Имеем:

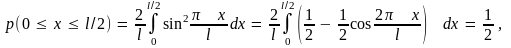
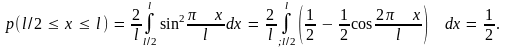
При этом волновая функция посередине ямы (в точке x = l/2) равна нулю, а значит, равна нулю и вероятность обнаружения частицы посередине ямы. Таким образом, при n = 2 частица с одинаковой вероятностью, равной 1/2, может оказаться в двух половинах ямы, не переходя через середину ямы. Этот результат невозможен с точки зрения классических представлений; он несовместим с классически представлением о движении частицы по траектории. В классическом случае частица, двигаясь от одной стенки до другой, с отличной от нуля вероятностью может оказаться в любой точке внутри ямы.