§ 91. Уравнение перпендикуляра, опущенного из данной точки на данную прямую

Уравнение перпендикуляра, опущенного из точки

на прямую, заданную каноническими уравнениями

относительно декартовой прямоугольной системы координат, можно записать в виде пересечения двух плоскостей:

,

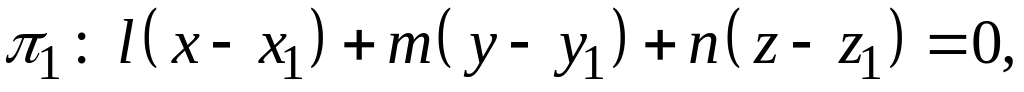
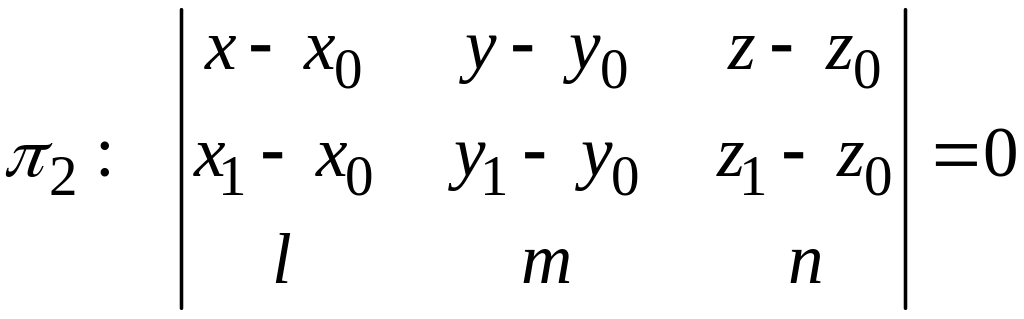т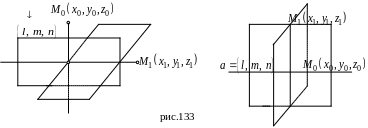 ак как первое из этих уравнений выражает плоскость, проходящую через точку перпендикулярно данной прямой, а второе – плоскость, проходящую через данную точку и данную прямую. Эти две плоскости пересекаются по прямой, проходящей через точку и пересекающей данную прямую под углом (рис. 133).

§ 92. Уравнение общего перпендикуляра к двум неколлинеарным прямым

Пусть две прямые p и q заданы своими каноническими уравнениями:

,

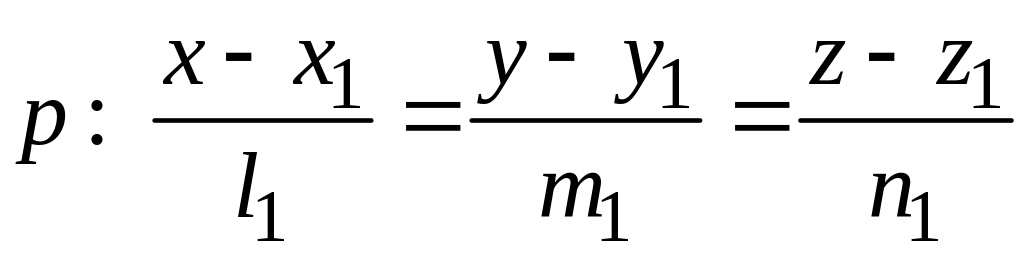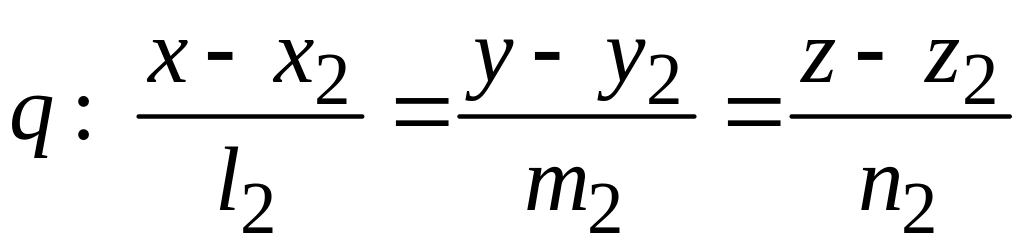
относительно декартовой прямоугольной системы координат. Предположим, что направляющие векторы этих прямых

и

неколлинеарны, т.е. что данные прямые или скрещиваются, или пересекаются. Пусть l – прямая, которая пересекает обе прямые под углом .

Тогда за направляющий вектор прямой l можно взять векторное произведение 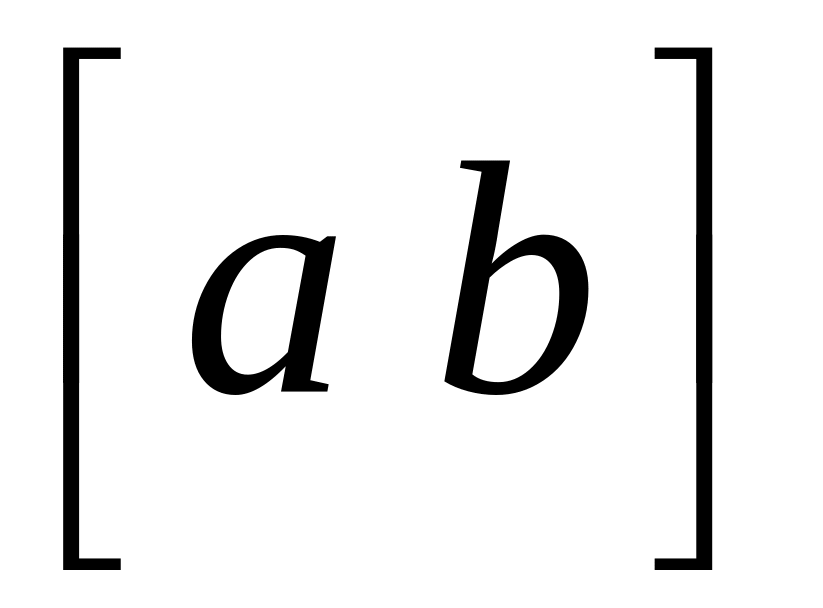направляющих векторов данных прямых:

.

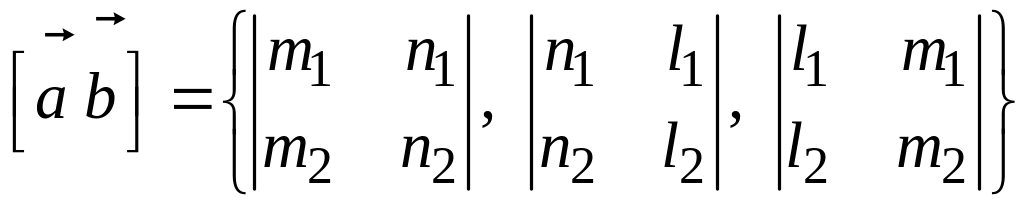Общий перпендикуляр l к двум данным прямым можно определить как прямую, по которой пересекается плоскость , проходящая через прямую р компланарно вектору , с плоскостью , проходящей через прямую q компланарно , (рис.134). Уравнение плоскости , имеет вид:

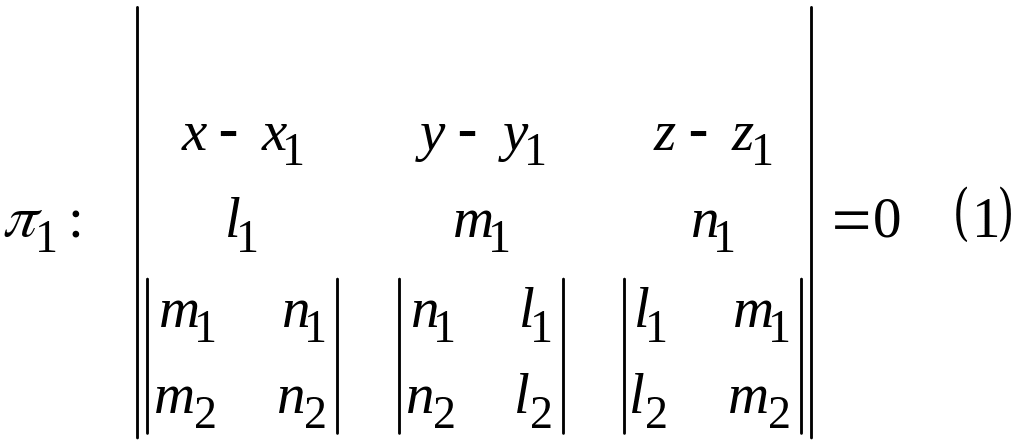
Так как эта плоскость проходит через точку прямой р, и коллинеарна векторам и .

Аналогично составляется уравнение плоскости :

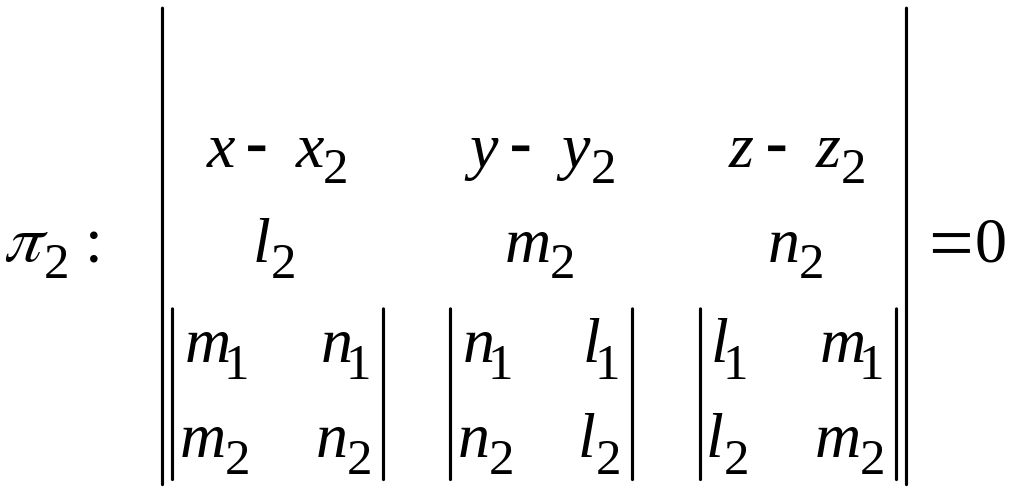. (2)

Общий перпендикуляр l к данным прямым выражается уравнениями (1) и (2).

§ 93. Расстояние от точки до прямой в пространстве

Пусть в пространстве заданы точка 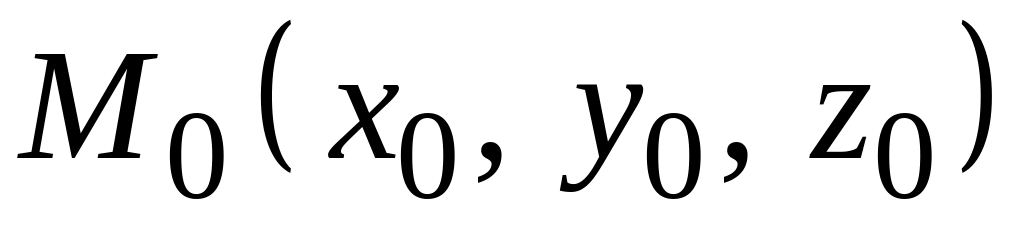и прямая l каноническими уравнениями

.

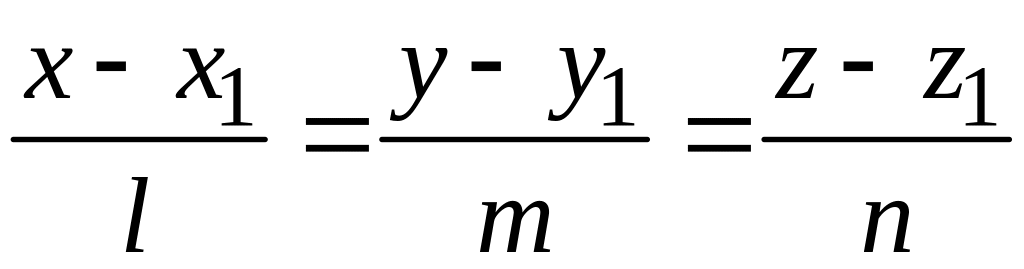относительно декартовой прямоугольной системы координат.

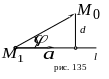Расстояние d от точки до прямой l можно определить как высоту параллелограмма, сторонами которого служит вектор и направляющий вектор прямой l отложенный от точки этой прямой. Поэтому для определения расстояния d рассмотрим модуль векторного произведения:

.

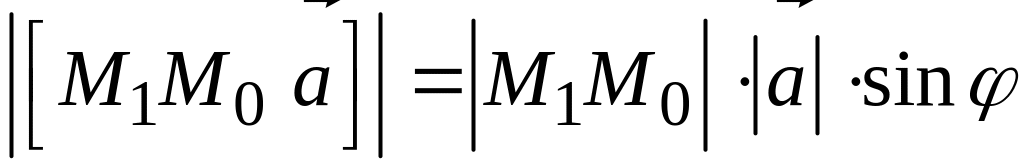Но 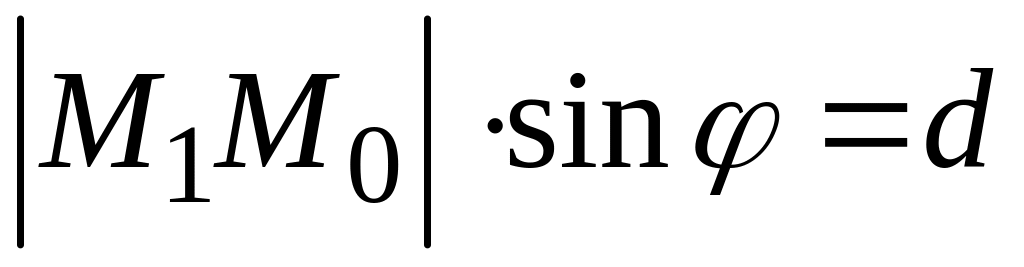, следовательно (рис. 135),

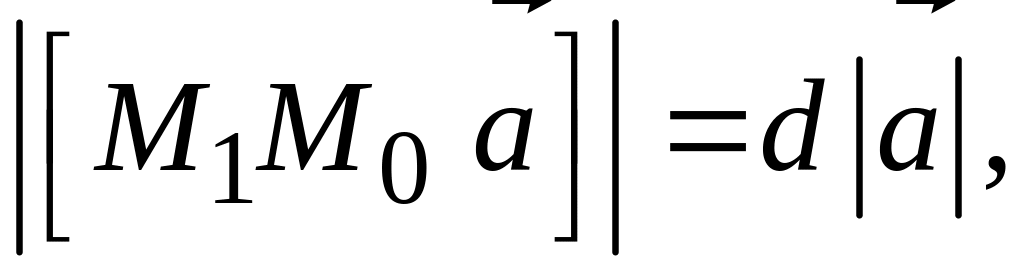
откуда .

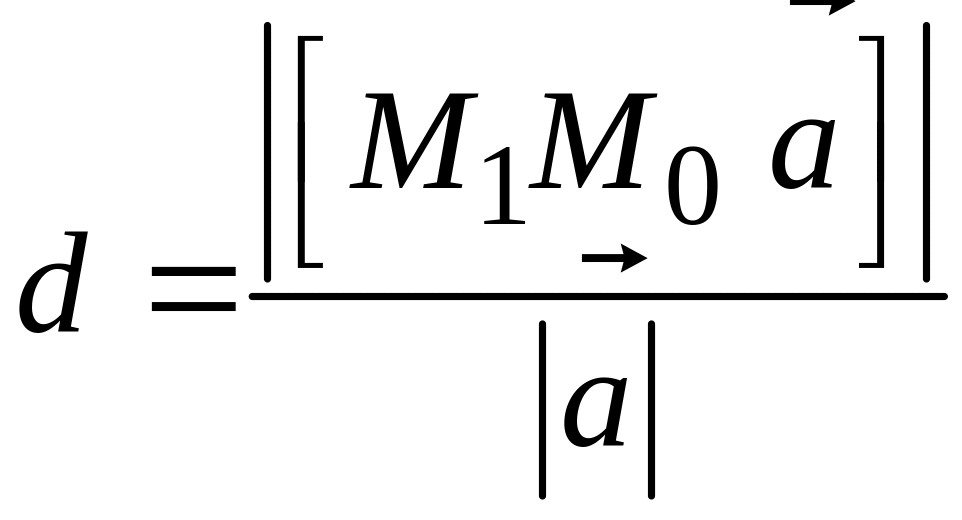Так как ,

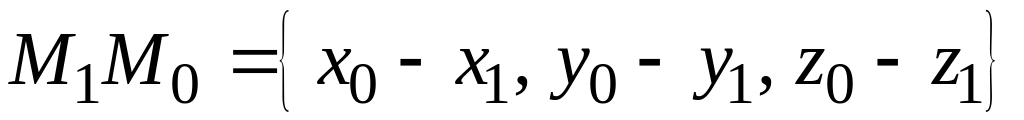то Потому

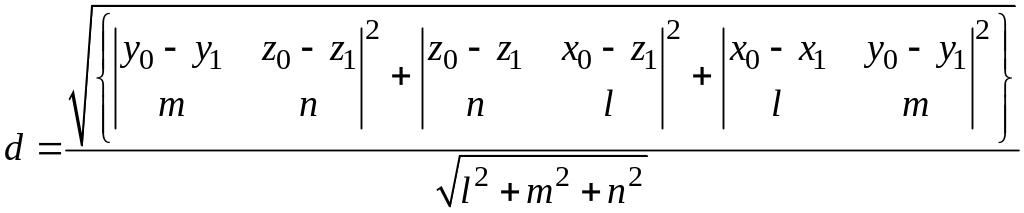
§ 94. Кротчайшее расстояние между двумя прямыми

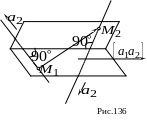
Если две прямые скрещиваются, т.е. не лежат в одной плоскости, то кротчайшее расстояние между ними (как доказывается в элементарной геометрии) есть длина отрезка общего перпендикуляра к этим двум прямым, концы которого лежат на этих прямых. Отсюда следует, что кротчайшее расстояние между двумя скрещивающимися прямыми равно величине ортогональной проекции любого отрезка концы которого лежат на этих прямых (рис. 136) на любую прямую, перпендикулярную к данным; это очевидно при проектировании точек и на общий перпендикуляр к данным прямым; величина проекции не изменится, если спроектировать отрезок на любую прямую, параллельную этому перпендикуляру. Пусть две скрещивающиеся прямые заданы каноническими уравнениями

,

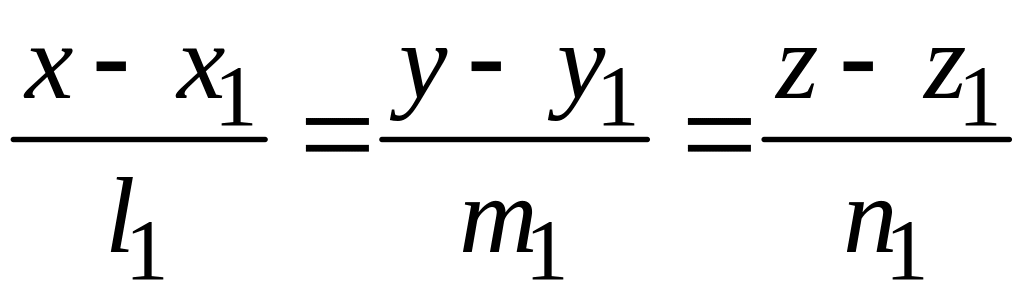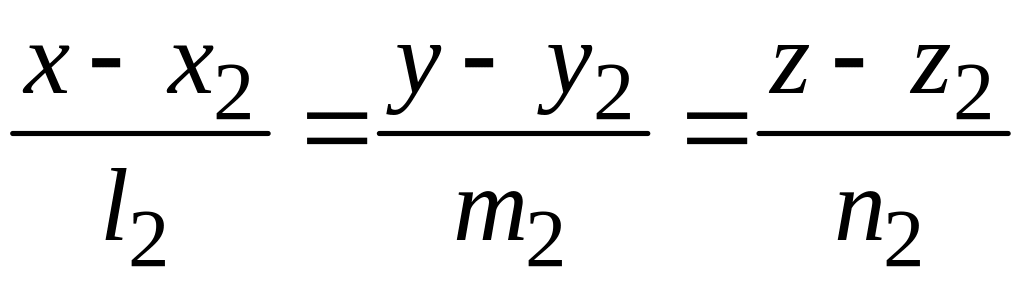
относительно декартовой прямоугольной системы координат. Кратчайшее расстояние между ними равно абсолютной величине проекции вектора

,

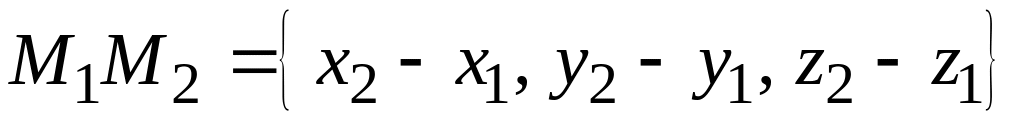начало конец которого лежат соответственно на первой и второй прямых, на прямую, параллельную вектору

,

перпендикулярному направляющим векторам:

;

данных прямых.

Так как

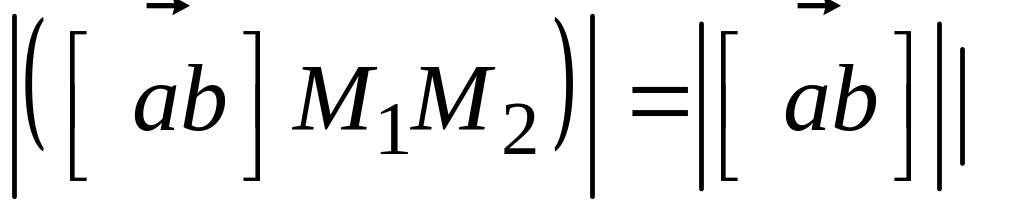пр. ,

то кротчайшее расстояние d между двумя скрещивающимися вычисляется по формуле

,

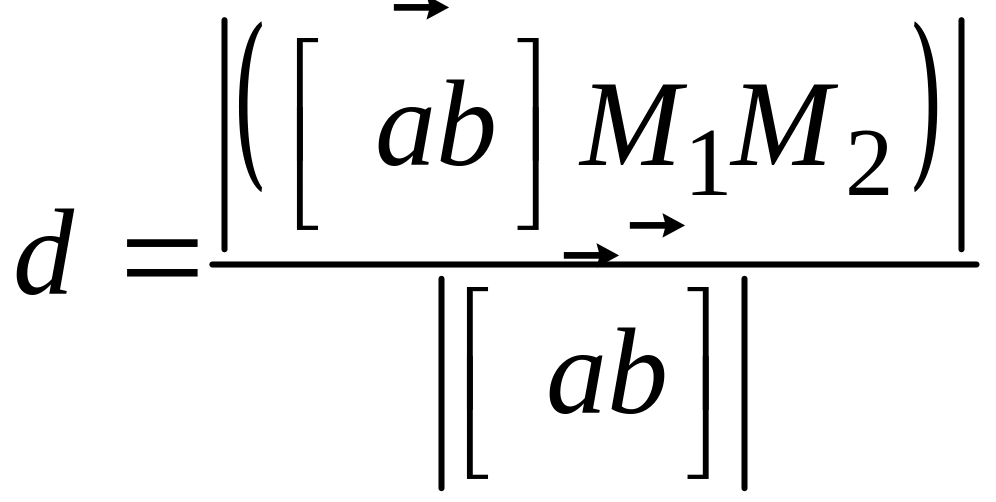или в координатах

.

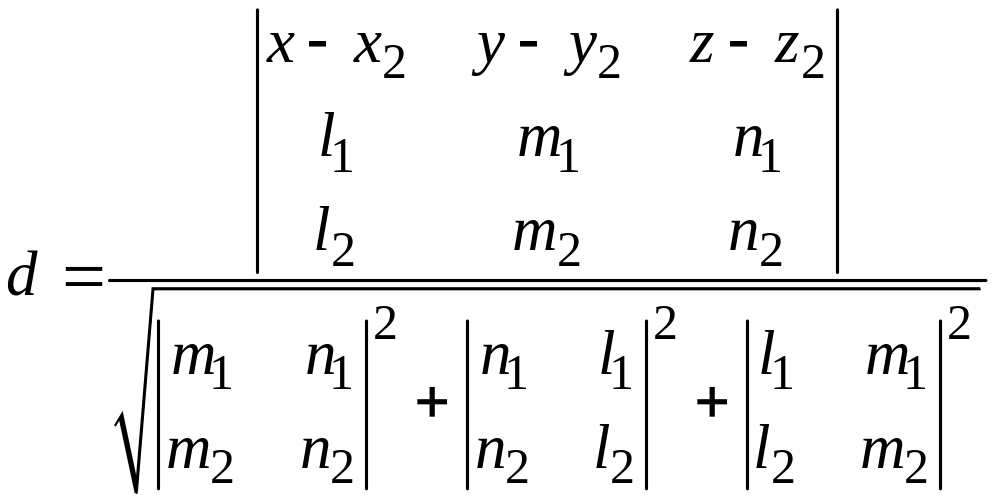Отметим, что эта формула верна и для двух пересекающихся прямых: числитель обратится в нуль, а знаменатель отличен от нуля, и мы получим d = 0 в соответствии с определением кротчайшего расстояния между двумя пересекающимися прямыми.