§ 88. Угол между двумя плоскостями. Условие перпендикулярности двух плоскостей
Косинусы углов между двумя плоскостями, заданными уравнениями (1)
(2)
относительно
декартовой прямоугольной системы
координат, выражаются формулой
.
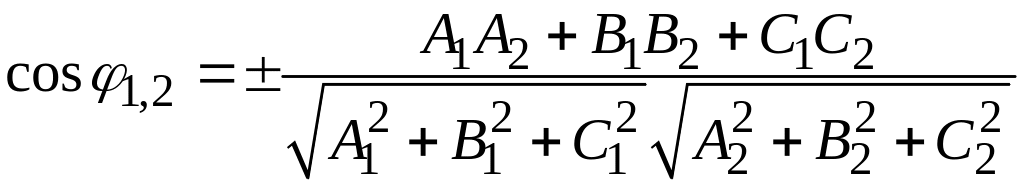(3)
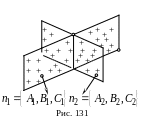Из этой формулы видно, что угол между
плоскостями определяется через угол
между векторами
и
нормальными соответственно к данным
плоскостям.
Если
формулу (3) Записать в виде (4), где перед
радикалами брать знак "плюс", то
это будет угол между плоскостями
и
,
внутренние точки которого находятся в
положительном полупространстве от
одной плоскости и в отрицательном
полупространстве от другой плоскости
(рис. 131).
.
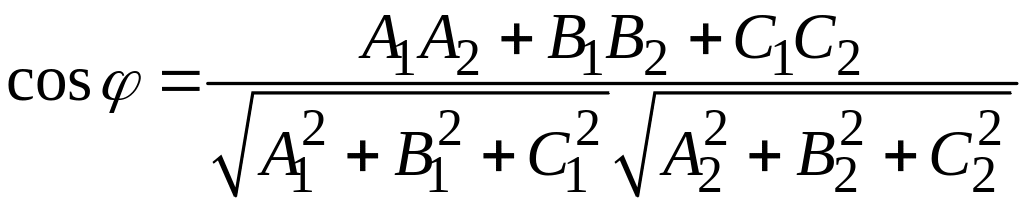(4)
Следствие. Необходимым и достаточным условием перпендикулярности двух плоскостей, заданных общими уравнениями
относительно декартовой прямоугольной системы координат, является равенство
§ 89. Угол между двумя прямыми. Условие перпендикулярности двух прямых
Углом
между двумя прямыми в пространстве
называется любой из углов между двумя
параллельными им прямыми, проходящими
через произвольную точку пространства.
Таким образом, две прямые в пространстве
(если они не перпендикулярны) образуют
между собой два различных угла: один
острый, а другой тупой. Сумма этих углов
равна
.
Пусть
и
- направляющие векторы данных прямых,
заданных относительно декартовой
прямоугольной системы координат. Угол
между этими векторами равен одному из
углов, образованных данными прямыми.
Следовательно, косинусы углов между
двумя данными прямыми выражаются
формулой:
.
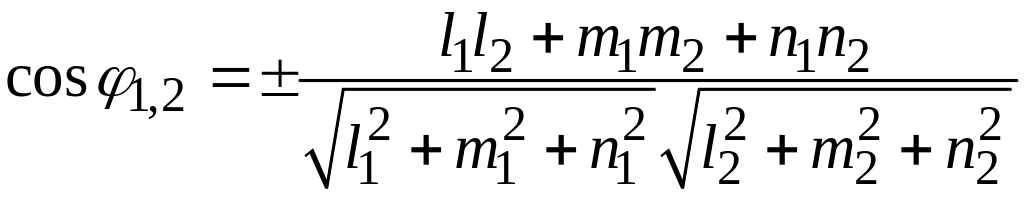Отсюда получаем необходимое и достаточное условие перпендикулярности двух прямых:
;
для того, чтобы две прямые были взаимно перпендикулярны, необходимо и достаточно, чтобы сумма произведений соответствующих векторов этих прямых была равна нулю.
§ 90. Угол между прямой и плоскостью Условие перпендикулярности прямой и плоскости
Углом
между прямой и плоскостью (если они
неперпендикулярны) называется меньший
из двух углов между этой прямой и ее
ортогональной проекцией на эту плоскость.
Если же прямая и плоскость перпендикулярны,
то угол между ними считается равным
.
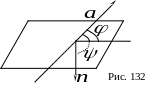Пусть относительно декартовой
прямоугольной системы координат заданы
плоскость
общим уравнением
и прямая р каноническими уравнениями
.
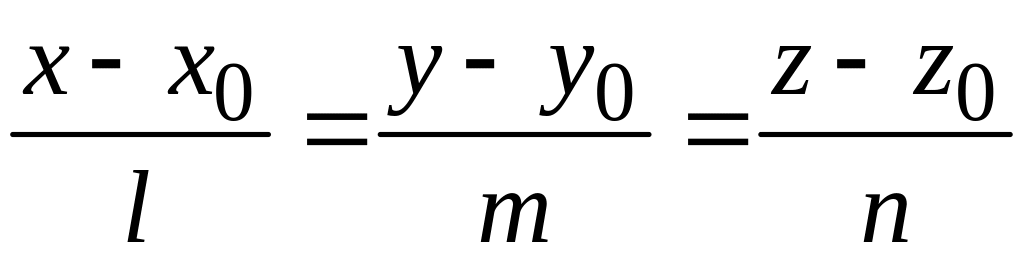Косинус
угла
между вектором
перпендикулярным данной плоскости и
направляющим вектором
данной прямой по абсолютной величине
равен синусу угла
между данной прямой и данной плоскостью
(рис. 132). Но косинус угла
между вектором
и
равен
,
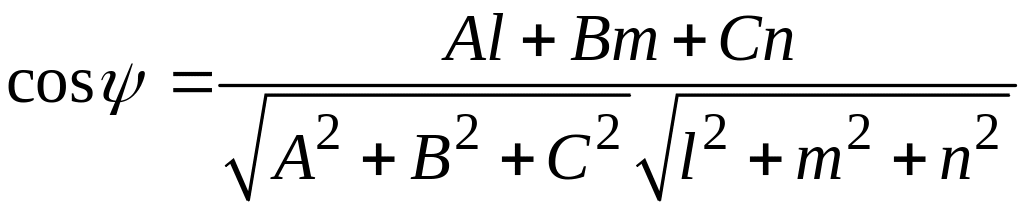следовательно, синус угла между данной прямой и данной плоскостью определится по формуле
Если прямая, заданная уравнениями , перпендикулярна плоскости
то
направляющий вектор
прямой коллинеарен вектору
,
перпендикулярному данной плоскости.
Поэтому координаты этих векторов
пропорциональны, т.е. существуют такое
отличное от нуля число
,
что
,
или
.
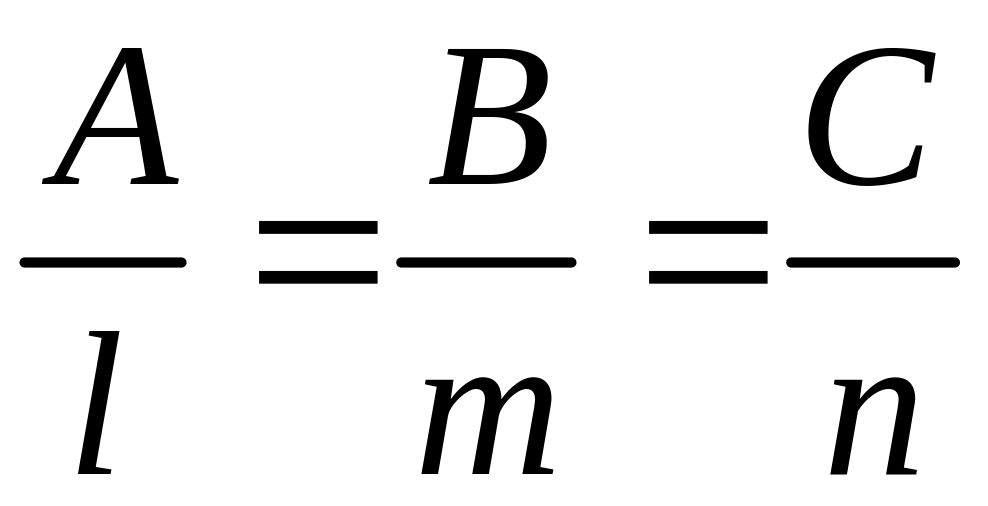Обратно, если выполнены эти соотношения, то векторы и коллинеарны, т.е. направляющий вектор данной прямой коллинеарен вектору , перпендикулярному данной плоскости, следовательно, данная прямая и плоскость взаимно перпендикулярны.
Итак, для того чтобы прямая и плоскость, заданная относительно декартовой прямоугольной системы координат, были перпендикулярны, необходимо и достаточно, чтобы координаты направляющего вектора прямой были пропорциональны коэффициентам при х, у, z в уравнении плоскости.
Клетеник № 976: № 977; № 975.