VIII. Четырехугольники

VIII.1. Теоретическая карта №8

VIII.1.1. Четырехугольники и площади

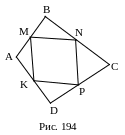1. Рис. 194.

ABCD – четырехугольник,

M, N, P, K – середины его сторон, тогда

1.1. MNPK – параллелограмм.

1.2. .

2. 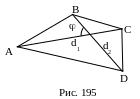Рис. 195.

ABCD – четырехугольник,

АС, BD – его диагонали,

АС=d₁, BD=d₂, тогда

.

Если φ=90°, например, ромб (квадрат), то

.

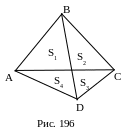
3. Рис. 196.

ABCD – четырехугольник,

АС, BD – его диагонали, тогда

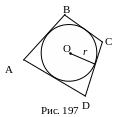4. Рис. 197.

ABCD – четырехугольник,

ω(O,r) – вписанная окружность, тогда

, где р – полупериметр АBCD,

r – радиус вписанной окружности.

VIII.1.2. Четырехугольники и окружность

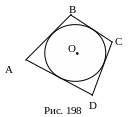
5. Рис. 198.

ABCD – четырехугольник,

ω(O,r) – вписанная окружность, тогда

AB+DC=AD+BC.

Верно и обратное утверждение.

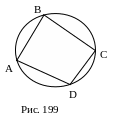6. Рис. 199.

Четырехугольник ABCD,

ω(O,r) – описанная окружность, тогда

Верно и обратное утверждение.

VIII.2. Доказательства утверждений теоретической карты № 8

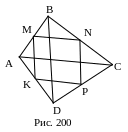
1.

Дано: ABCD – четырехугольник,

K, M, N, P середины его сторон.

Доказать: 1.1MNPK – параллелограмм;

1.2. .

Доказательство.

1.1. ∆АВС: MN – средняя линия ,

∆ADC: КР – средняя линия,

Следовательно, KMNP – параллелограмм.

1.2. ∆MBN ~ ∆АВС с коэффициентом значит, .

Аналогично, . Следовательно, .

. .

2.

Дано: ABCD – четырехугольник,

АС, BD – диагонали, АС=d₁, BD=d₂.

.

Доказать: .

Доказательство.

,

,

S_ABCD=S_AOB+S_BOC+S_COD+S_DAO= sin(AOOB+OBOC+OCOD+OAOD)=

= sin(AO(OB+OD)+OC(OB+OD))= sin(AOBD+OCBD)= = sinBD(AO+OC)= sinBDAC= d₁ d₂sin

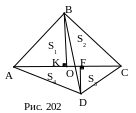
3.

Дано: ABCD – четырехугольник,

АС, BD – диагонали,

S_∆AOB=S₁, S_∆BOC=S₂, S_∆COD=S₃, S_∆DOA=S_4.

Доказать: .

Доказательство.

следовательно, .

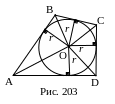4.

Дано: ABCD – четырехугольник,

ω(O,r) – вписанная окружность.

Доказать: ,

где р – полупериметр ABCD,

r – радиус вписанной окружности.

Доказательство.

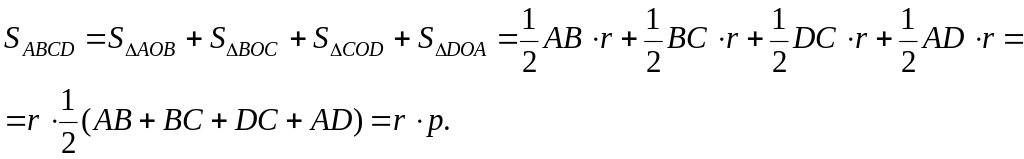
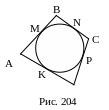5.

Дано: ABCD – четырехугольник,

ω(O,r) – вписанная окружность.

Доказать: AB+DC=AD+BC.

Доказательство.

1) AM=AK, BM=BN, PC=CN, DP=DK.

2) Сложим равенства (1):

AM+BM+PC+DP=AK+BN+CN+DK,

AB+CD=AD+BC.

Докажем обратное утверждение.

Дано: ABCD – четырехугольник,

AB+DC=AD+BC.

Доказать: в четырёхугольник АВСD можно

вписать окружность.

Доказательство.

Метод доказательства – от противного.

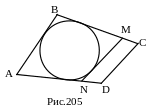
Пусть в четырехугольник АВСD нельзя вписать окружность. Однако окружность, касающаяся трёх сторон четырёхугольника существует (рис. 199).

Проведем касательную к окружности MN, параллельную DC. Тогда по условию

AB+DC=AD+BC=AN+ND+BM+MC. В четырёхугольник ABMN вписана окружность: AB+NM=AN+BM. Подставляя в первое равенство вместо суммы

AN+BM сумму AB+NM, получим AB+DC= AB+NM+ND+MC, следовательно,

DC= NM+ND+MC, что противоречит теореме о длине ломанной.

Таким образом, для того, чтобы в четырёхугольник можно было вписать окружность, необходимо и достаточно, чтобы суммы противоположных сторон четырёхугольника были равны между собой.

5.

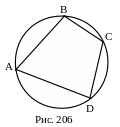
Дано: четырехугольник ABCD,

ω(O,r) – описанная окружность.

Доказать: .

Доказательство.

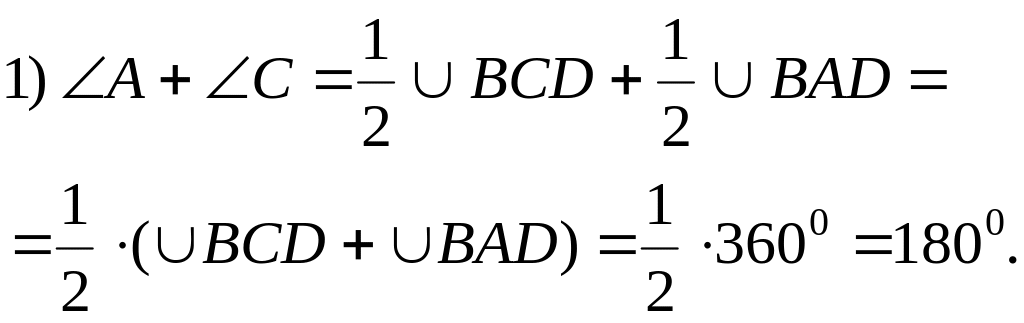
2) Аналогично, 3) Из (1) и (2) следует, что

Докажем обратное утверждение.

Дано: четырехугольник ABCD,

.

Доказать: вокруг четырёхугольника

ABCD можно описать окружность.

Доказательство.

Метод доказательства – от противного.

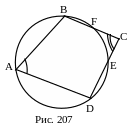
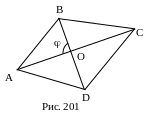
Предположим, что около данного четырёхугольника нельзя описать окружность, однако, существует окружность, проходящая через три его вершины A, B и D. Пусть вершина С лежит вне круга (рис. 201). Тогда , следовательно, Так как то Итак, что противоречит условию. Аналогично можно доказать, что вершина С не лежит внутри круга. Следовательно, вершина С лежит на окружности.

Таким образом, чтобы четырехугольник вписать в окружность, необходимо и достаточно, чтобы суммы его противоположных углов были равны между собой ( причем каждая из них составляет180°).