Вопрос 6.

Общее уравнение плоскости и уравнение первого порядка в пространстве. Примеры.

Вопрос 7.

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДАННУЮ ТОЧКУ

Рассмотрим в пространстве произвольную плоскостьσ. Её положение определяется заданием вектора  , перпендикулярного этой плоскости, и некоторой фиксированной точкиM₀(x₀, y₀, z₀), лежащей в плоскости σ.

В ектор   перпендикулярный плоскости σ, называется нормальным вектором этой плоскости. Пусть вектор   имеет координаты  .

Выведем уравнение плоскости σ, проходящей через данную точку M₀ и имеющей нормальный вектор  . Для этого возьмём на плоскости σ произвольную точку M(x, y, z) и рассмотрим вектор  .

Для любой точки M σ вектор  .Поэтому их скалярное произведение равно нулю  . Это равенство – условие того, что точка Mσ. Оно справедливо для всех точек этой плоскости и нарушается, как только точка M окажется вне плоскости σ.

Если обозначить через   радиус-вектор точки M,   – радиус-вектор точкиM₀, то   и уравнение можно записать в виде

.

Это уравнение называется векторным уравнением плоскости. Запишем его в координатной форме. Так как  , то

.

Итак, мы получили уравнение плоскости, проходящей через данную точку. Таким образом, для того чтобы составить уравнение плоскости, нужно знать координаты нормального вектора и координаты некоторой точки, лежащей на плоскости.

Заметим, что уравнение плоскости является уравнением 1-ой степени относительно текущих координат x, y и z.

Примеры.

Составить уравнение плоскости, проходящей через точку М(1;-2;3) перпендикулярно вектору  .

Используя выведенное уравнение, получим 2(x-1)+0(y+2)+4(z-3)=0 или x+2z-7=0.

Составить уравнение плоскости, проходящей через точки A(1;2;3), B(-1;0;0), C(3;0;1).

Чтобы составить требуемое уравнение, нужно найти вектор перпендикулярный плоскости. Заметим, что таким вектором будет вектор  . Найдем это вектор.  . Тогда

.

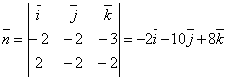Взяв в качестве точки, через которую проходит плоскость точку A, получим уравнение –2(x-1)-10(y-2)+8(z-3)=0 или x+5y-4z+1=0.

Вопрос 8.

Расстояние от точки до точки на плоскости, формула.

Получим формулу для вычисления расстояния между точками и , заданными в прямоугольной декартовой системе координат на плоскости.

Проведем через точки А и В прямые, перпендикулярные координатным осям Ох и Оу. Обозначим проекции точки А на оси Ох и Оу как и соответственно, а проекции точки В как и .

В зависимости от расположения точек А и В возможны следующие варианты.

Если точки А и В совпадают, то расстояние между ними равно нулю.

Если точки А и В лежат на прямой, перпендикулярной оси абсцисс, то точки и совпадают, а расстояние равно расстоянию . В предыдущем пункте мы выяснили, что расстояние между двумя точками на координатной прямой равно модулю разности их координат, поэтому, . Следовательно, .

Аналогично, если точки А и В лежат на прямой, перпендикулярной оси ординат, то расстояние от точки А до точки В находится как .

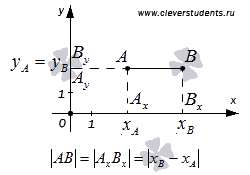
Сейчас будем считать, что точки А и В не совпадают и не лежат на прямой, перпендикулярной координатной оси. Найдем расстояние между ними.

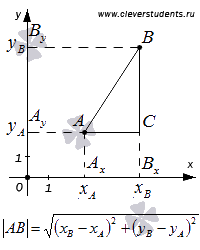
В этом случае треугольник АВС – прямоугольный по построению, причем и . По теореме Пифагора мы можем записать равенство , откуда .

Обобщим все полученные результаты: расстояние от точки до точки на плоскости находится через координаты точек по формуле .

Полученную формулу для нахождения расстояния между точками, можно использовать когда точки А и В совпадают или лежат на прямой, перпендикулярной одной из координатных осей. Действительно, если А и В совпадают, то . Если точки А и В лежат на прямой, перпендикулярной оси Ох, то . Если А и В лежат на прямой, перпендикулярной оси Оу, то .