12. Интегрирование иррациональных функций

Основным методом решения интегралов от иррациональных выражений является метод замены переменной. Цель замены – преобразовать данное иррациональное выражение к рациональной дроби.

 сводится к 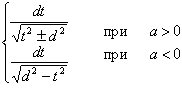 , предварительно необходимо выделить полный квадрат под знаком корня, сделать замену и проинтегрировать по таблице интегралов

2.

.

Сделать в числителе производную подкоренного выражения. Разбить на два интеграла, один из которых степенной, а другой вида

3.         

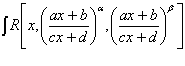
подстановка  ,

 – наименьший общий знаменатель дробей   и  .

4. ,    

,    

,    

5.  – дифференциальный бином интегрируется в трех случаях:

1)   – целое,   – интегрируется непосредственно,

           – подстановка  , где   – общий знаменатель дробей

               и  ;

2)   – целое ( ,  ,  ) подстановка  , где   – знаменатель

         дроби  ;

3)   – целое ( ,  ,) подстановка  .

13. Определенный интеграл. Формула Ньютона-Лейбница

Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю:

где

Формула Ньютона-Лейбница

Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на[a, b], то

14. Замена переменной в определенном интеграле

При замене переменной в определенном интеграле не нужно возвращаться к исходной переменной интегрирования

15. Интегрирование по частям в определенном интеграле

Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

для определённого:

для определённого интеграла

В целом аналогично случаю неопределённого интеграла:

16. Вычисление площадей в прямоугольных координатах

Пусть на плоскости  задана область, ограниченная снизу кривой   , заданной в декартовых координатах, сверху – кривой   , слева – прямой    (ее может и не быть, если   ), справа – прямой   .Исходя из геометрического смысла определенного интеграла, площадь этой области можно вычислить по формуле    . Здесь не нужно заботиться, какая из функций и где положительная, а какая отрицательная. Если, например,  , то формула сама прибавит нужную площадь. Более сложные области всегда можно разбить так, чтобы выполнялись указанные условия.

17. Несобственные интегралы. Интеграл с бесконечными пределами интегрирования

При определении интеграла

     (1)

предполагалось, что: 1) отрезок интегрирования [a, b] конечен и 2) подынтегральная функция f(x) на этом отрезке непрерывна. Такой определенный интеграл называется интегралом в "собственном смысле", или собственным интегралом. В том же случае, когда отрезок интегрирования бесконечен или конечен, но подынтегральная функция на этом отрезке терпит разрыв, то (1) называется интегралом в "несобственном смысле" или несобственным интегралом.

Пусть функция f(x) непрерывна при a ≤ x < +∞. Тогда по определению полагают

     (2)

Если предел (2) существует, то несобственный интеграл с бесконечным пределом интегрирования, стоящий в левой части равенства (2), называется сходящимся и его значение определяется формулой (2); в противном случае равенство (2) теряет смысл, несобственный интеграл, стоящий слева, называется расходящимся и ему не приписывается никакого числового значения.

     Интеграл   определяется аналогично:

     (3)

а интеграл

     (4)

при этом

     (5)

где a - любое число.