§ 6. Теорема сложения вероятностей совместных событий.
Определение 1. Два события называют совместными, если появление одного из них не исключает появление другого в одном и том же испытании.
Пример 1. А – появление 4-х очков при бросании игральной кости; В появление четного числа очков. А и В – совместные события.
Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий А и В равна:
(1)
Доказать самостоятельно.
З
А
В
.
Замечание 2.
Если событие А и В несовместны, то
и - эту формулу уже рассмотрели.
Пример
2. Вероятности
попадания в цель при стрельбе первого
и второго орудий:
.
Найти вероятность попадания при одном
залпе из обоих орудий хотя бы одним из
них.
Решение:
.
Можно решить иначе,
т.к. события А и В независимые, то искомая
вероятность:
.
§ 7. Формула полной вероятности.
Пусть событие А
может наступить при условии появления
одного из несовместных событий:
,
которые образуют полную группу. Известны
вероятности:
,
условные вероятности:
.
Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий образующих полную группу находится по формуле:
- это формула полной
вероятности.
Пример. Имеются два набора деталей. Вероятность того, что деталь первого набора стандартная 0,8; а второго: 0,9. Найти вероятность того, что взятая наудачу деталь из взятого наудачу набора стандартная.
Решение. Событие А – извлеченная деталь стандартная.
1) Деталь можно извлечь либо из 1-го набора (событие В1), либо из второго (событие В2) .
2)
Вероятность того, что деталь извлечена
из 1-го набора:
и того, что она извлечена из 2-го:
.
3)
Условная вероятность того, что из 1-го
набора извлечена стандартная деталь:
;
а условная вероятность того, что из 2-го
набора вынута стандартная деталь
.
4)
По формуле полной вероятности:
§ 8. Формула Бейеса.
Пусть событие А может поступить при условии появления одного из несовместных событий , образующих полную группу. Т к. неизвестно, какое из этих событий наступит, их называют гипотезами.
По формуле полной вероятности получим:
.
(*)
Пусть проведено
испытание и событие А произошло, как
при этом изменились вероятности гипотез;
т.е. необходимо найти условные вероятности:
.
Вывести следующую формулу самостоятельно:
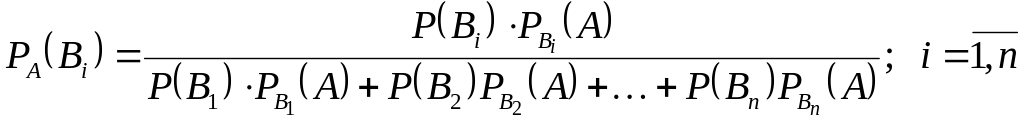
Эти формулы называются формулами Бейеса (английский математик, вывел их в 1764г.). В предыдущем примере:
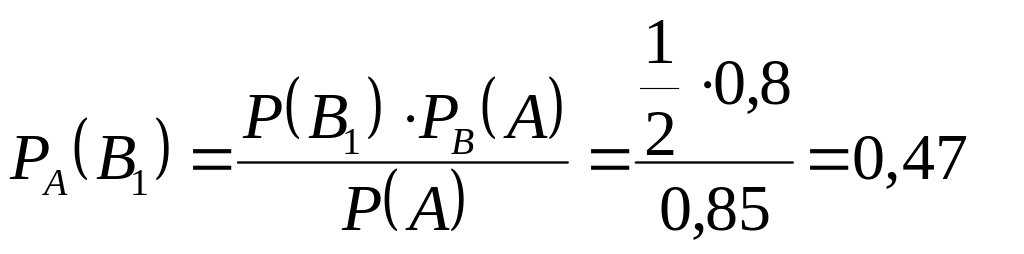
Тема: Повторение испытаний. Формула Бернулли.
Локальная и интегральная теоремы Лапласа.
§ 1. Формула Бернулли.
Если производится несколько испытаний причем вероятность события А в каждом испытании не зависит от исхода других испытаний, то такие испытания называют независимыми относительно А.
В разных независимых испытаниях событие А, может иметь либо различные вероятности, либо одну и ту же вероятность.
Будем рассматривать только такие независимые испытания, в которых событие А имеет одну и ту же вероятность.
Под сложным событием будем понимать совмещение нескольких отдельных событий, которые называют простыми.
Пусть производится
n
независимых испытаний, в каждом из
которых событие А
может либо появится, либо не появится.
Вероятность события А
в каждом испытании равна р.
Тогда вероятность ненаступления события
А
в каждом испытаний тоже постоянна и
равна:
.
Необходимо вычислить
вероятность того, что при n
испытаниях событие А
произойдет ровно k
раз и не
произойдет n
– k
раз. Обозначим эту вероятность
.
Эта вероятность находится по формуле
Бернулли:
,
(вывести самостоятельно).
или
(*)
Пример.
Вероятность того, что расход электроэнергии
в течение суток не превысит установленной
нормы равна
.
Найти вероятность того, что в течение
ближайших 6 суток расход электроэнергии
в течение 4-х суток не превысит нормы.
Решение.
Вероятность нормального расхода в
каждые сутки тоже постоянна:
.
Искомая вероятность по формуле Бернулли:
.
Замечание. При больших значениях n пользоваться формулой (*) трудно. Вычисления будут трудоемкими. Поэтому существуют другие формулы.