15 17Дифференциальные уравнения 1. Основные понятия

     Определение. Уравнение вида      F(x,y,y',y'',…,y⁽ⁿ⁾) = 0,                                                    (*)      связывающее аргумент х, функцию у(х) и ее производные, называется дифференциальным уравнением n-го порядка.      Определение. Общим решением дифференциального уравнения n-го порядка называется функция у = φ(х, С₁,С₂,…,С_n), которая зависит от аргумента х и n независимых произвольных постоянных С₁, С₂, …, С_n, обращающая вместе со своими производными у', у'',…, у⁽ⁿ⁾ уравнение (*) в тождество.      Определение. Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С₁, С₂, …, С_n определенные числовые значения.

2. Линейные дифференциальные уравнения первого порядка

     Определение. Уравнение вида y'+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.      Пример. Найти общее решение уравнения y'+3y=e^2x и частное решение,удовлетворяющее начальным условиямх=0, у=1.      Решение. Данное уравнение является линейным.      Здесь ρ(x)=3 и f(x)=e^2x.      Решение ищем в виде y=U∙υ, где U и υ – некоторые функции от х. Находим y'= U'υ+ Uυ' и подставляем в уравнение значение y и y', получаем: U'υ+Uυ'+3Uυ=e^2 x или U'υ+U(υ'+3υ)= e^2x.      Найдем одно значение υ, при котором выражение в скобках, обращается в нуль: υ'+3υ=0. Получим уравнение с разделяющимися переменными. Решая его получаем:      ln υ =–3x,υ=e^–3x.      Подставляем найденное значение υ в исходное дифференциальное уравнение, получаем уравнение с разделяющимися переменными:        .      Итак, общее решение данного уравнения имеет вид:        .      Найдем частное решение. Для этого подставим  начальные условия в выражение для общего решения и найдемС.       .      Частное решение имеет вид:  .

16Уравнения с разделяющимися переменными

Дифференциальное уравнение   называется уравнением с разделяющимися (отделяющимися) переменными, если его правая часть представима в виде  . Тогда, в случае  , общим решением уравнения является  .

18Дифференциальные уравнения, допускающие понижение порядка.

В этой статье рассмотрим дифференциальные уравнения порядка выше второго, в которых есть возможность понижения порядка с помощью замены. Среди таких уравнений наиболее часто встречаются ОДУ  , которые не содержат искомой функции и производных до k – 1 порядка, и дифференциальные уравнения вида  , которые не содержат независимого переменного. Порядок дифференциального уравнения   может быть снижен до n – kзаменой переменных  . При такой замене получим  . После подстановки этих результатов в исходное уравнение получим дифференциальное уравнение порядка n – k с неизвестной функциейp(x). После нахождения p(x), функция y(x) может быть найдена из равенства  интегрированием k раз подряд. Рассмотрим примеры. Пример. Найдите общее решение дифференциального уравнения  . Решение. Заменой   порядок дифференциального уравнения может быть снижен с четвертого до второго. Действительно,  , и исходное ОДУ преобразуется к линейному однородному дифференциальному уравнению второго порядка с постоянными коэффициентами  . Его характеристическое уравнение имеет вид  . Корнями характеристического уравнения являются   и  , следовательно,  . Дважды проинтегрировав этот результат, получим искомое общее решение:   Ответ: 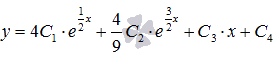 , где С₁, С₂, С₃ и С₄ – произвольные постоянные. Пример. Найдите общее решение дифференциального уравнения  . Решение. Пусть  , тогда   и исходное уравнение сводится к уравнению с разделяющимися переменными  . Разделяем переменные и интегрируем: 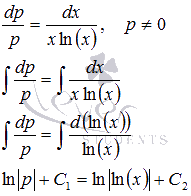  Потенцируя полученное равенство и учитывая, что p(x) = 0 также является решением, получаем  , где C – произвольная постоянная. Так как  , то  , следовательно,  . Воспользуемся методом интегрирования по частям: 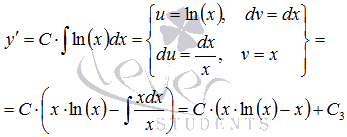  Интегрируем еще раз, чтобы получить искомое общее решение: 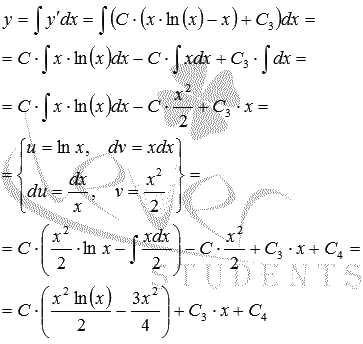  Ответ:  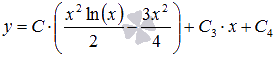, где С, С₃ и С₄ – произвольные постоянные. Переходим к дифференциальным уравнениям вида  , которые не содержат независимого переменного. Порядок таких дифференциальных уравнений можно снизить на единицу заменой 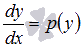 . Тогда поправилу дифференцирования сложной функции имеем 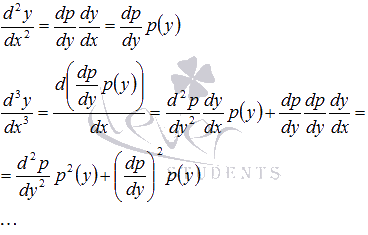  Подставляя эти результаты в исходное уравнение, приходим к дифференциальному уравнению, порядок которого на единицу ниже. Разберем на примере. Пример. Найдите частное решение дифференциального уравнения  , удовлетворяющее начальным условиям 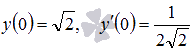 . Решение. Исходное дифференциальное уравнение не содержит независимой переменной x, поэтому его порядок может быть снижен на единицу заменой  . Тогда 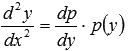  и после подстановки получаем дифференциальное уравнение с разделяющимися переменными 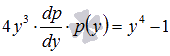 . Интегрируем его: 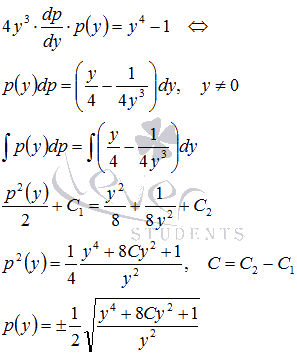  Так как  , то 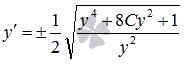 . На этом этапе есть возможность определить константу C, обратившись к начальным условиям  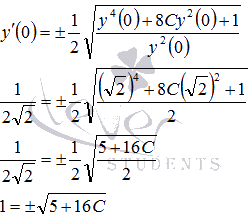:   Из последнего равенства можно сделать вывод, что 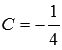 ,а 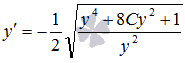  не удовлетворяет условиям задачи. 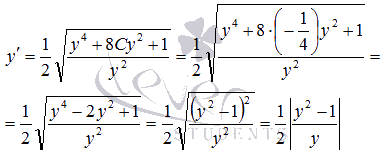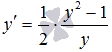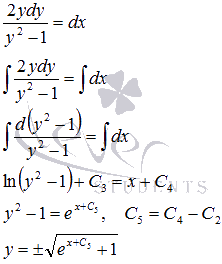Поэтому   При   имеем  , откуда   Область значений функции   есть (- ∞, - 1], а этот интервал не удовлетворяет условию  , поэтому   не рассматриваем. Воспользуемся начальным условием  :  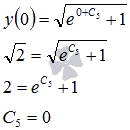 Следовательно,   - искомое частное решение. 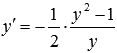При   имеем  , откуда  . Областью значений функции   является интервал [1, +∞), а этот интервал не удовлетворяет условию  , поэтому   не рассматриваем. Для функции   начальное условие   не удовлетворяется ни для каких С₆, так как 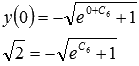Ответ:  .Примеры физических задач, приводящих к уравнениям с разделяющимися переменными