9. Интегралы вида вычисляются при помощи подстановок Эйлера.

1. a>0. Сделаем замену x на t следующим образом:

возведем в квадрат: отсюда - рациональная функция от t.

Окончательно.

2. с>0. Применим подстановку 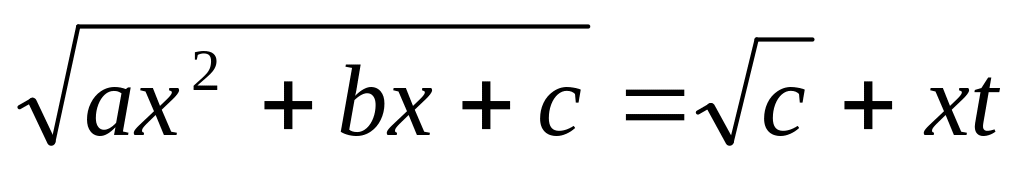. Возводя в квадрат, получим , откуда 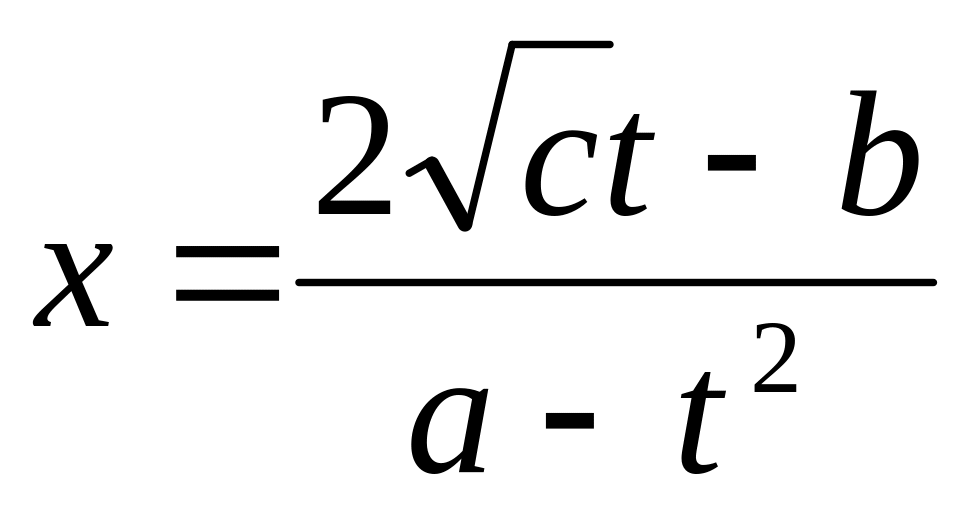- рациональная функция. В итоге получим

.

3.Корни трехчлена вещественные. Т.е.

Сделаем подстановку , где t>0 при или t<0 при . Возводя в квадрат, получим , откуда . В итоге

_.

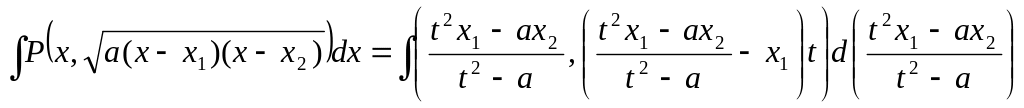10.Интегралы вида :

Подстановка вида u = tg(x/2) сводит интеграл к интегралу от рациональной дроби.

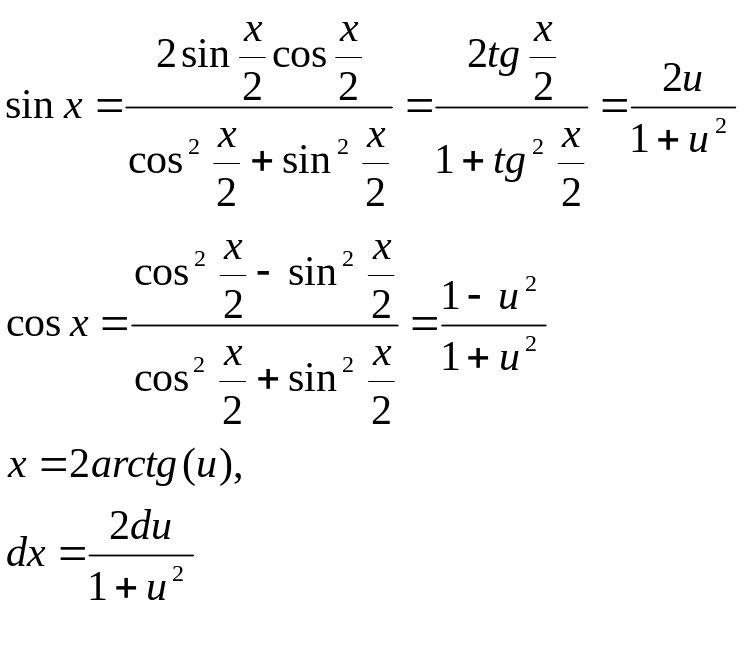
Поэтому Т.о. получился интеграл от рациональной функции.

Но вместе с тем используются другие вида u=sin x, u=cos x, u=tg x.

1. :

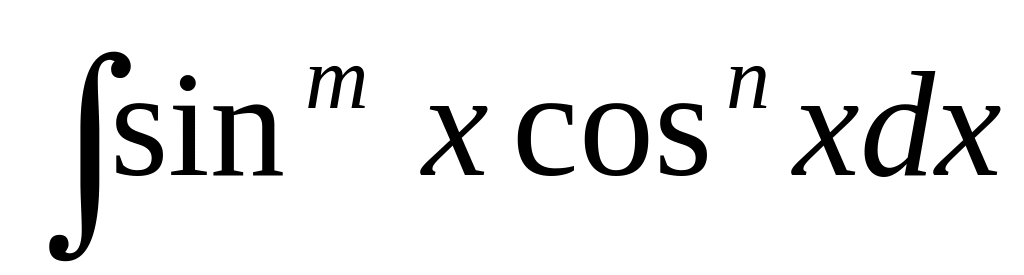Пусть m и n – рациональные числа. Тогда интеграл с помощью подстановок u=sin x или u=cos x сводится к интегралу от дифференциального бинома (т.е. , ( )).Напр. 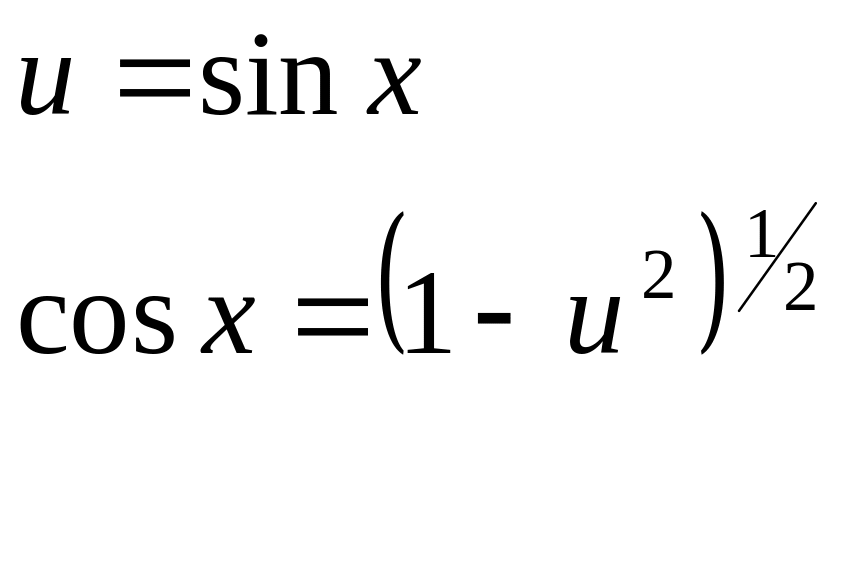, , , поэтому

.

Т.о., интеграл выражается или нет через элементарные функции в зависимости от того, обладает этим свойством диф. бином (подстановки Чебышева).

Если m и n целые (не обязательно положительные) применяют подстановки u=sin x, u=cos x, u=tg x.

Например, если m=2k+1 (или n=2k+1) : пусть u=cos x

. Т.о. интеграл сведен к интегралу от рациональной дроби.

Если m и n положительные и четные применяют формулы понижения степени: , .

2. :

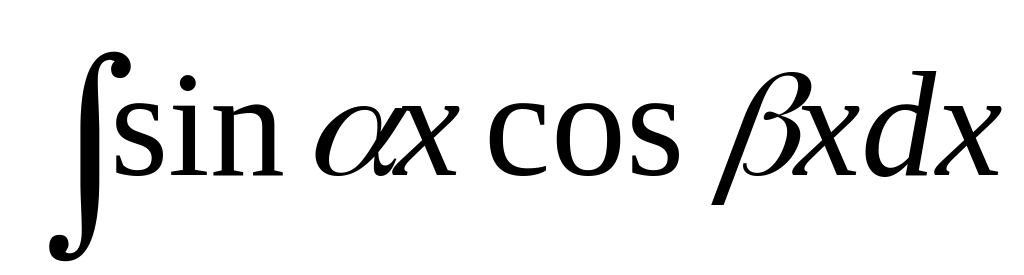Интегралы непосредственно вычисляются после преобразования подынтегральных функций по формулам:

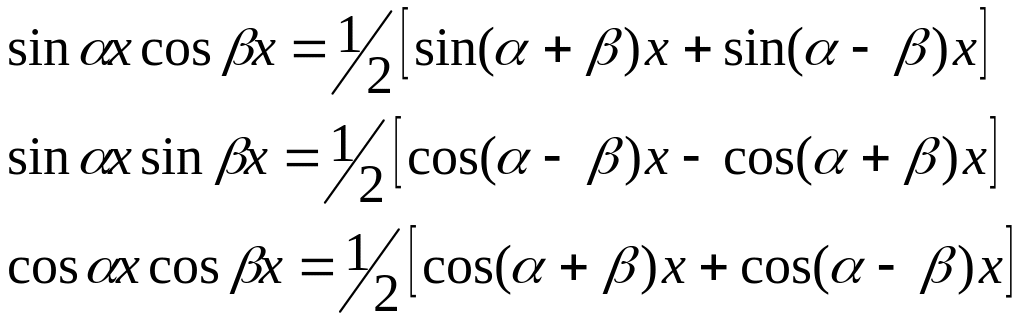
11.Рассмотрим функцию f(X), определенную в каждой точке сегмента [a,b].

Введем понятие разбиения сегмента, измельчение этого разбиения и объединение двух разбиений.

ОПР. Будем говорить, что задано разбиение сегмента [a,b], если заданы точки x₀,x₁,x₂…x_n такие, что а=x₀<x₁<x₂…<x_n=b. Разбиение сегмента будем обозначать {x_k}.

ОПР. Разбиение {x_k’} сегмента [a,d] называется измельчением разбиения {x_k} того же сегмента, если каждая точка xp принадлежит {x_k}, совпадает с одной из точек x_q’из {x_k’}.

ОПР. Разбиение {x_k} сегмента [a,b] называется объединением {x_k’},{x_k”} того же сегмента, если все точки разбиений {x_k’}, {x_k”} являются точками разбиения {x_k} и других точек {x_k}не содержат.

Рассмотрим на сегменте [a,b] функцию f(x), принимающую в каждой точке сегмента конечные значения. По данному разбиению {x_k} построим число, так называемую интегральную сумму.

n

σ =∑f(ξ_k)(x_k-x_k-1),

k=1

где ξ_k - некоторая точка [x_k-1,x_k].

Подчеркнем, что σ (x_k,ξ_k) зависит от разбиения {x_k} и от выбора точек ξ_k на [a,b]. Обозначим ∆x_k=x_k-x_k-1, то

n

σ =∑f(ξ_k) ∆x_k,

k=1

ξ_k [x_k-1,x_k]

[x_k-1,x_k] - называется частичным сегментом, а ξ_k - промежуточной точкой.

Число d = max ∆x_k называется диаметром разбиения {x_k} .

Число I называется пределом интегральных сумм σ(x_k,ξ_k) при стремлении d разбиения {x_k} к нулю, если для любого ε > 0, существует число δ > 0, что при d < δ при любом выборе промежуточных точек ξ_k следует

׀I - σ׀ < ε, I = lim σ(x_k,ξ_k), d→0

ОПР. Функция f(x) называется интегрируемой по Риману на сегменте [a,b],если для этой функции на указанном сегменте существует предел I ее интегральных сумм σ при стремлении диаметра d разбиения {x_k} к нулю.

Число I называется определенным интегралом функции f(x) в

b

пределах от a до b и обозначается: ∫f(x)dx

a

Т.о. b

∫f(x)dx= lim σ(x_k,ξ_k) ,d→0

a

a - нижний предел, b - верхний предел.

Необходимое условие интегрируемости:

Если функция f(x) не является ограниченной на сегменте [a,b], то она не интегрируема на этом сегменте.

ДОК. От противного.

Пусть f(x) не ограничена на, а это по определению неограниченной функции значит ,что для любого n, существует ε, что ׀f(x)׀ > ε, тогда

существует подпоследовательность значений функции {x_n},что

f(x)→∞

Возьмем произвольное разбиение p, т.к. количество отрезков конечно, а количество точек бесконечно, значит существует хотя бы один отрезок ∆_i, которому принадлежит подпоследовательность количества точек{x_nk}, x_nk∆_i. Точки ξ_i зададим точками x_nk, то получим в сумме ∑f(x_nk)∆x_i, слагаемое f(x_nk)∆x_i стремится к ∞, σ_n(p) = ∞ при заданном р. Это означает, что конечного придела интегральных сумм нет, т.е. f(x) не интегрируема, а это говорит о том, что только ограниченная функция интегрируема.

_{12. Пусть ограниченная на сегменте [a,b] функция f(x) и {xk} произвольное разбиение этого сегмента. Т.к. f(x) ограниченная на сегменте [a,b], то она ограничена на любом частичном сегменте [xk-1,xk], а поэтому у функции существует точная верхняя Mi и нижняя mi грани на частичном сегменте [xk-1,xk]. Итак, пусть Mk=sup f(x), mk=inf f(x), где xk-1< x < xk.}

Введем фундаментальное понятие верхних и нижних сумм.

ОПР.Суммы

n

S = M₁∆x₁+M₂∆x₂+…+M_n∆x_n = ∑M_k∆x_k

k=1

n

s = m₁∆x₁+m₂∆x₂+…+m_n∆x_n = ∑m_k∆x_k

k=1

Будем называть соответственно верхней и нижней суммами функции f(x) для данного разбиения {x_k} сегмента [a,b] .

Свойства:

ЛЕММА1.

Пусть σ(x_k,ξ_k) интегральная сумма отвечающая данному разбиению {x_k}. Тогда при любом выборе промежуточных точек ξ_k всегда справедливо неравенство s  σ  S.

ДОК.

По определению чисел m_k, M_k заключаем, что m_k  f(ξ_k)  M_k для любой ξ_k[x_k-1,x_k]. Умножая написанное неравенство на ∆x_k и суммируя по всем к от 1 до n, получим

n n n

∑m_k∆x_k  ∑f(ξ_k)∆x_k  ∑M_k∆x_k

k=1 k=1 k=1

n n n

∑m_k∆x_k=s, ∑f(ξ_k)∆x_k=σ, ∑M_k∆x_k=S

k=1 k=1 k=1

ЛЕММА 2.

Пусть произвольное фиксированное разбиение {x_k} сегмента [a,b], ε - произвольное положительное число. Тогда можно выбрать промежуточные точки ξ_k так, чтобы интегральная сумма σ(x_k,ξ_k) и верхняя сумма S удовлетворяли неравенству 0  S-σ(x_k,ξ_k). Промежуточные точки ξ_k можно выбрать и таким образом, чтобы для интегральной суммы σ(x_k,ξ_k) и нижней s суммы выполнялись неравенства

0  σ(x_k,ξ_k)–s < ε.

ДОК.

Пусть {x_k} фиксированное разбиение сегмента [a,b] и ε >0.

Докажем утверждение: поскольку M_k=sup f(x), где x_k-1< x < x_k, то для выбранного нами ε >0 найдется точка ξ_k такая, что 0  M_k-f(ξ_k) < ε /(b-a), Умножив эти неравенства на ∆x_k и просуммировав по всем к от 1 до n ,получим

n n n

0  ∑M_k∆x_k - ∑f(ξ_k)∆x_k < ∑∆x_kε/(b-a)  0  S-σ(x_k,ξ_k) < ε

k=1 k=1 k=1

Анологично в силу того, что m_k=inf f(x), x_k-1  x  x_k, существует такая точка n_k[x_k-1,x_k], что

0  f(n_k)-m_k < ε/(b-a) ׀* ∆x_k, получим 0  σ(x_k,ξ_k)-s < ε.

ЛЕММА 3.

При измельчении данного разбиения нижняя сумма может только увеличиться, а верхняя только уменьшиться.

ДОК.

Пусть {x_k} данное разбиение, а {x_k’} получается из него добавлением одной точки x’. Предположим, что x’ лежит внутри [x_k-1,x_k].

Тогда в выражении для S слагаемое M_k∆x_k замениться на M’_k(x’-x_k-1) + M”_k(x_k-x’),

M’_k = sup f(x), x_k-1  x  x’

M”_k = sup f(x), x’  x  x_k

Точная верхняя грань функции на части сегмента не превосходит точной верхней грани функции на всем сегменте. Поэтому M’_k  M_k, M”_k  M_k

M’_k(x’-x_k-1) + M”_k(x_k-x’)  M_k[(x’-x_k-1)+ (x_k-x’)] = M_k∆x_k

Sup{f(x)}  sup{f(x)}

x{x_k’} x{x_k}

СЛЕД.

К разбиению P_n добавим P_m, получим разбиение P_n P_m =P_n+m. P_n, P_m  s(P_n)  S(P_m)

ОПР. Верхним интегралом Дарбу от функции f(x) называется число I*, равное точной нижней грани множества верхних сумм {S} данной функции для всевозможных разбиений сегмента [a,b] I*=inf S(p)

ОПР. Нижним интегралом Дарбу называется число I**, равное точной верхней грани множества нижних сумм {s} данной функции f(x) для всевозможных разбиений сегмента [a,b] I**=inf s(p).

Критерий Дарбу интегрируемости по Риману.

Пусть функция f(x) определена и ограничена на сегменте [a,b]. f(x) будет интегрируема тогда и только тогда, когда lim(S-s)=0, или, что то же самое, ε>0,существует δ, p таких, что λ(p)<δ или S-s<ε

n n

∑(Mi-mi)∆xi<ε или ∑(f,∆i)∆xi<ε.

k=1 k=1

ДОК.

→Пусть выполняется, что f(x) интегрируема на [a,b], докажем lim(S-s)=0.

Существует такое число I со свойством, что ε>0, существует δ, p таких, что λ(p)<δ, {ξ}

Выполняется

n

| ∑f(ξi)∆xi – I|<ε.

k=1

для каждого промежутка ∆I :mi f(ξi) Mi ,тогда s(p) σ(p) S(p).

Зафиксируем ε=ε/2 ,т.к. мы можем взять любое ε .Получаем

׀σ – I ׀<ε : I-ε/2 < σ < I+ε/2 =>

n

∑f(ξi)∆xi < I+ε/2.

k=1

УТВ.

а1+а2+а3+…+аn<k, где а1 принадлежит множеству х1, а2 - х2, выбираем sup из чисел sup(a1+a2+a3+…+an)=sup(a1)+sup(a2)+sup(a3)+…+sup(an).

Если перейти к неравенству, то получим

n

∑Mi∆xi  I+ε/2, =>I-ε/2  S  I+ε/2, => I-ε/2  s  I+ε/2,

k=1

т.к. интегральные суммы зажаты между двумя числами, то и суммы Дарбу зажаты между этими числами, т.е. при вычитании неравенств получаем ε  S-s  ε => lim(S-s)=0.

←Пусть lim(S-s)=0 докажем, что f(x) интегрируема.

Если выполняется s  I**  I*  S (два числа зажаты между двумя последовательностями), это значит, что I* = I** = I, показать, что

׀σ –I׀<ε при любом р с условием λ(p)<δ.

I**=sup s(p), I*=inf S(p)

n

I-ε  ∑mi∆xi  I+ε,

k=1

n

I  ∑Mi∆xi  I+ε , => s < σ < S => s  I  S. Т.к. дан lim(S-s)=0 =>

k=1

limσ=0, S-s<ε, если λ(p)<δ => ׀σ –I׀<ε

_{Т.к. границы S и s можно сделать сколь угодно малыми, то разность σ-I тоже может быть сколь угодно малой.}