10. Основные теоремы о пределах.

1.  Предел константы равен самой этой константе:

 с = с.

2.  Постоянный множитель можно выносить за знак предела:

 [ k •  f (х)] = k •    f (х).

3.  Предел суммы (разности) функций равен сумме (разности) пределов этих функций:

 [ f (х) ± g (х)] =    f (х) ±   g (x).

4.  Предел произведения функций равен произведению пределов этих функций:

 [ f (х) • g (х)] =    f (х) •   g (x).

5.  Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю:

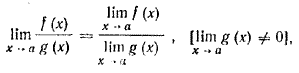
11. Первый и второй замечательные пределы. (это что за хрень?))))

Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известныхматематических тождеств со взятием предела. Особенно известны:

• Первый замечательный предел:

• Второй замечательный предел:

Мультики вот тут

http://webmath.exponenta.ru/s/kiselev1/node18.htm

http://www.mathprofi.ru/zamechatelnye_predely.html

12. Раскрытие неопределённостей, правило Лопиталя.

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.

Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.

Для раскрытия неопределённостей видов  ,  ,   пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

Для раскрытия неопределённостей типа   используется следующий алгоритм:

1. Выявление старшей степени переменной;

2. Деление на эту переменную как числителя, так и знаменателя.

Для раскрытия неопределённостей типа   существует следующий алгоритм:

1. Разложение на множители числителя и знаменателя;

2. Сокращение дроби.

Для раскрытия неопределённостей типа   иногда удобно применить следующее преобразование:

Пусть   и 

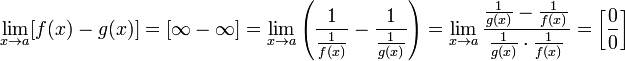
Пример

«Замечательный предел»   — пример неопределённости вида 0 / 0. По правилу Лопиталя

13. Непрерывность функции в точке и на интервале.

Определение 1. Пусть функция   определена в окрестности точки  , тогда функция непрерывна в  , если  .

****************************************

Определение 2. Функция   непрерывна, если .

***************************************

Определение 3. Функция   непрерывна в точке  , если  .Приращение аргумента  . Приращение функции  .

***********************************

Определение 4. Функция   непрерывна в точке  , если  . Если функция не является непрерывной в точке  , то эта точка – точка разрыва. Если функция непрерывна на отрезке (a, b), то функция неразрывна на отрезке (a, b).

 

*****************************************

Определение 5. Функция   непрерывна в точке   справа, если  .

****************************************

Определение 6. Функция   непрерывна в точке   слева, если  .

Функция непрерывна на отрезке  , если она непрерывна в каждой внутренней точке этого отрезка и односторонне непрерывна на его концах.