23.2 Определение положения равновесия

Рассмотрим механическую систему с идеальными, стационарными и голономными связями, положение которой определяется независимыми обобщенными координатами 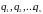. Для изучения колебаний около положения равновесия, необходимо, прежде всего, найти эти положения.

Хорошо известно ещё из физики, что в положении равновесия все обобщенные силы равны нулю:

(*)

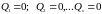Тогда для консервативной системы

В силу консервативности и стационарности системы 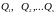зависят только от . Тогда равенства (*) можно рассматривать как уравнения относительно .

Решая эти уравнения, найдем те положения, в которых система может находиться в равновесии. Если обобщенные силы зависят не только от , но и от обобщенных скоростей , то при решении уравнений (*) все следует приравнять нулю.

Во многих случаях положения равновесия можно определить из элементарных соображений или с помощью обычных уравнений статики. Рассмотрим этот вопрос на примере.

П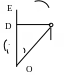 ример. Определим возможные положения равновесия маятника со спиральной пружиной с угловой жесткостью С, изображённой на Рис. 23.5. Здесь вес маятника равен Р, расстояние от оси подвеса О до центра тяжести равно . В верхнем вертикальном положении маятника спиральная пружина находится в недеформированном состоянии. Массой пружины и трением в подшипнике в нашей модели пренебрегаем.

З

С

аметим, что система имеет одну степень свободы. В качестве обобщенной координаты возьмём угол . Потенциальная энергия системы П складывается из потенциальной энергии силы тяжести и

Рис. 23.5

потенциальной энергии спиральной пружины.

За нулевой уровень потенциальной энергии примем верхнее вертикальное положение маятника. Тогда, в текущем положении маятника потенциальная энергия примет вид

Из физики известно, что для закручивания спиральной пружины на малый угол требуется приложить внешнюю пару сил с моментом , где с – коэффициент угловой жесткости. Тогда потенциальная энергия сил упругости согласно 9.3, будет равна .

При этом полная энергия маятника будет равна

Составим уравнение равновесия: . Это же уравнение можно вывести из условия равновесия стержня.

Возникает вопрос: Какими должны быть параметры системы, чтобы маятник мог находиться в заданном положении равновесия?

Ответим на этот вопрос. Допустим, состояние равновесия определяется углом . Тогда и (*)

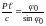В частности, если потребуется, чтобы пружина удерживала маятник в горизонтальном положении , будем иметь: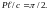 При таком соотношении параметров маятник может находится в равновесии, занимая горизонтальное положение.

Решим обратную задачу. Пусть заданы параметры . Определим возможные положения равновесия маятника. Запишем(*) в виде

, где . (**)

Здесь один корень уравнения очевиден: ! Этому корню отвечает верхнее вертикальное положение равновесия маятника. Для определения других возможных положений равновесия нужно найти остальные корни трансцендентного уравнения (**). Их можно определить различными методами, например, табличным или графическим. Поясним графический способ решения. Составим два уравнения: ; .

Рис.23.6

Очевидно, что второй корень уравнения 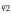определяется абсциссой точки пересечения обоих графиков. Причем каждому положительному отвечает равный по модулю, но отрицательный корень . Физически это означает, что положение равновесия маятника могут быть как слева, так и справа от вертикали. Кроме того, видно, что при ( ) прямая не пересекает синусоиду . В этом случае уравнение (**) имеет один тривиальный корень .