3.2 Текущий и окончательный контроль вычислений в методе Гаусса

Для контроля вычислений параллельно системой решается система где S – вектор.

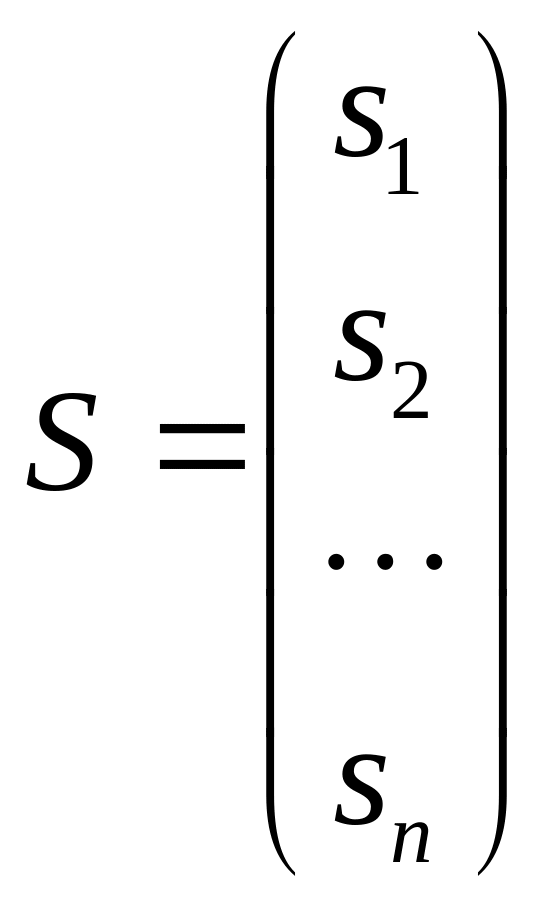
Если над числами выполнять те же действия, что и над числами , то на любом этапе схемы единственного деления и схемы Жордана сумма коэффициентов строки и свободного члена должна давать числа . Это и есть текущий или построчный контроль вычислений. Если эти числа отличаются существенно, а не на одну - две единицы последнего разряда, то в строке допущена ошибка и коэффициенты следует пересчитать.

Эта же система служит и для окончательного контроля вычислений.

Если есть решения системы , то решением системы будет вектор такой, что

Доказательство: подставим в левую часть уравнения , будем иметь

Таким образом, окончательный контроль заключается в том, что решения систем и должны отличатся на единицу.

3.3 Уточнение корней

Решение, получаемое по методу Гаусса, является приближенным, то есть

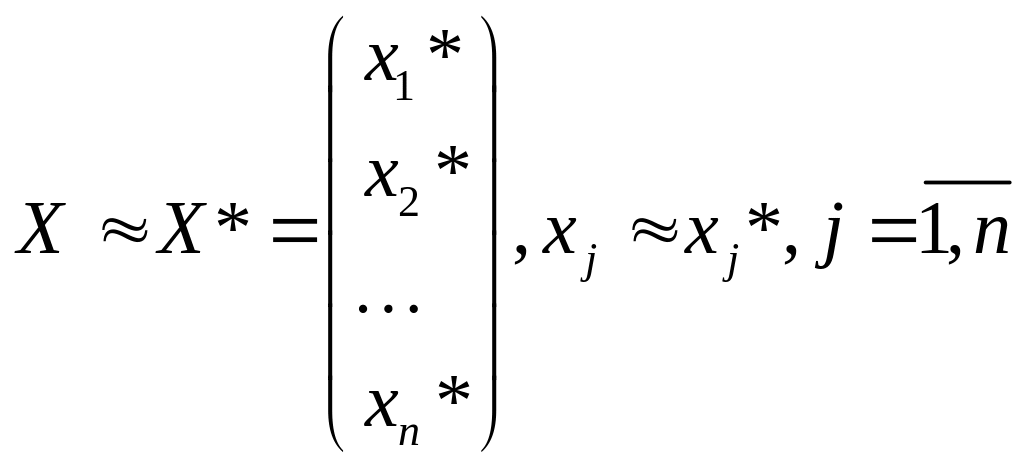
Решение можно уточнить.

Если подставить в уравнение (1’), получим приближенное равенство.

Разность называют невязкой.

Так как , то называется поправкой

Так как , то получаем вектор поправок

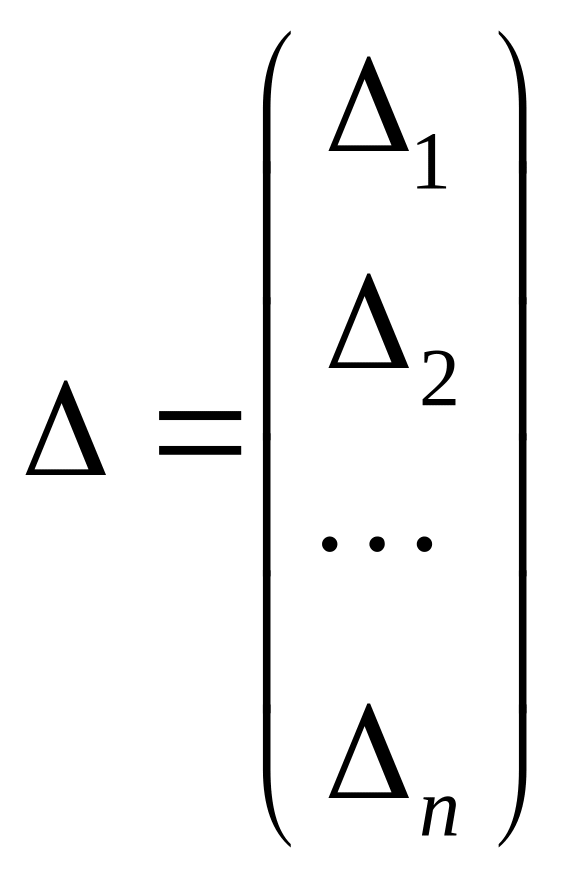
Подставим вектор X в систему ( 2 )

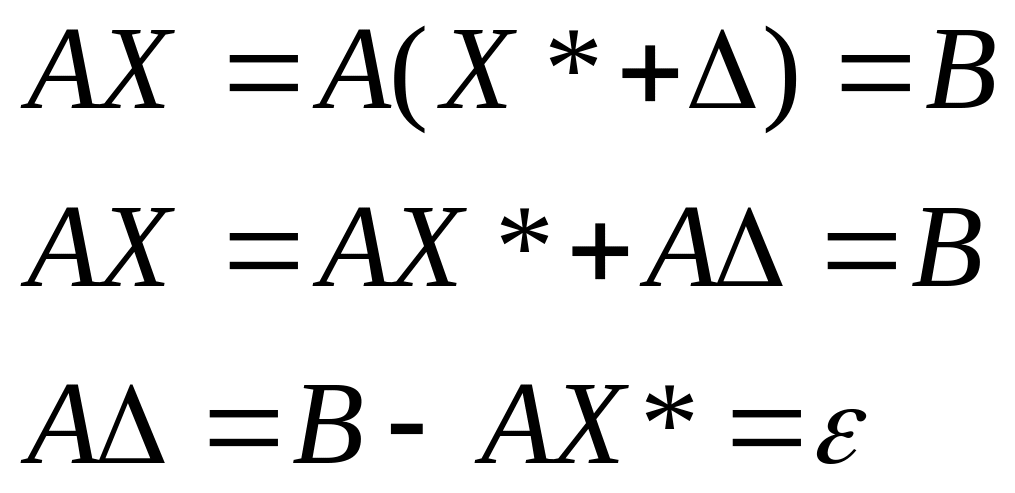
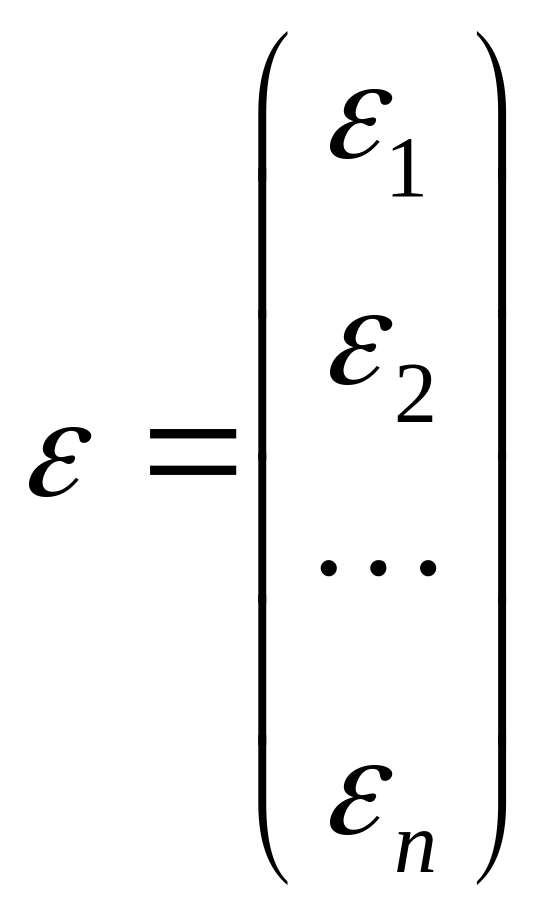вектор невязок

Решение новой системы с той же матрицей коэффициентов, но с другой правой частью дает вектор поправок.

и можно получить уточненное решение:

3.4 Метод квадратных корней.

Матрица называется транспонированной по отношению к матрице А, если ее столбцы совпадают с соответствующими строками матрицы А, а элементы с одинаковыми индексами – элементы главной диагонали.

Матрица А называется верхней треугольной, если элементы, стоящие ниже главной диагонали – нули.

Матрицу А называют нижней треугольной, если элементы, стоящие выше главной диагонали – нули.

Матрица А называется симметрической, если она совпадает со своей транспонированной матрицей. Для элементов той матрицы

Теорема: всякую симметрическую матрицу с отличными от нуля главными диагональными минорами всех порядков, можно представить в виде произведения двух треугольных матриц разной структуры, причем единственным образом, если зафиксировать диагональные элементы одной из них.

Следствие: всякую симметрическую матрицу, с отличными от нуля, главными диагональными минорами всех порядков, можно представить в виде произведения двух треугольных матриц, транспонированных по отношению друг к другу, причем единственным образом.

На следствии из теорем базируется метод квадратных корней.

Пусть задана система вида (1’) или (2) с симметрической матрицей А, у которой главные диагональные миноры всех порядков отличны от нуля, тогда по следствию теоремы , где Т – верхняя треугольная матрица

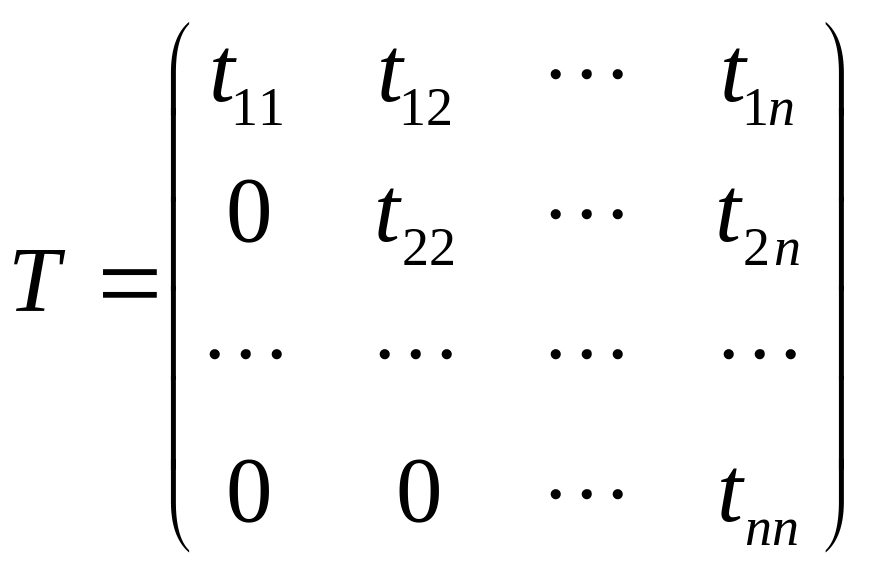
T’ - нижняя треугольная матрица

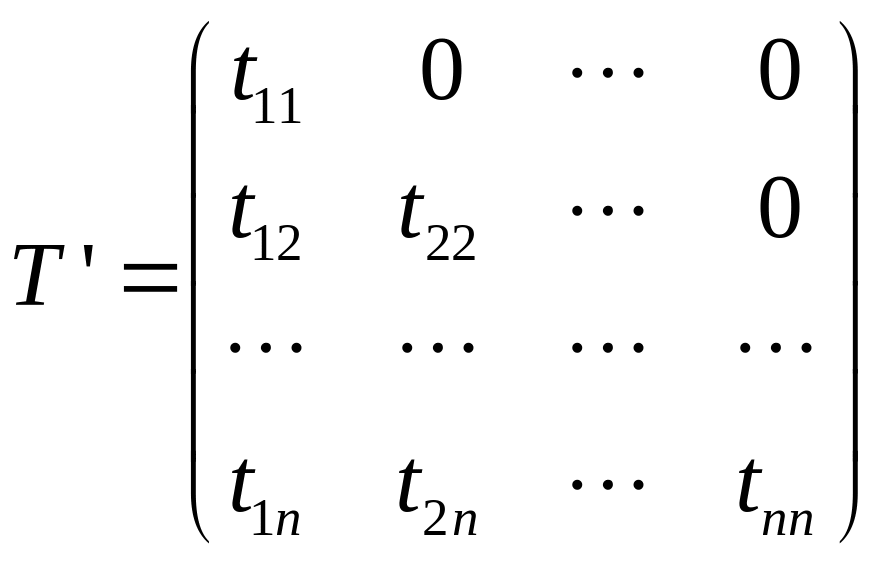
Тогда систему (2) можно записать

(2’)

Обозначим , тогда систему (2) можно записать в виде

То есть решение системы (2) свелось к решению 2х систем (3), (4) треугольного вида.

Суть метода квадратных корней состоит в следующем:

а) заменить матрицу А на матрицы T и T’

б) решить систему ( 3 )

в) решить систему ( 4 )

Метод относится к точным методам, поэтому погрешность метода равна нулю .

Получим расчетные формулы для нахождения матриц и

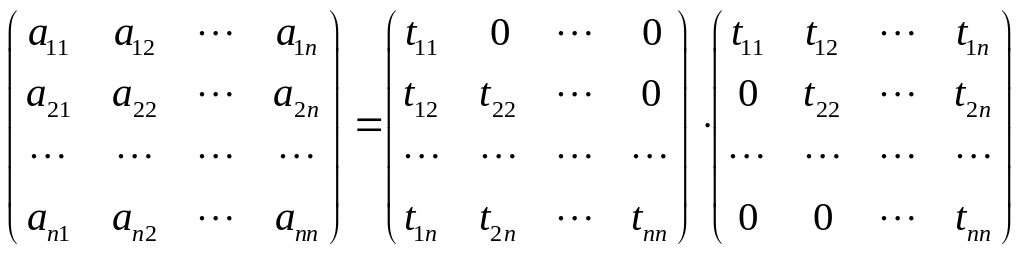
Учитывая предыдущий шаг ,

По аналогии для i-той строки

, откуда при , получим

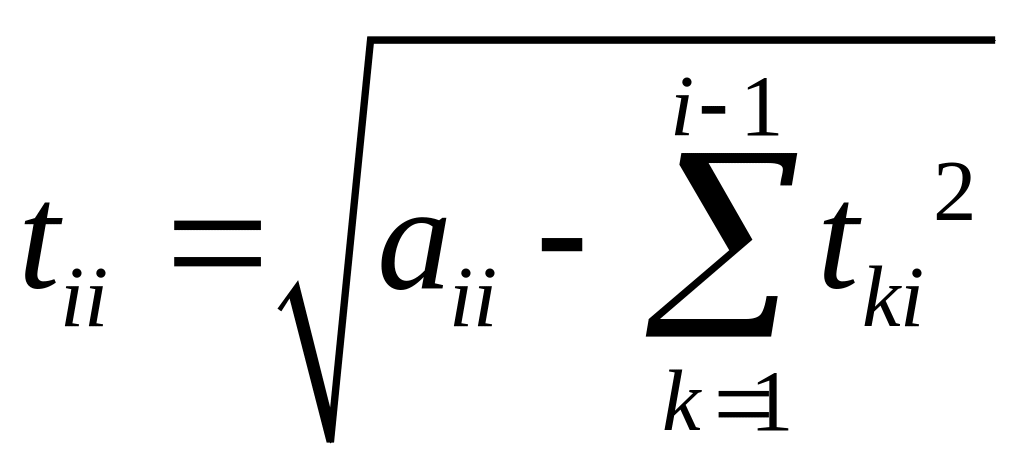
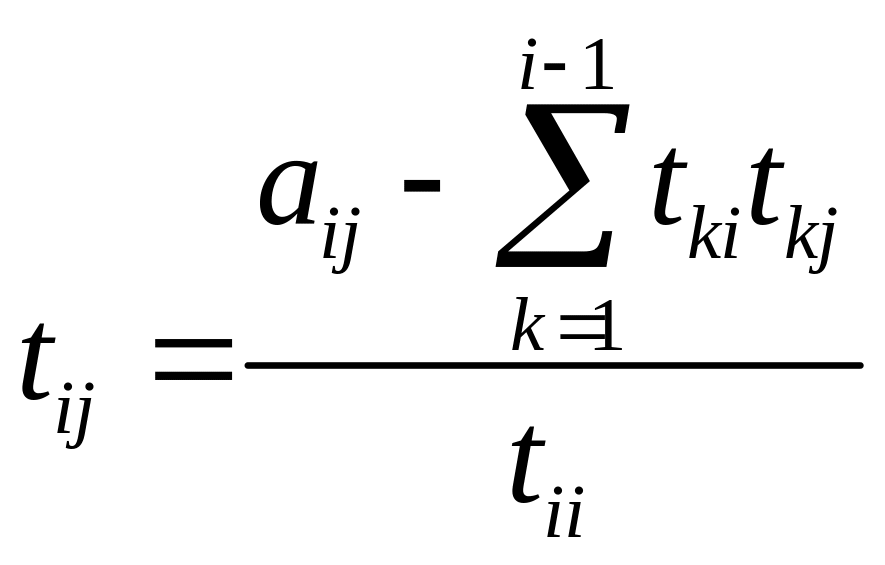
Коэффициенты для матриц и вычисляются по формулам

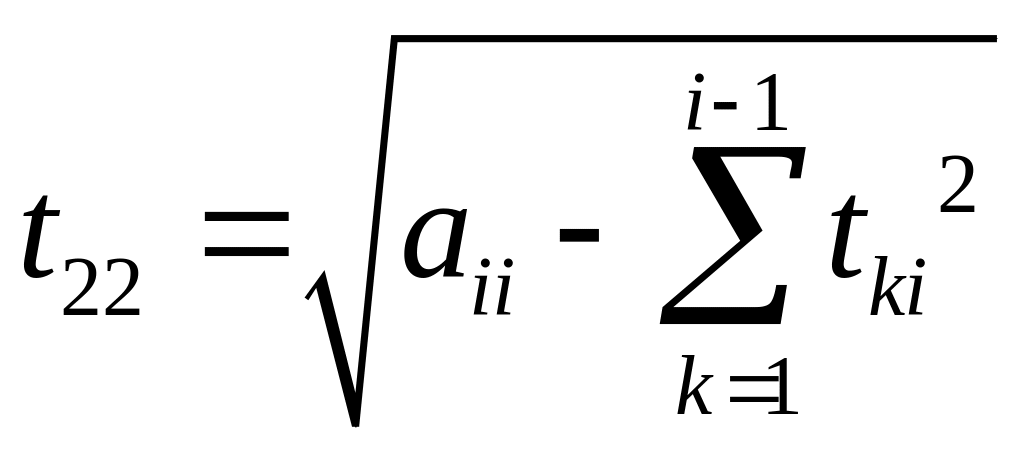
(5)

Решаем систему (3) , где

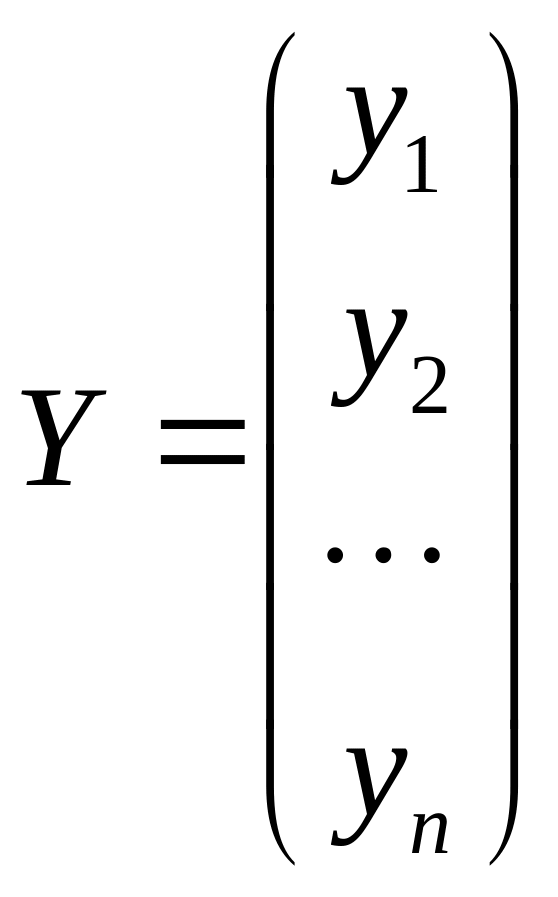
-тое уравнение имеет вид

При получим

Из 2-го уравнения найдем ,

Из -того уравнения найдем ,

, (6)

По формулам (6) находятся элементы вектора Y.

Прямой ход выполнен.

Обратный ход.

Решаем систему ( 4 ), где , матрица Т – верхняя треугольная

-тое уравнение будет иметь вид

При получим, что

Из предыдущего уравнения при получим неизвестное

Из i-того уравнения получим

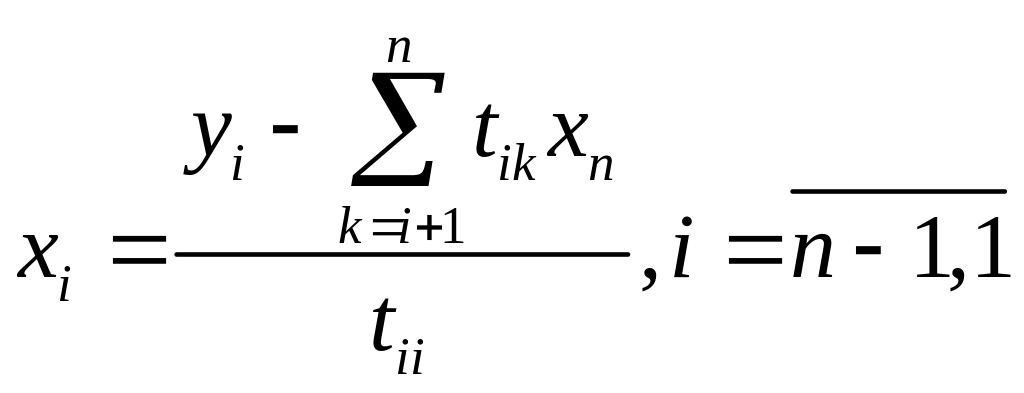(7)

По формулам (7) найдем компоненты вектора X. обратный ход закончен.

Замечание: может оказаться, что для строки s , тогда все коэффициенты этой строки и будут числа мнимые. Метод квадратных корней формально проходит и в этом случае.

Контроль вычислений в методе квадратных корней.

Для контроля вычислений параллельно с системой решается система , где ,

Если над числами выполнять те же действия, что и над числами , то на любом этапе метода квадратных корней в преобразованном уравнении суммы коэффициентов и свободного члена должны давать числа . Это и есть построчный или текущий контроль вычислений.

Окончательный контроль вычислений.

Если - решение системы , а 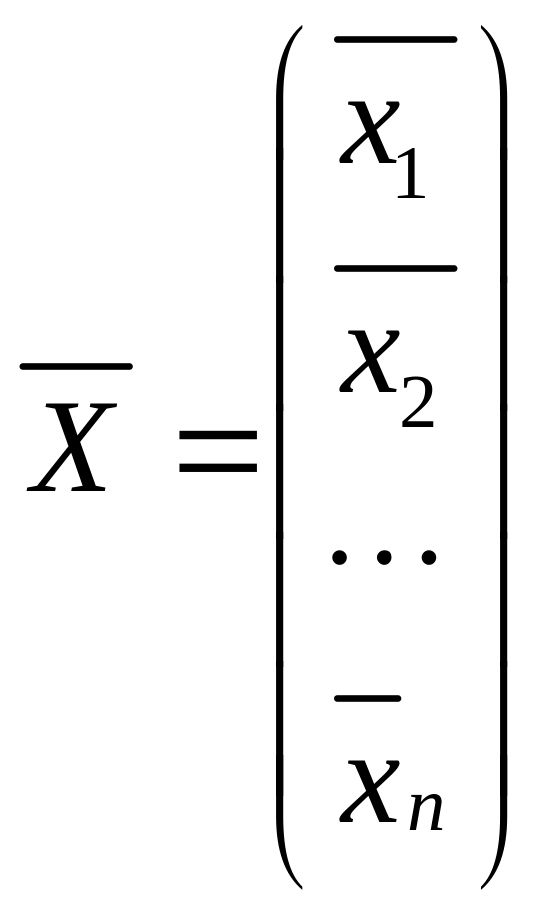- решение системы , то должно выполняться

То есть решения систем должны отличатся на единицу.

Замечание: уточнение корней проводится аналогично, как и в методе Гаусса.