
- •Трофимов в.Г. Методические указания по линейной алгебре (определители, матрицы и системы линейных уравнений)
- •1. Определители
- •1.1 Определители второго и третьего порядков
- •1.2 Свойства определителей
- •Примеры для самостоятельного решения.
- •1.3. Определители высших порядков
- •Примеры для самостоятельного решения.
- •2. Матрицы
- •2.1. Линейные действия с матрицами.
- •Примеры для самостоятельного решения.
- •2.2. Умножение матриц.
- •Примеры для самостоятельного решения.
- •2.3 Обратная матрица.
- •Примеры для самостоятельного решения.
- •3. Системы линейных уравнений.
- •3.1. Формулы Крамера.
- •Примеры для самостоятельного решения.
- •3.2.Решение систем методом обратной матрицы.
- •Примеры для самостоятельного решения. Решить системы с помощью обратной матрицы
- •Решение систем линейных уравнений методом исключения неизвестных (методом Гаусса).
- •Примеры для самостоятельного решения. Решить системы уравнений
- •Однородные системы линейных уравнений
- •Найти все решения следующих однородных систем
- •Примеры для самостоятельного решения. Найти все решения следующих однородных систем
Примеры для самостоятельного решения. Решить системы уравнений
120.
![]() 121.
121.
![]()
122.
![]() 123.
123.
![]()
124.
![]() 125.
125.
![]()
126.
![]() 127.
127.
![]()
128.
![]() 129.
129.
![]()
130.
![]() 131.
131.
![]()
Подобрать λ так, чтобы система уравнений имела решение
132.
![]() 133.
133.
![]()
________________________________________________________________________________
Однородные системы линейных уравнений
Система линейных уравнений (3.1) называется однородной, если все свободные члены b1=b2=…=bn=0. Однородная система всегда обладает тривиальным - нулевым решением: x1= 0, x2= 0,…, xn=0, то есть она всегда совместна.
Пусть дана однородная система трех уравнений с тремя неизвестными
![]()
Могут быть следующие случаи:
а) если определитель системы отличен от нуля, то система имеет единственное решение x1= 0, x2= 0, x3=0;
б) если определитель системы равен нулю, то система имеет бесконечное множество ненулевых решений.
________________________________________________________________________________
Найти все решения следующих однородных систем
Пример 134.
![]()
Решение. Вычислим определитель системы

Поскольку Δ≠0, то данная система имеет единственное решение, которое легко определяется по формулам Крамера. Δ1=Δ2=Δ3=0, отсюда x1= Δ1/Δ=0, x2= Δ2/Δ=0, x3= Δ3/Δ=0. Итак, система имеет только нулевое решение x1= 0, x2= 0, x3=0.
Пример 135.
![]()
Решение. Вычислим определитель системы
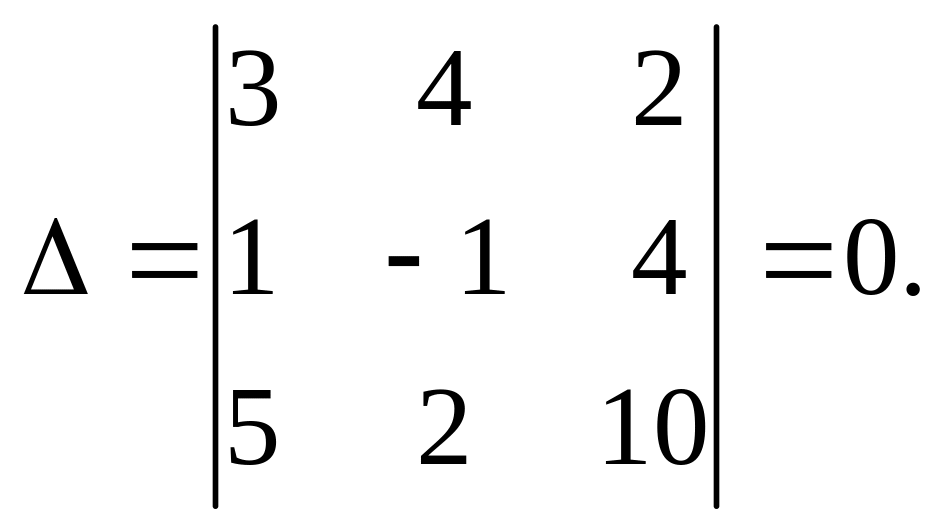
Данная система имеет бесконечное множество решений, так как ее определитель равен нулю. Будем решать систему методом Гаусса.
![]()
Второе и третье уравнения совпали, поэтому имеем систему
![]()
Полагаем x3=α, тогда из второго уравнения вычисляем x2=10α/7 и из первого определяем x1=-18α/7 (α- произвольное число).
Пример 136.
![]()
Решение. Очевидно, система имеет нулевое решение x1= 0, x2= 0, x3=0, x4=0. Исследуем по методу Гаусса данную систему
![]()
Второе и третье уравнения совпали, поэтому имеем систему двух уравнений
![]()
Полагаем x3=α, x4=β. Из из второго уравнения определяем x2=(3α/5)-(7β/5), а из первого определяем x1=(-α/5)-(6β/5), где α и β произвольные числа.
Примеры для самостоятельного решения. Найти все решения следующих однородных систем
137.
![]() 138.
138.![]()
139.
![]() 140.
140.
![]()
141.
![]() 142.
142.
![]()
143.
![]() 144.
144.
![]()
145. При каком значении a система имеет ненулевые решения? Найти их.
а)
![]() б)
б)
![]()
Ответы
4. 60. 5.
5. 6. 1.
7. cos(α+β).
8. sec2α.
9. -(b2+ac).
10. 4ab.
11. (b-c)(d-a).
12. 2b3.
13. -2. 14. -1. 15. -202. 16. -44. 17.
-29. 18. 1. 19. b(b2-a2).
20. 2a2(a+x).
21. 1,-2. 22.
![]() .
23. 0. 24. 0, 2, -2. 25. (4,∞). 26. (-6,-4).
33. Указание. Первую строку умножить
на100, а вторую на 10 и прибавить к третьей
строке по свойству 8. 37. Указание.
воспользоваться свойством 2, переставив
местами первый и второй столбцы последнего
определителя, а затем применить свойство
7. 40. Указание. Применить первое
свойство, затем вынести за знак
определителя множители (-1) из всех трех
строк. 43. Равенство несправедливо.
44. Равенство справедливо. Указание.
Применить свойство 7 по столбцам. 45.
.
23. 0. 24. 0, 2, -2. 25. (4,∞). 26. (-6,-4).
33. Указание. Первую строку умножить
на100, а вторую на 10 и прибавить к третьей
строке по свойству 8. 37. Указание.
воспользоваться свойством 2, переставив
местами первый и второй столбцы последнего
определителя, а затем применить свойство
7. 40. Указание. Применить первое
свойство, затем вынести за знак
определителя множители (-1) из всех трех
строк. 43. Равенство несправедливо.
44. Равенство справедливо. Указание.
Применить свойство 7 по столбцам. 45.
![]() 46. Δ. 47. Да. 48. а) -20, б) 18, в) -4. 49.
-31 50. 180. 51. 87. 52. 0. 53. 72.
54. (y-x)(z-x)(z-y).
57. 12. 58. 180. 59. 48. 60. 1. 61.
Нет. 64.
46. Δ. 47. Да. 48. а) -20, б) 18, в) -4. 49.
-31 50. 180. 51. 87. 52. 0. 53. 72.
54. (y-x)(z-x)(z-y).
57. 12. 58. 180. 59. 48. 60. 1. 61.
Нет. 64.
![]() .
65.
.
65.
![]() .
66.
.
66.
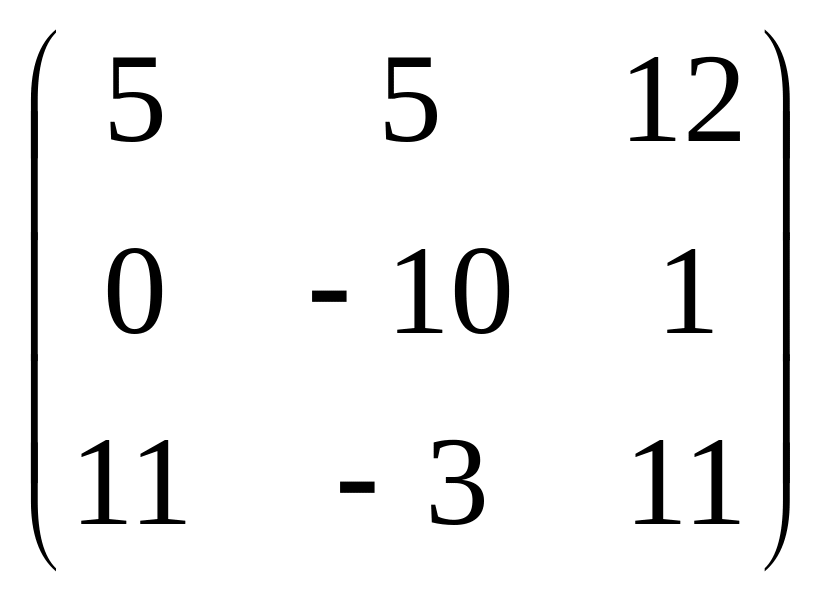 .
67.
.
67.
 .
71.
.
71.
![]() 72.
72.
![]() 73.
73.
 74. (13). 75.
74. (13). 75.
![]() 76.
76.
![]() .
77.
.
77.
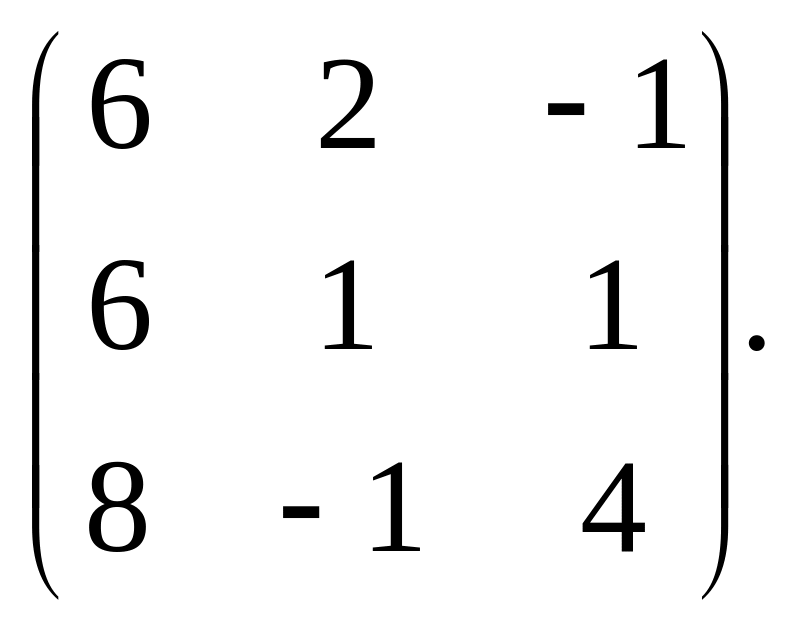 78.
78.
 81.
81.
 85.
85.
![]() 86.
86.
![]() 87.
87.
![]() 88.
88.
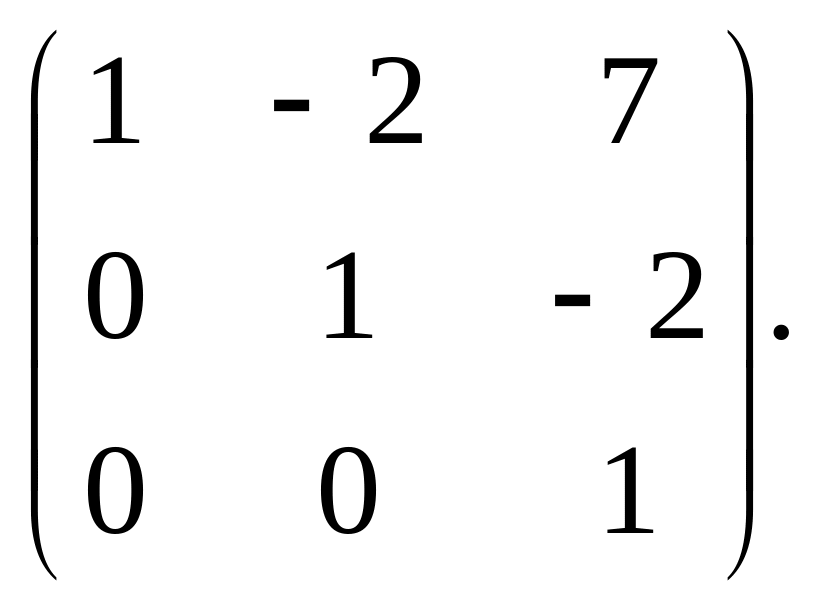 89.
89.
 90.
90.
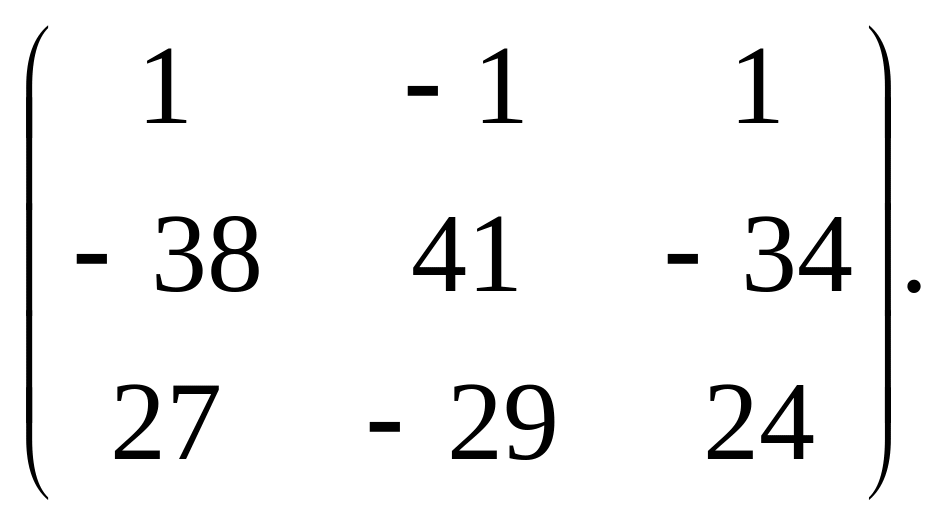 91.
91.
![]() 92.
92.
![]() 93.
93.
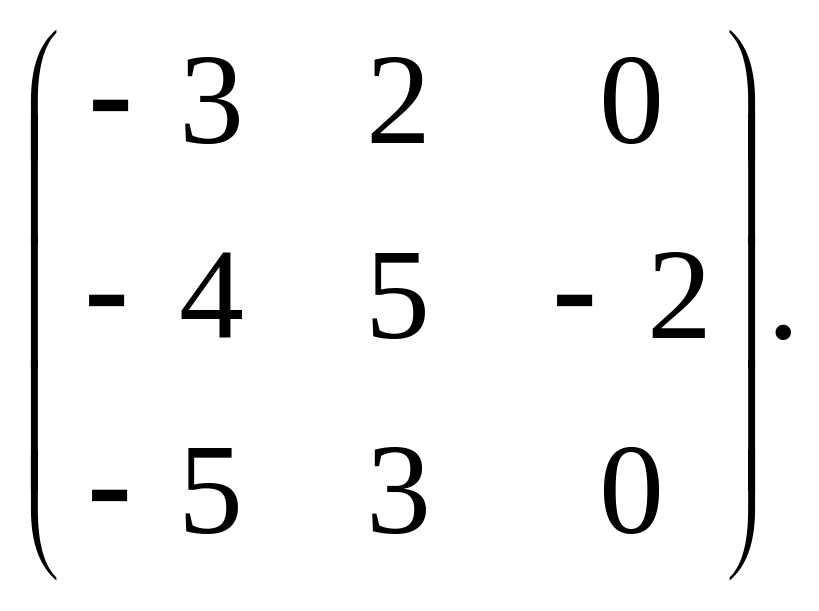 94.
94.
 95.
95.
![]() 96.
96.
![]() 97. В матрице A-1
поменяются местами соответствующие
столбцы и перед матрицей появится
множитель (-1). 100. (3,-1). 101. (3,-1). 102.
(-2,-1). 103. (-2,-1). 104. (1,1,1). 105.
(2,3,1). 106. (3,1,1). 107. (-1,-1,0,1). 110.
(2,-5). 111. (2,-5). 112. (3,1,1). 113. (3,1,1).
114. (2,1,3). 115. (1,2,-5). 120. (1,2,-2). 121.
Система имеет бесчисленное множество
решений: x1=1,
x2=-2(1+α),
x3= α,
где α-любое произвольное
число. 122. Система решений не имеет.
123. Система имеет бесчисленное
множество решений: x1=-3-2α,
x2=4+α,
x3= α.
124. Система решений не имеет. 125.
(1,2,-2). 126. (3,4,5). 127. Система имеет
бесчисленное множество решений: x1=2α-β,
x2=α,
x3= β, x4=1,
где α и β - произвольные
числа. 128. Система решений не имеет.
97. В матрице A-1
поменяются местами соответствующие
столбцы и перед матрицей появится
множитель (-1). 100. (3,-1). 101. (3,-1). 102.
(-2,-1). 103. (-2,-1). 104. (1,1,1). 105.
(2,3,1). 106. (3,1,1). 107. (-1,-1,0,1). 110.
(2,-5). 111. (2,-5). 112. (3,1,1). 113. (3,1,1).
114. (2,1,3). 115. (1,2,-5). 120. (1,2,-2). 121.
Система имеет бесчисленное множество
решений: x1=1,
x2=-2(1+α),
x3= α,
где α-любое произвольное
число. 122. Система решений не имеет.
123. Система имеет бесчисленное
множество решений: x1=-3-2α,
x2=4+α,
x3= α.
124. Система решений не имеет. 125.
(1,2,-2). 126. (3,4,5). 127. Система имеет
бесчисленное множество решений: x1=2α-β,
x2=α,
x3= β, x4=1,
где α и β - произвольные
числа. 128. Система решений не имеет.
129. (1,2,-2). 130. (1,2,1). 131. Система имеет бесчисленное множество решений: x1=(-11α)/7, x2=-α/7, x3= α. 132. 5. 133. -6. 137. (0,0,0). 138. x1=-4α, x2=-α, x3= 5α, где α- произвольное число. 139. x1=2α-3β, x2=α, x3= β. 140. x1=-3α, x2=10α/7, x3= α. 141. (0,0,0). 142. (0,0,0). 143. Система имеет бесчисленное множество решений: x1=-α+7β/6, x2=α+5β/6, x3= α, x4= β/3, x5= β. 144. Система имеет бесчисленное множество решений: x1=α, x2=-2α, x3= α. 145. а) При a=0: x1=α, x2=0, x3= 0; при a=2: x1=5α, x2=-8α, x3= 2α; б) при a=0: x1=α x2=α, x3= α.
________________________________________________________________________________
