Тема 2.3. Интегральное исчисление.

1. Понятие неопределенного интеграла и его свойства.

2. Формулы интегрирования.

3. Методы интегрирования неопределенного интеграла.

4. Определенный интеграл и его свойства. Формула Ньютона-Лейбница.

5. Методы интегрирования определенного интеграла.

6. Приложения интеграла.

Пункт 1. Понятие неопределенного интеграла и его свойства.

Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном или бесконечном), если в каждой точке этого интервала f(x) является производной для F(x), т.е. . Из этого определения следует, что задача нахождения первообразной обратна задаче дифференцирования: по заданной функции f(x ) требуется найти функцию F(x), производная которой равна f(x). Основное свойство первообразной: множество первообразных функции f(x) (т.е. функций, имеющих производную f(x) и дифференциал f(x) dx) на этом интервале описывается выражением F(x) + C, где C - произвольная постоянная.

Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом . Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то , где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.

• Свойства неопределённого интеграла:

1. .

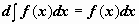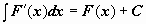2. (или ).

3. ();

4. ;

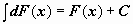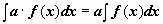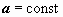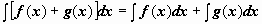Пункт 2. Формулы интегрирования.

1	.	11	.
2	.	12	.
3	().	13	.
4	.	14	.
5	; .	15	.
6	.	16
7	.	17	.
8	.	18	.
9	.	19	.
10	.	20	; .

Пункт 3. Методы интегрирования.

Существует три основных метода интегрирования: Непосредственное интегрирование, метод замены переменной или метод подстановки и интегрирование по частям.

Рассмотрим каждый из этих методов подробнее.

Непосредственное интегрирование. Суть этого метода заключается в интегрировании с помощью основных свойств неопределенного интеграла, преобразования подынтегрального выражения с помощью тождественных преобразований к табличным интегралам.

Примеры.

1. .

2. 

3. 

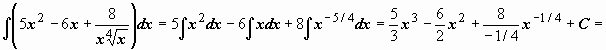
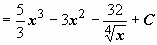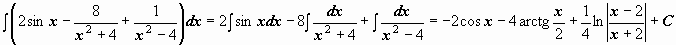
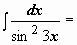
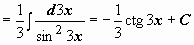
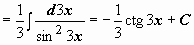
Метод замены переменной или метод подстановки. Суть данного метода заключается в том, что он позволяет с помощью введения новой переменной свести данный интеграл к новому интегралу, который сравнительно легко берется непосредственно.

Существует некоторый алгоритм, который помогает вычислить неопределенный интеграл методом замены переменной:

1. часть подынтегральной функции надо заменить новой переменной;

2. найти дифференциал от обеих частей замены;

3. всё подынтегральное выражение выразить через новую переменную, после чего должен получиться табличный интеграл;

4. найти полученный табличный интеграл;

5. сделать обратную замену.

Примеры.

Метод интегрирования по частям. Данный метод осуществляется при использовании формулы , где u, - непрерывно-дифференцируемые функции от х.

При вычислении интеграла этим методом подынтегральное выражение f(x)dx представляется в виде произведения множителей u и ; при этом dx обязательно входит в . В результате получается, что заданный интеграл находят по частям: сначала находят , а затем .

Алгоритм Представляют интеграл через u и с помощью таблицы
 
	интеграл вида:					интеграл вида:
 
замена					замена
Примечание:		Интегрирование по частям применяется в том случае, если под знаком интеграла стоят произведения: степенной и тригонометрической функций; степенной и обратной тригонометрической функций; степенной и логарифмической функций; степенной и показательной функций.

Примеры:

11. .

12. .

13. 

.

14. ==

15. ==

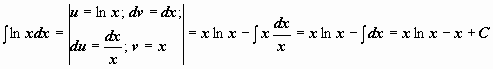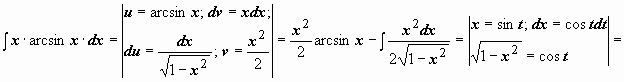
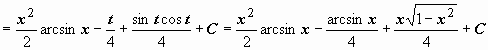Пункт 4. Определенный интеграл и его свойства. Формула Ньютона-Лейбница.

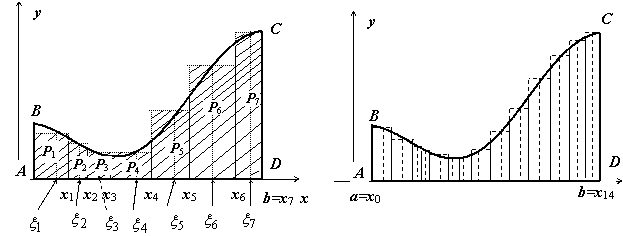
Пусть на отрезке [a,b] (b>a) задана непрерывная функция y = f(x) , принимающая на этом отрезке неотрицательные значения : при . Требуется определить площадь S криволинейной трапеции ABCD, ограниченной снизу отрезком [a,b], слева и справа - прямыми x = a и x = b, сверху – функцией y = f(x).

Для решения этой задачи разделим произвольным образом основание AD фигуры точками x₀ = a, x₁ , x₂ , …, x_n-1 = a, x_n = b на n частей [x₀ , x₁], [x₁ , x₂], …, [x_i-1 , x_i], …, [x_n-1 , x_n]; символом будем обозначать длину i-го отрезка: . На каждом из отрезков [x_i-1 , x_i] выберем произвольную точку , найдём , вычислим произведение (это произведение равно площади прямоугольника P_i с основанием [x_i-1 , x_i] и высотой ) и просуммируем эти произведения по всем прямоугольникам. Полученную сумму обозначим S _ступ: .

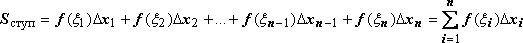S_ступ равно площади ступенчатой фигуры, образованной прямоугольниками P_i , i = 1,2,…,n; на левом рисунке эта площадь заштрихована. S_ступ не равна искомой площади S, она только даёт некоторое приближение к S. Для того, чтобы улучшить это приближение, будем увеличивать количество n отрезков таким образом, чтобы максимальная длина этих отрезков стремилась к нулю (на рисунке ступенчатые фигуры изображены при n = 7 (слева) и при n = 14 (справа)). При разница между S_ступ и S будет тоже стремиться к нулю, т.е. .

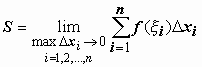Пусть на отрезке [a,b] задана функция y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x₀ , x₁], [x₁ , x₂], …, [x_i-1 , x_i], …, [x_n-1 , x_n]; длину i-го отрезка обозначим : ; максимальную из длин отрезков обозначим . На каждом из отрезков [x_i-1 , x_i] выберем произвольную точку и составим сумму 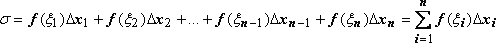. Сумма называется интегральной суммой.

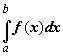Предел последовательности интегральных сумм при , не зависящий ни от способа разбиения отрезка [a,b] на части [x_i-1 , x_i], ни от выбора точек , называется определённым интегралом от функции f(x) по отрезку [a,b] и обозначается , где функция f(x) называется подынтегральной, числа a и b - соответственно, нижним и верхним пределами интегрирования.

.
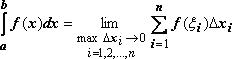