15.2. Основные характеристики поведения функции.

К основным характеристикам поведения функции относятся: нули функции и интервалы знакопостоянства, четность или нечетность, периодичность, монотонность (убывание и возрастание) и экстремумы (максимумы и минимумы), выпуклость или вогнутость и точки

перегиба, ограниченность и наибольшее и наименьшее значения, асимптоты.

Дадим определения некоторых основных характеристик поведения функции, известные из элементарной математики, другие же будем вводить по мере необходимости и расширения арсенала методов исследования.

1. Нули функции. Нулями функции y=f(x) называются корни уравнения f(x)=0, т.е. значения аргумента х, при которых функция обращается в нуль. Другими словами, нуль функции – это точка в которой график функции пересекает ось Ох (см. рис. 15.2.).

х₁, х₂– нули функции,

f(x₁)=0, f(x₂)=0.

2. Четность, нечетность.

Функция y=f(x), х(-а, а) называется четной, если х(-а, а)

f(-x)=f(x).

График четной функции симметричен относительно оси Оу (см. рис. 15.3).

Функция y=f(x), х (-а, а) называется нечетной если для х(-а, а)

f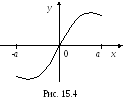(-x)=-f(x).

График нечетной функции симметричен относительно начала координат (см. рис. 15.4).

Функция может быть ни четной, ни нечетной, т.е. общего вида.

3. Периодичность. Функция y=f(x) называется периодической, если существует такое число а>0, что для любого х справедливо равенство

f(x+а)= f(x).

Наименьшее положительно число а, для которого выполняется вышеприведенное равенство, называется периодом функции и обозначается буквой Т. Тогда х пZ

f(x+nT)= f(x).

Поведение периодической функции достаточно изучить на промежутке, длина которого равна периоду функции, например на отрезке [0, T], где Т– период. График периодической функции получается путем повторения части графика, построенного на отрезке длины, равной периоду функции.

Р ассмотрим функцию у=sin x, имеющую период Т=2. Построив график этой функции на промежутке [-, ], мы легко распространим его на всю числовую ось (см. рис. 15.5):

Найдем период функции у=sin ax, где а– положительное число. Так как

sin ax=sin (ax+2)=sin [a(x+)],

то по определению период функции у=sin x равен , что геометрически означает сжатие графика к оси Оу в а раз при а>1 и растяжение графика от оси Оу при а<1.

4. Монотонные функции. Важными характеристиками поведения функции являются возрастание и убывание.

Функция y=f(x) называется возрастающей в интервале (a, b), если большему значению аргумента соответствует большее значение функции, другими словами, еслих₁, х₂ (a, b)

(x₁<x₂) => (f(x₁)<f(x₂).).

При возрастании аргумента график возрастающей функции поднимается вверх (см. рис. 15.6).

Функция y=f(x) называется убывающей в интервале (a, b), если большему значению аргумента соответствует меньшее значение функции, другими словами, еслих₁, х₂ (a, b)

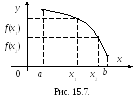(x₁<x₂) => (f(x₁)>f(x₂).).

При возрастании аргумента график убывающей функции опускается вниз (см. рис. 15.7).

На рис. 15.5. изображен график у=sin x. На интервале функция возрастает, а на интервале она убывает.

5. Ограниченность функции.

Ограниченность y=f(x) с областью определения X_f называется ограниченной сверху, если множество ее значений Y_f ограничено сверху, т.е. существует число М такое, что f(x)M для х X_f. Пусть M_f=sup Y_f – точная верхняя граница значений функции, тогда f(x)M_f xX_f.

Функция у=f(x), хX_f, называется ограниченной снизу, если множество ее значений Y_f ограничено снизу, т.е. существует число m такое, что mf(x) х X_f. Пусть m_f=inf Y_f– точная нижняя граница значений функции, тогда m_ff(x) х X_f.

Функция y=f(x) хX_f , называется ограниченной, если она ограничена сверху и снизу. В этом случае m_f f(x) M_f х X_f. Условия ограниченности функции f(x) можно записать в следующем виде:

(f(x) ограничена)  (M>0 х X_f |f(x)| М).

В качестве примера рассмотрим функцию y=sin x, ограниченную на всей числовой оси: |sin x| 1, а ее график заключен между прямыми у=1 (см. рис. 15.5).

Наибольшим значением функции y=f(x), х X_f, называется наибольший элемент множества значений Y_f , обозначим его М: М=mах Y_f и найдется значение аргумента x₁ X_f такое, что f(x₁)=М. Ясно, что тогда М=М_f=sup Y_f .

Наименьшим значением функции y=f(x), х X_f, называется наименьший элемент множества значений Y_f , обозначим его m: т=min Y_f и найдется значение аргумента x₂ X_f такое, что f(x₂)=m. Ясно, что тогда m=m_f=inf Y_f .

Пример 15.1. Рассмотрим функцию у=х² с областью определения Х_f =[0,1] и областью значений Y_f=[0,1] (см. рис. 15.8а).

Н аибольшее значение М=1=f(1)=M(f), наименьшее значение m=0=f(0)=m_f.

Если же у =х² и X_f =[0,1), то Y=[0,1) (см. рис. 15.8б). Тогда, как и выше, функция у=х² принимает наименьшее значение m=0=f(0)=m_f . Однако наибольшее значение функция не имеет, но ограничена сверху и М_f=1.