5.2. Дисперсия случайной величины

Определение. Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:

D(X) = M[X – M(X)]2.

(5.9)

Для дискретной случайной величины X эта формула принимает вид:

.

(5.10)

Для непрерывной случайной величины:

.

(5.11)

На практике для вычисления дисперсии часто удобно пользоваться следующей теоремой.

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:

D(X) = M(X2)– [M(X)]2.

(5.12)

Для дискретной случайной величины X эта формула принимает вид:

.

(5.13)

Для непрерывной случайной величины:

.

(5.14)

Рассмотрим свойства дисперсии.

1. Дисперсия постоянной величины равна нулю:

D(С) = 0.

(5.15)

2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.

D(kX) = k2D(X).

(5.16)

3. Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.

D(X + Y) = D(X) + D(Y).

(5.17)

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.

D(X – Y) = D(X) – D(Y).

(5.18)

Пример 5.2. Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.

Решение. Используя свойства дисперсии, находим

D(Z) = 8²D(X) – 5²D(Y) + D(7) = 64·1 + 25·2 + 0 = 114. ◄

5.3. Среднее квадратическое отклонение случайной величины

Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину .

Определение. Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:

.

(5.19)

Свойства среднего квадратического отклонения вытекают из свойств дисперсии.

5.4. Мода и медиана. Квантили

Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.

Определение.Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение(для которого вероятностьp_iили плотность вероятностиf(x) достигает максимума).

Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.

Определение.Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого

Р(Х < Ме(Х)) = Р(Х > Ме(Х)) =

(5.20)

т. е. вероятность того, что случайная величина Хпримет значение, меньшее медианы или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямаях=Ме(Х), проходящая через точку с абсциссой, равнойМе(Х), делит площадь фигуры под кривой распределения на две равные части. Очевидно, что в точкех=Ме(Х) функция распределения равна 1/2.

Пример 5.3.Найти моду, медиану случайной величиныХс плотностью вероятностиf(x) = 3х²прих[0; 1].

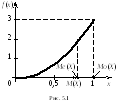Решение.Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна прих=Мо(Х) = 1.

Медиану Ме(Х) = найдем из условия (5.20):

,

или

,

откуда .◄

Наряду с модой и медианой для описания случайной величины используется понятие квантиля.

Определение.Квантилем уровняq(илиq-квантилем)называется такое значение х_q случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.

F(хq) = P(X < хq) = q.

(5.21)

Пример 5.4.По данным примера 5.3 найти квантильх_0,3.