1) ; И, 2).

Формулы общего характера

1. Пусть 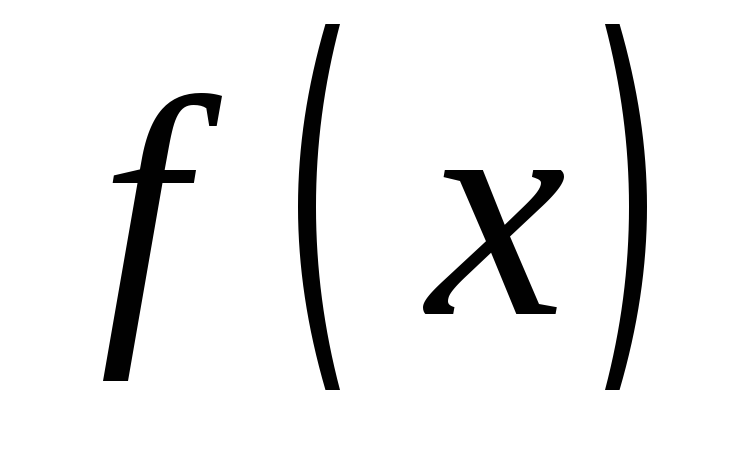— функция, интегрируемая на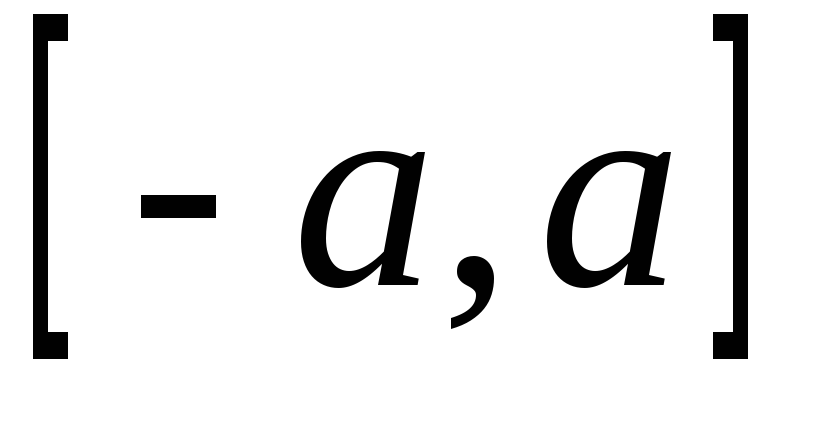, и удовлетворяющая на этом отрезке соотношению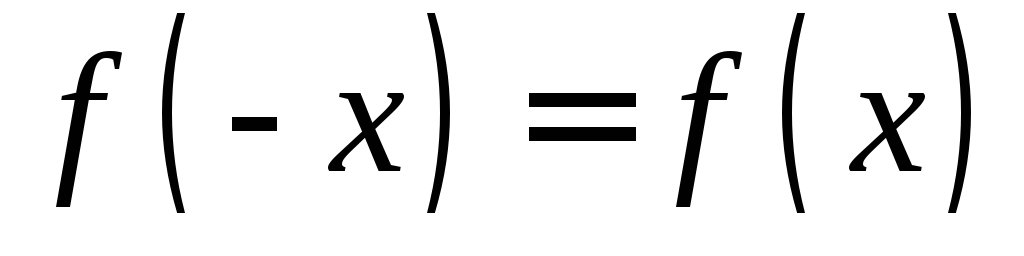(такую функцию называют четной); тогда

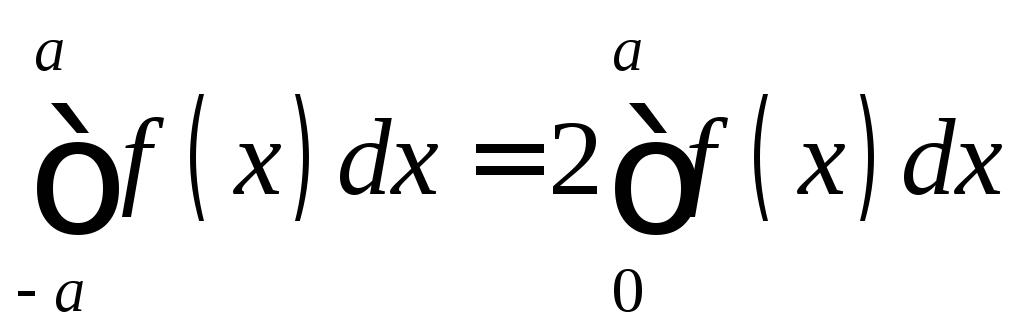
2. Пусть 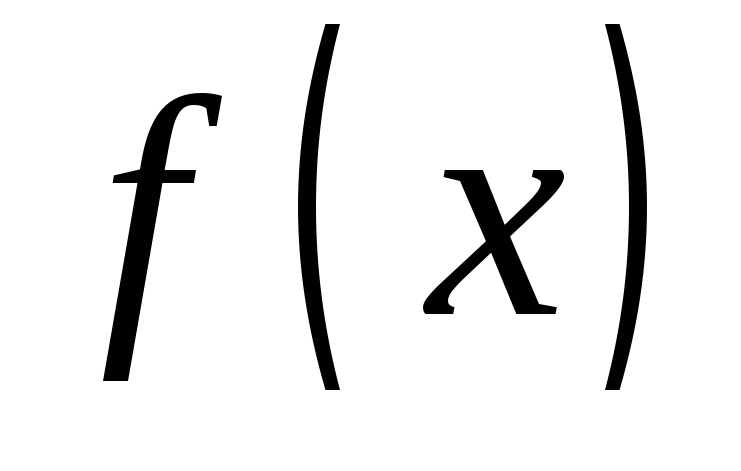— функция, интегрируемая на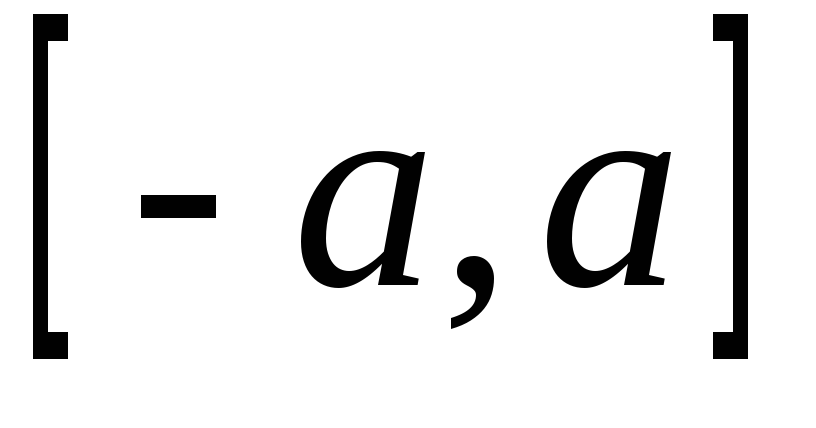, и удовлетворяющая на этом отрезке соотношению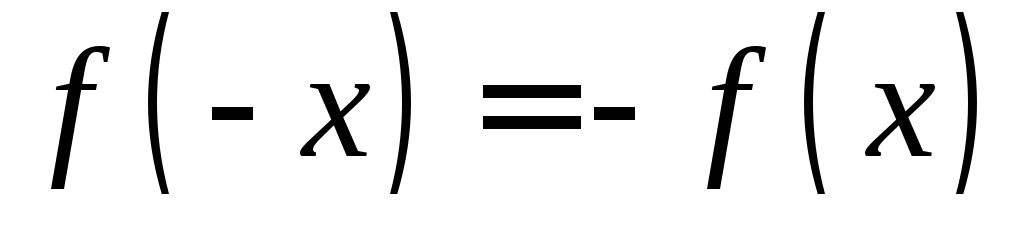(такую функцию называют нечетной); тогда

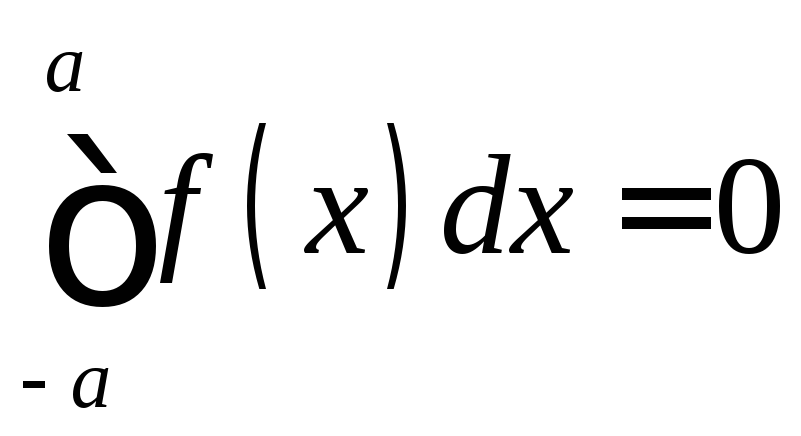
Замена переменного в определенном интеграле

Формула

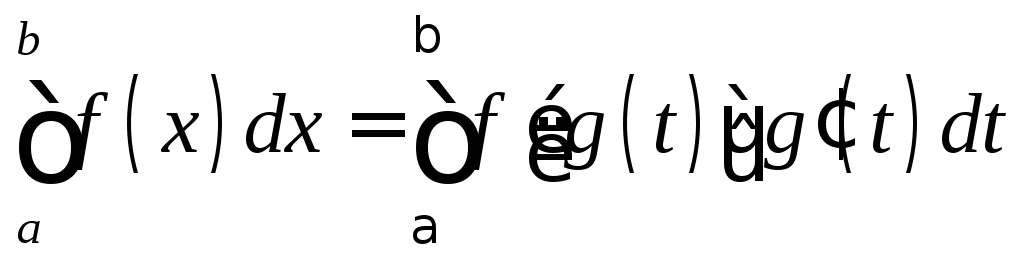
действительна при следующих условиях:

1. Функция 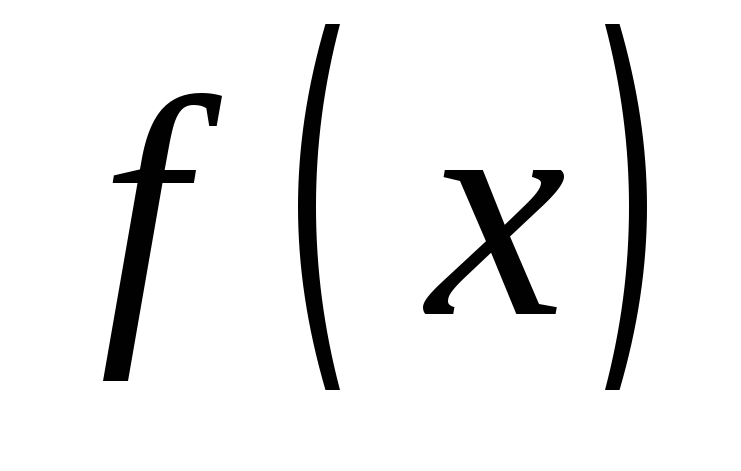непрерывна на отрезке;

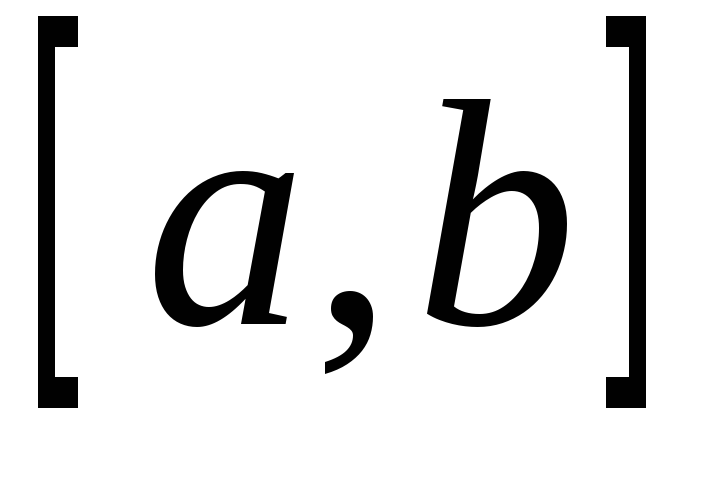2. Отрезок 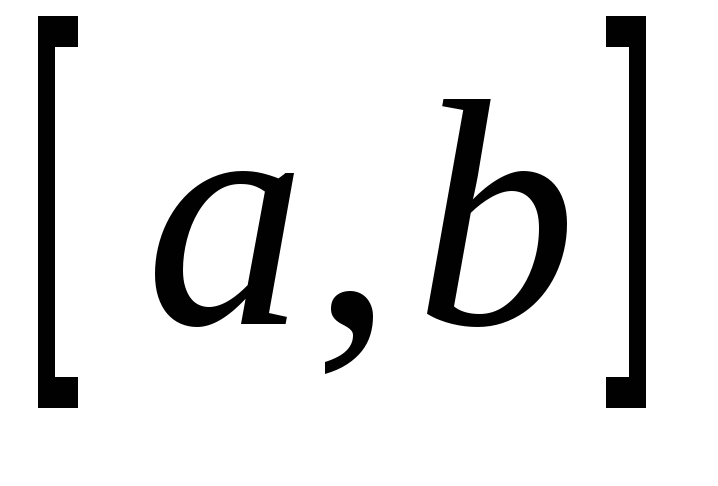является множеством значений функции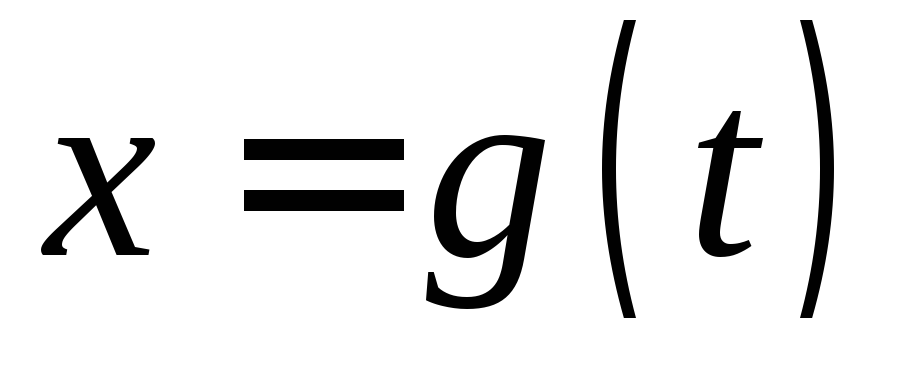, определенной на отрезке;

3. ; .

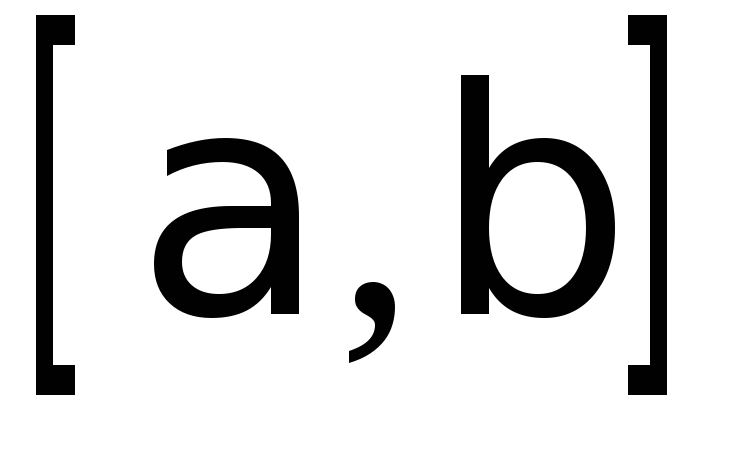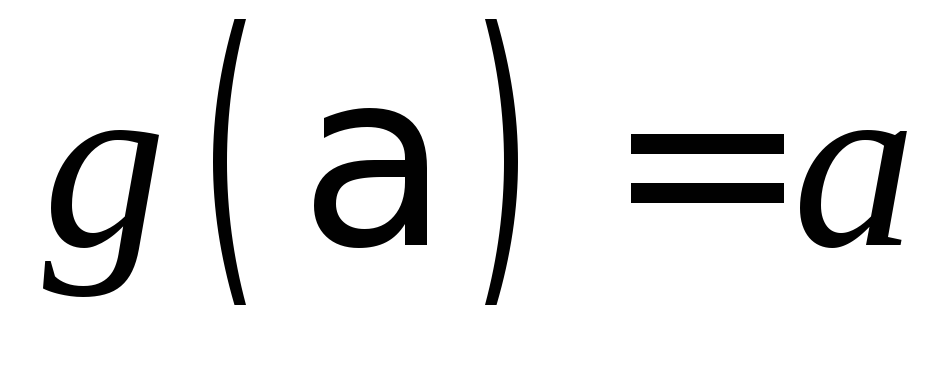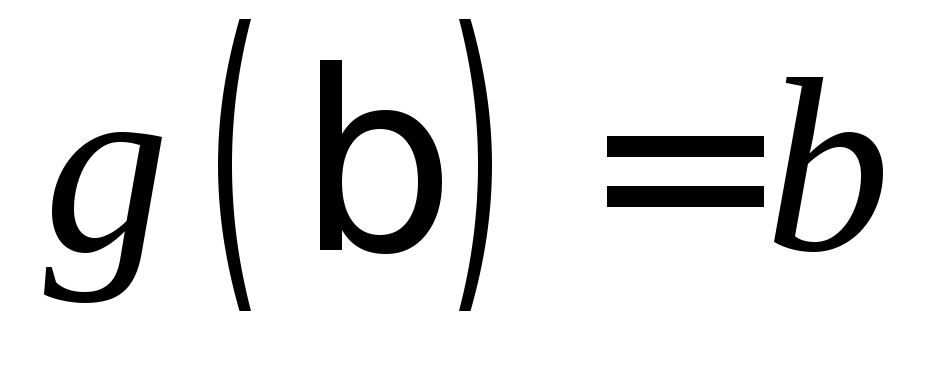Формула интегрирования по частям

Если каждая из функций иимеет на отрезкенепрерывную производную, то справедлива следующая формула

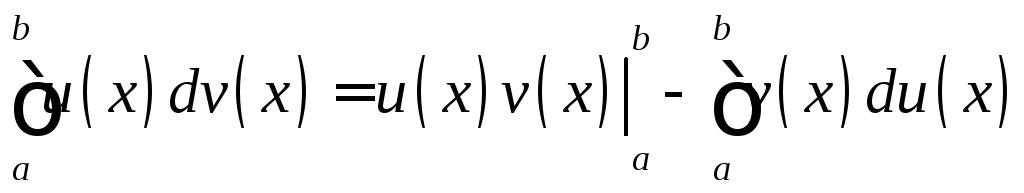
Геометрические приложения определенного интеграла

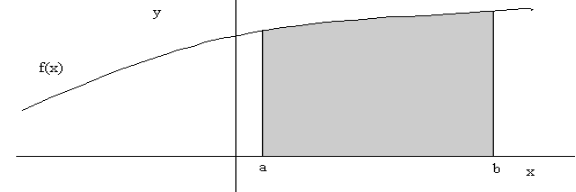
1. Площадь криволинейной трапеции

Площадь фигуры, называемой криволинейной трапецией, лежащей под графиком и неотрицательной на отрезкеравна

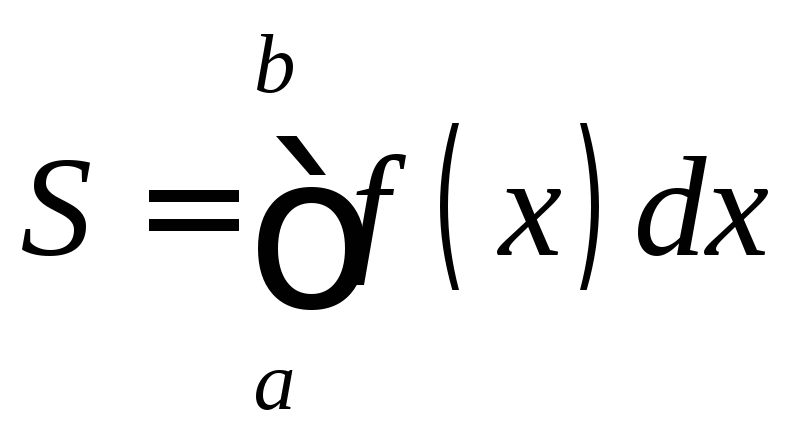
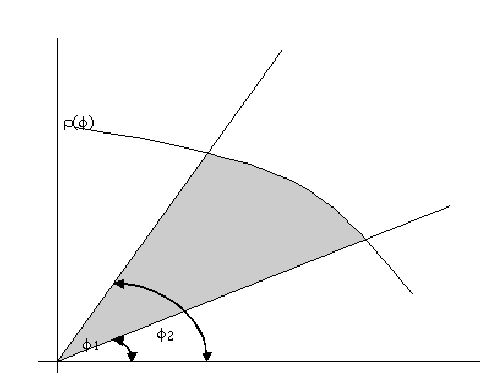
2. Площадь криволинейного сектора

Площадь фигуры, называемой криволинейным сектором, ограниченной графиком и двумя лучами, составляющими с полярной осью углыиимеет площадь

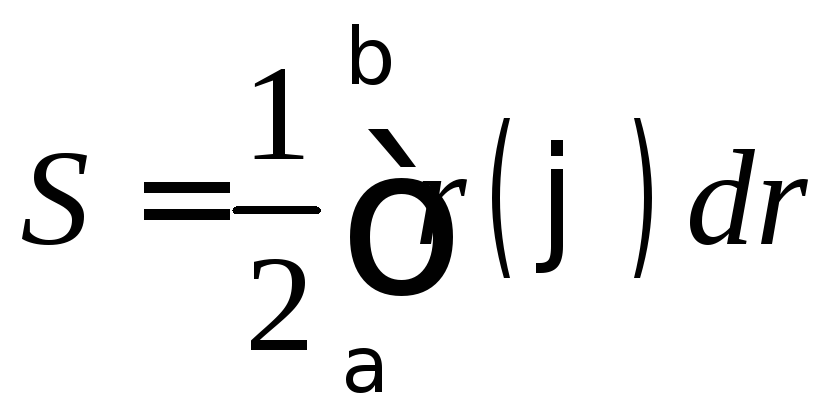
3. Вычисление объема вращения

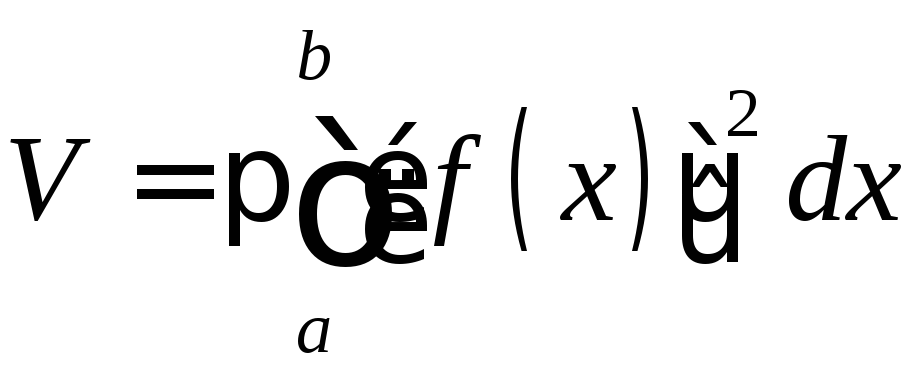
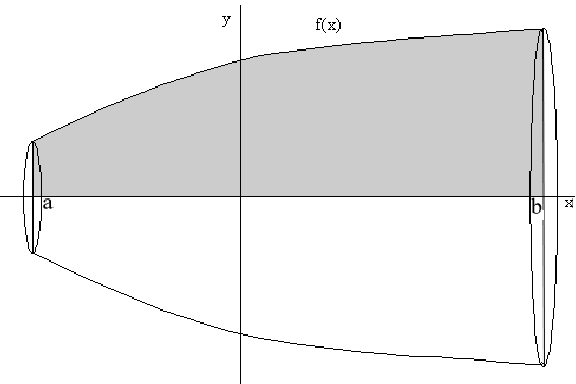
4. Длина дуги кривой.

Если плоская кривая L задана параметрически

, ,

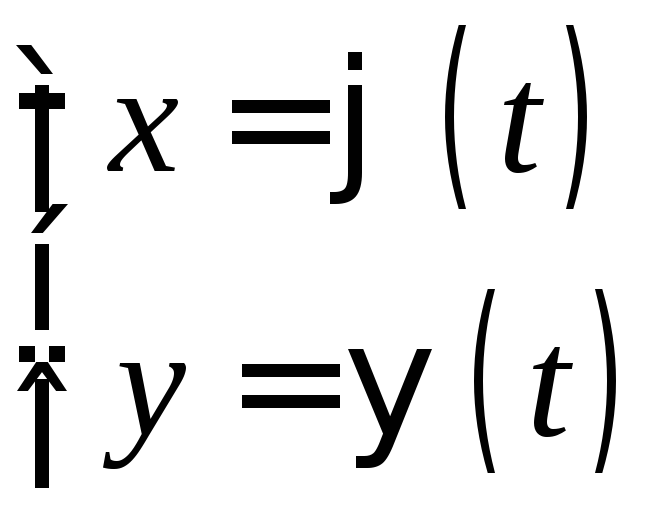причем и- непрерывно дифференцируемые функции, то она имеет длину, вычисляемую по следующей формуле

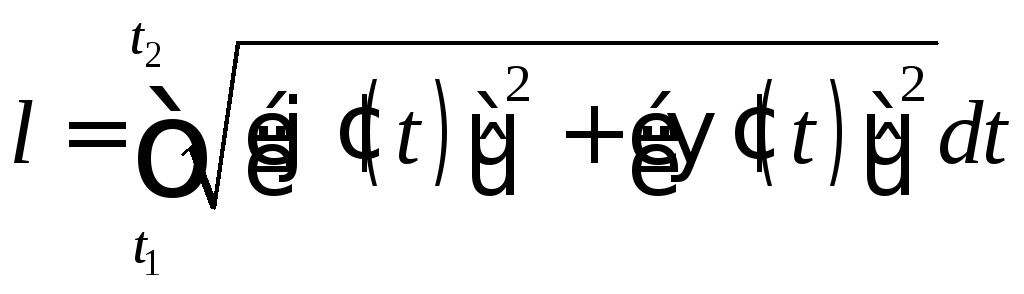
Если плоская кривая L – график непрерывно дифференцируемой функции и, то длина этой кривой вычисляется по формуле

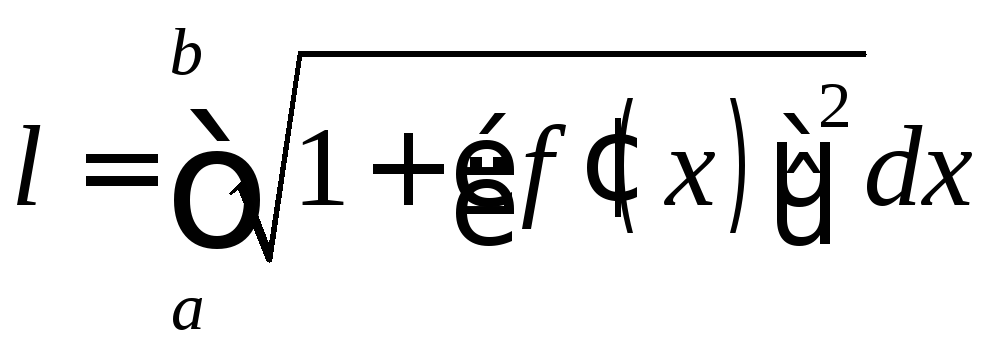
В полярных координатах

Примеры

Задача 1.Вычислить интеграл:

.

Решение: применяя интегрирование по частям, получаем

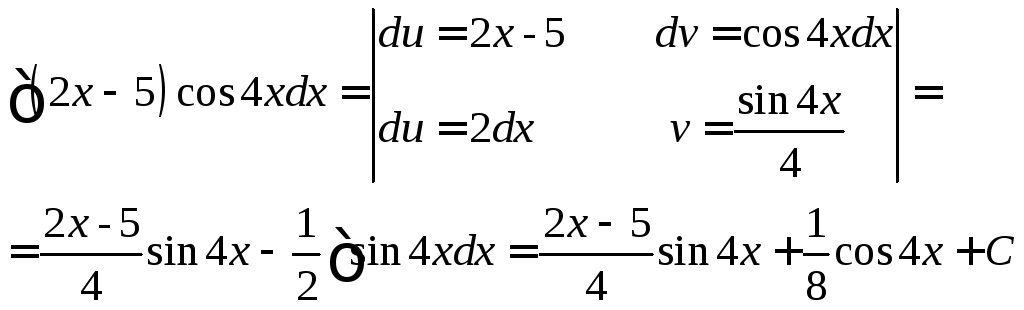
Задача №2:

Вычислить интеграл: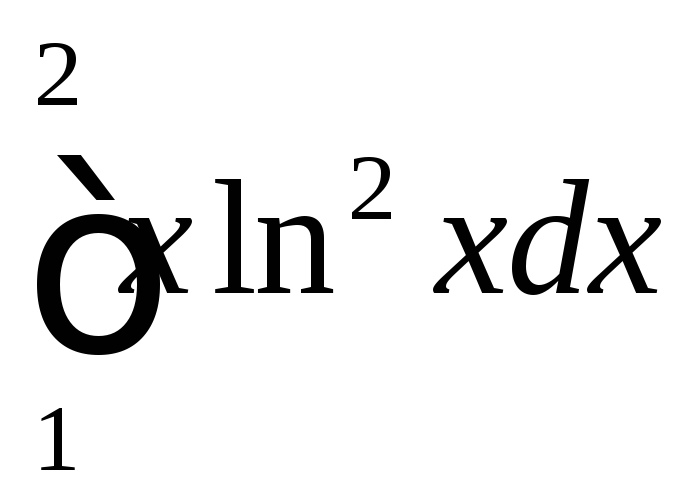

Решение:

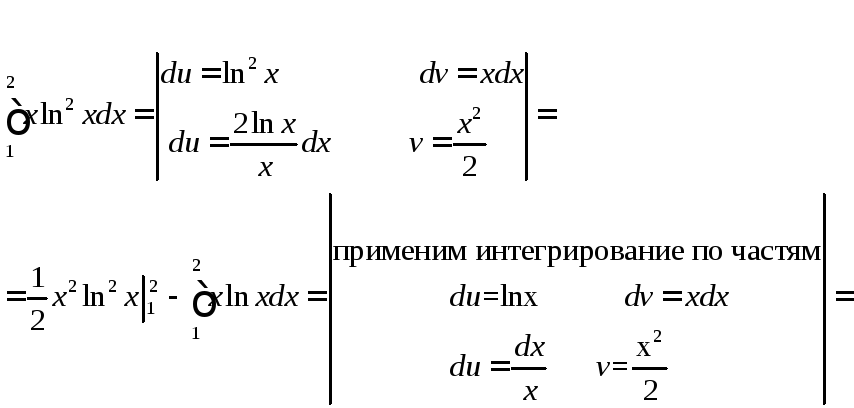
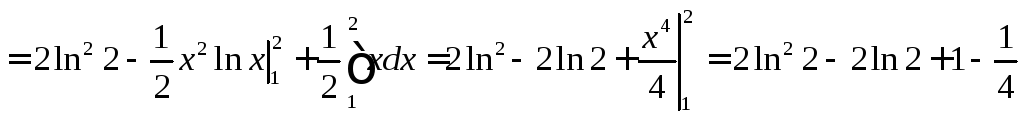
Задача №3:

Вычислить интеграл:

Решение:

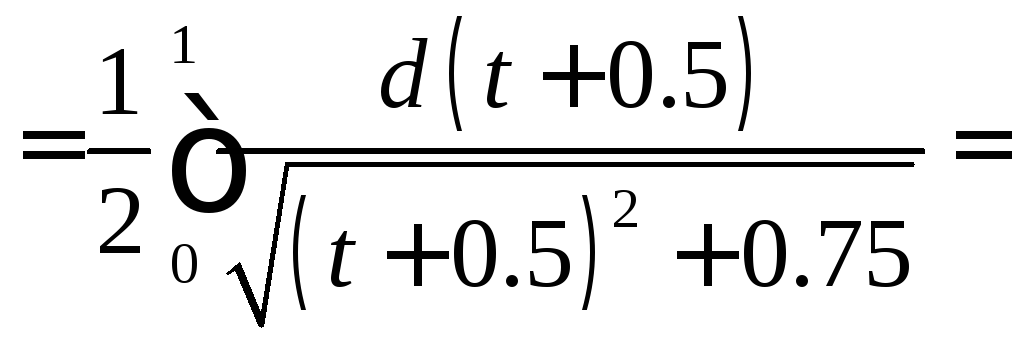
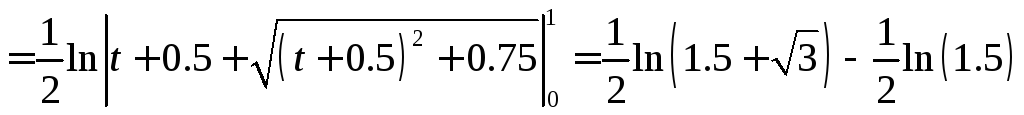
Задача №4:

Вычислить интеграл: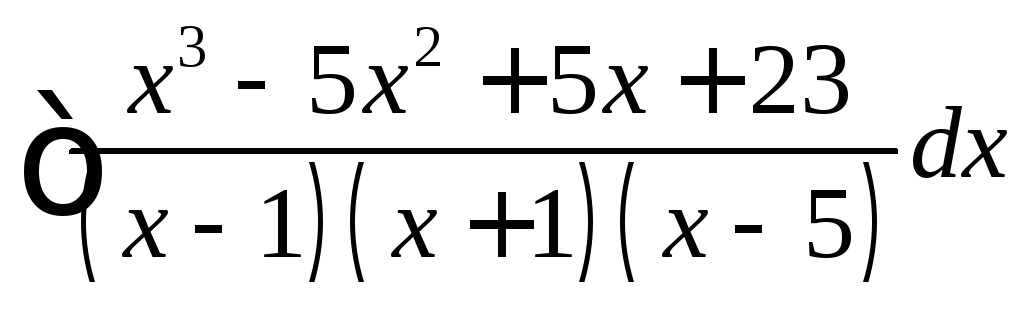

Решение:

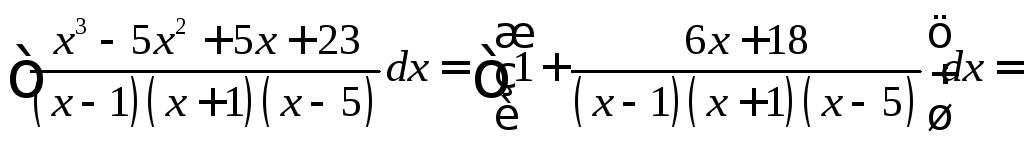
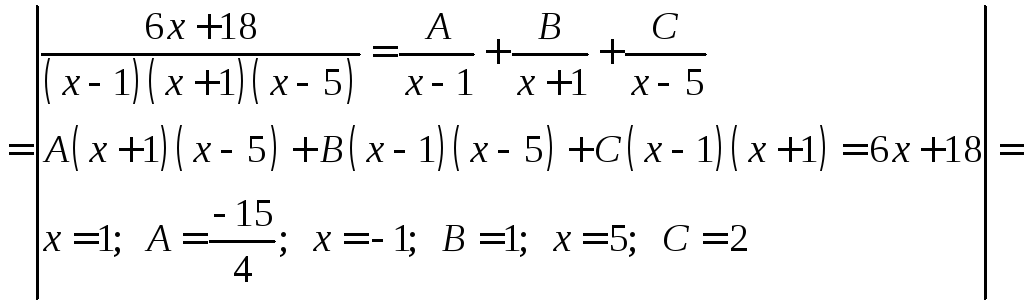
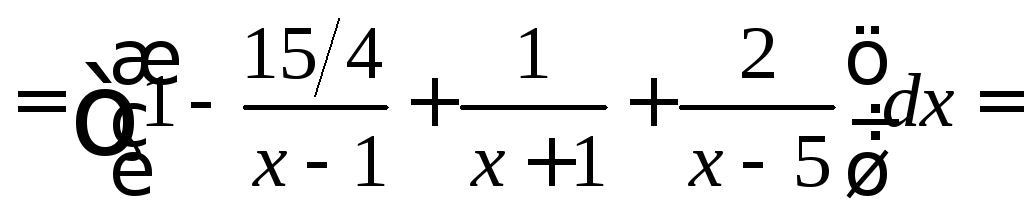
Задача №5:

Вычислить интеграл: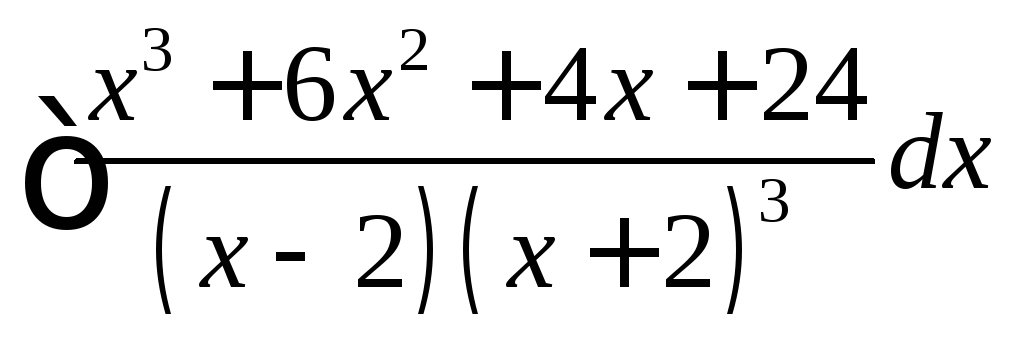

Решение:

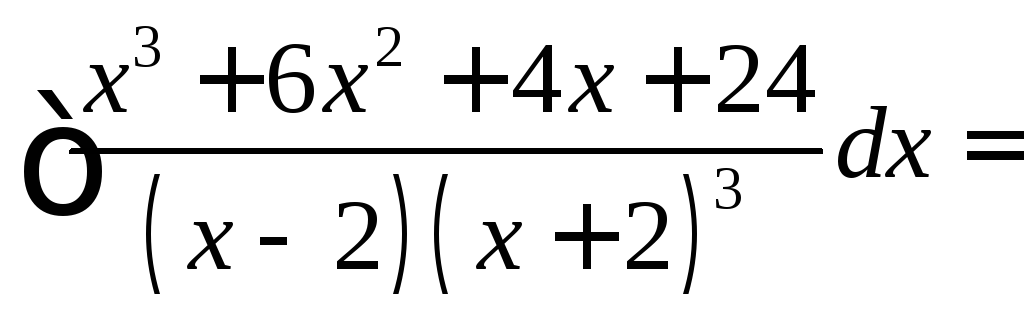
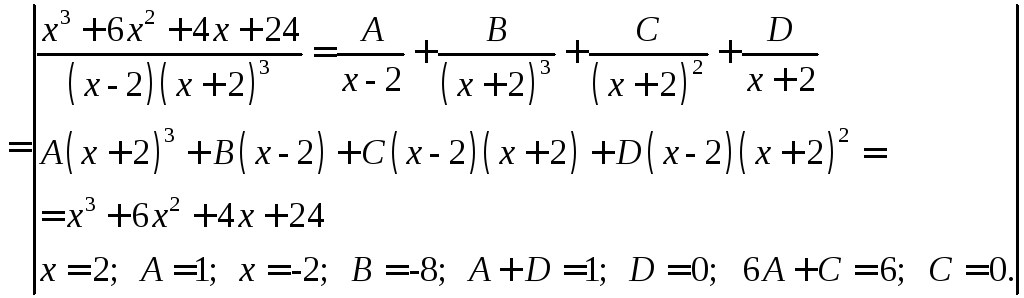
Задача №6:

Вычислить интеграл: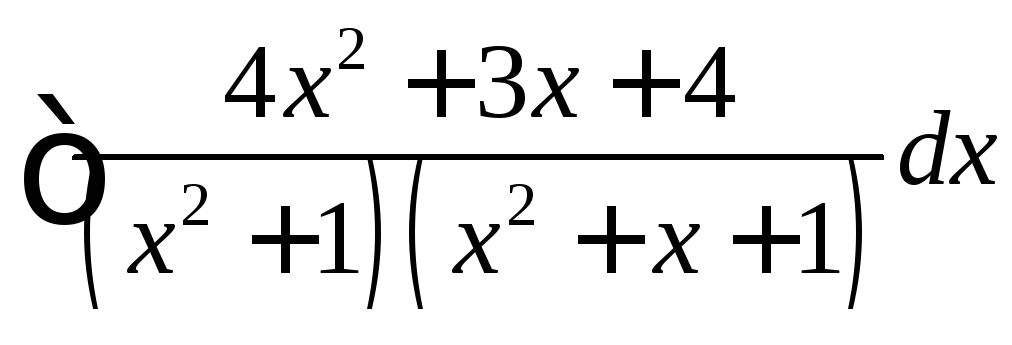

Решение:

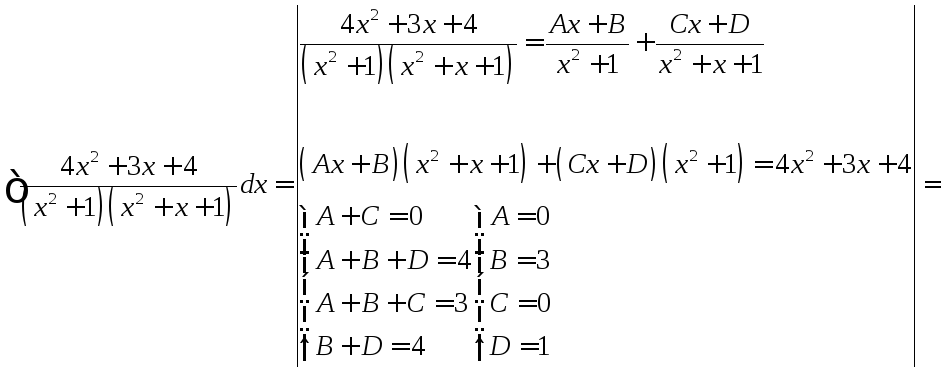
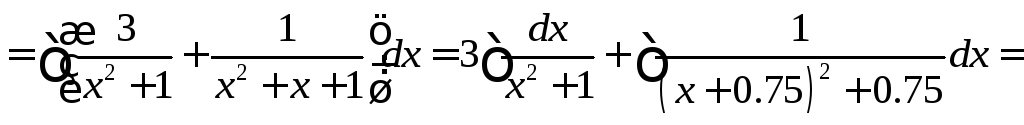
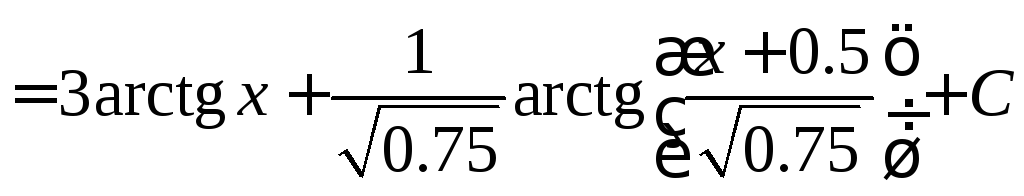
Задача №7:

Вычислить интеграл: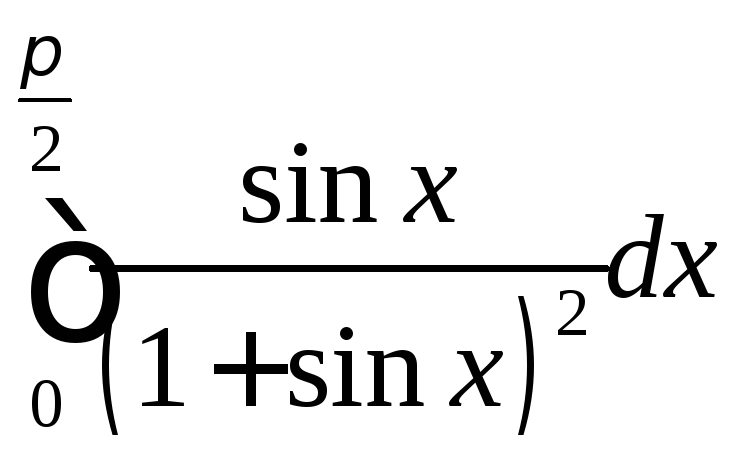

Решение:

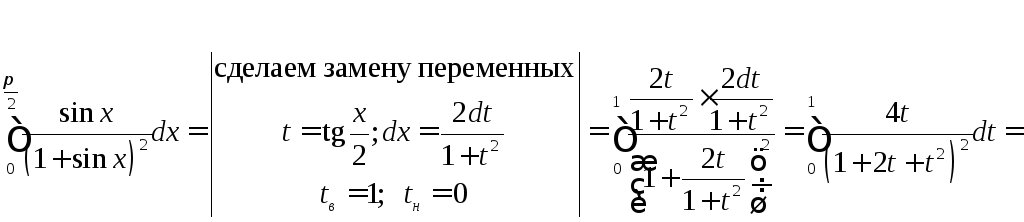
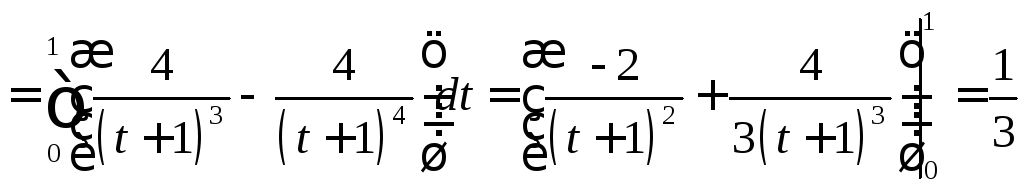
Задача №8:

Вычислить интеграл: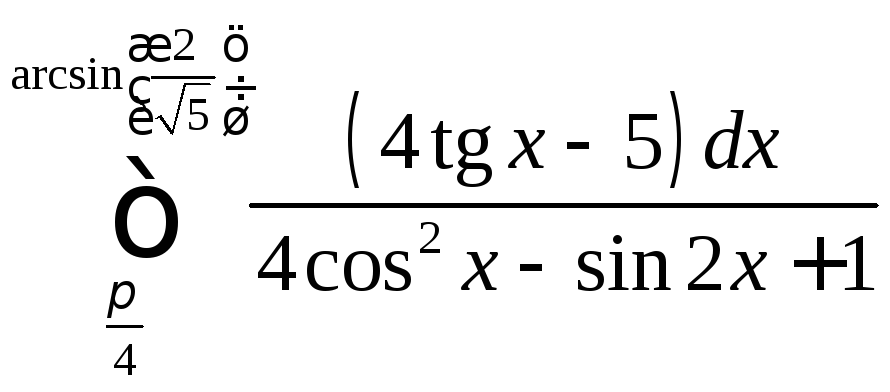

Решение:

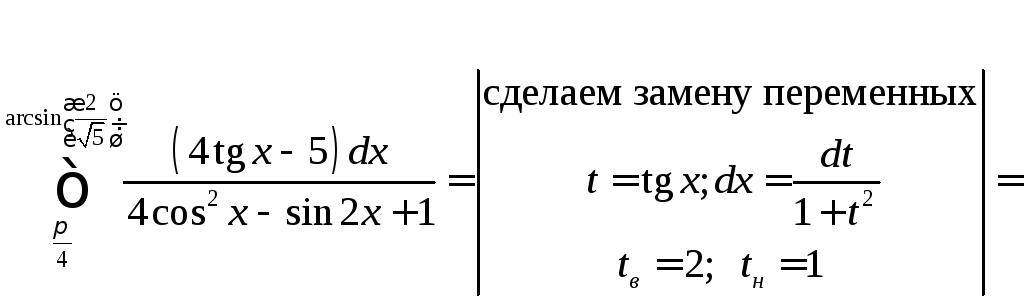
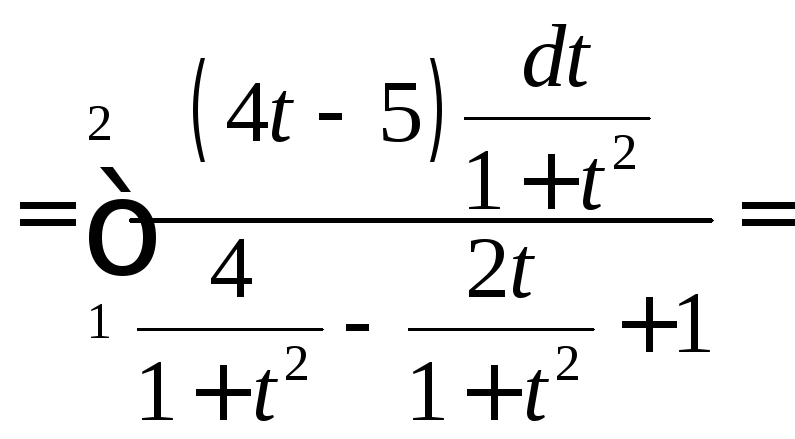
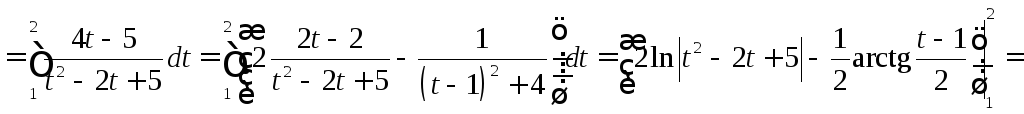
Задача №9:

Вычислить интеграл: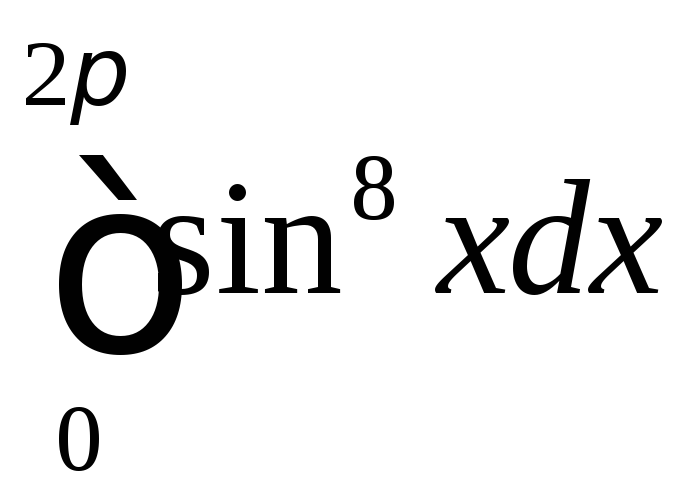

Решение:

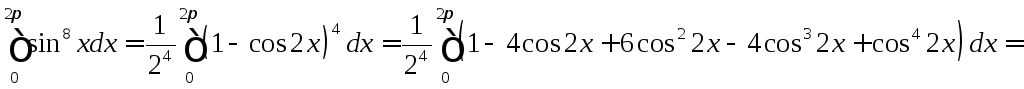
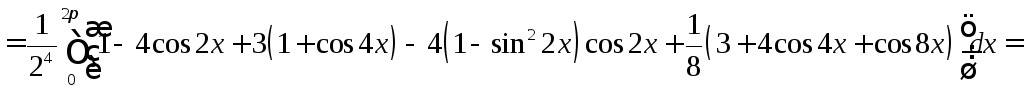
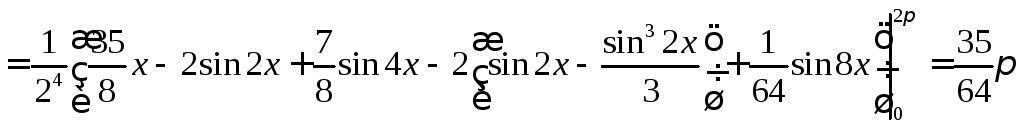
Задача №10:

Вычислить интеграл: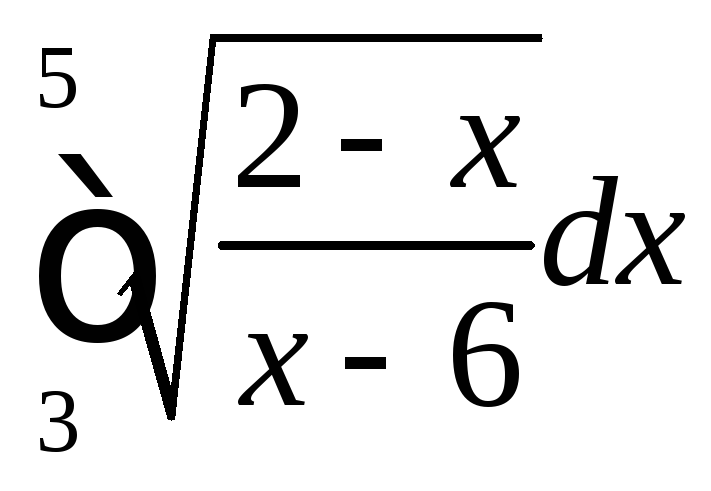

Решение:

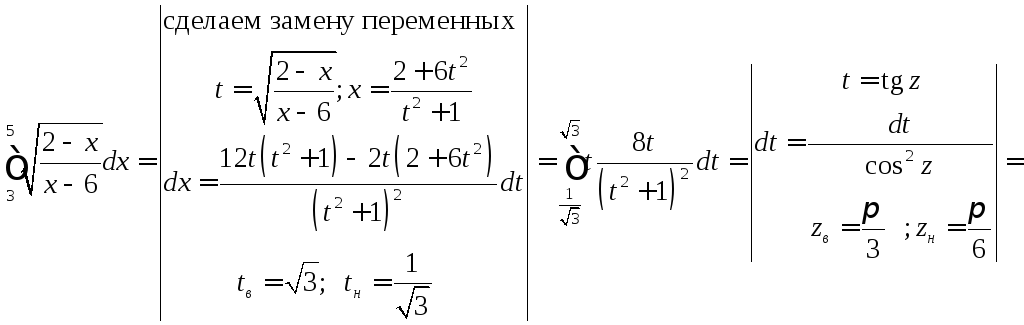
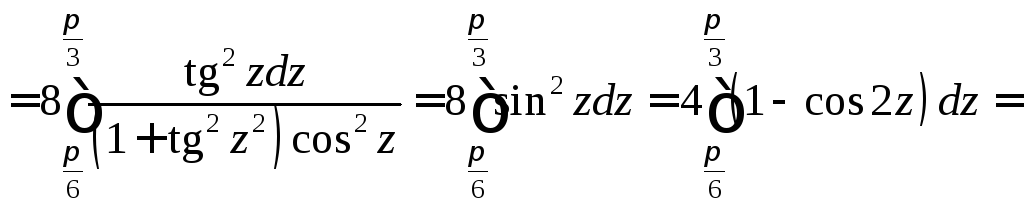
Задача №11:

Вычислить интеграл: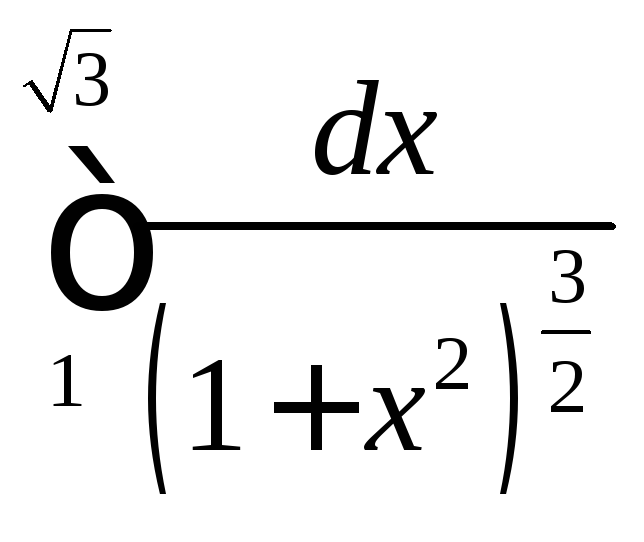

Решение:

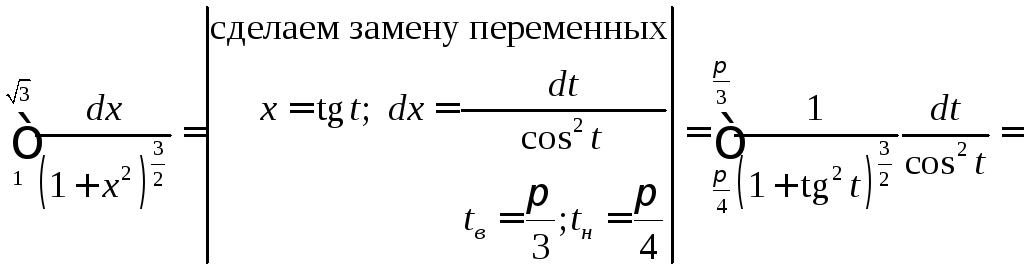
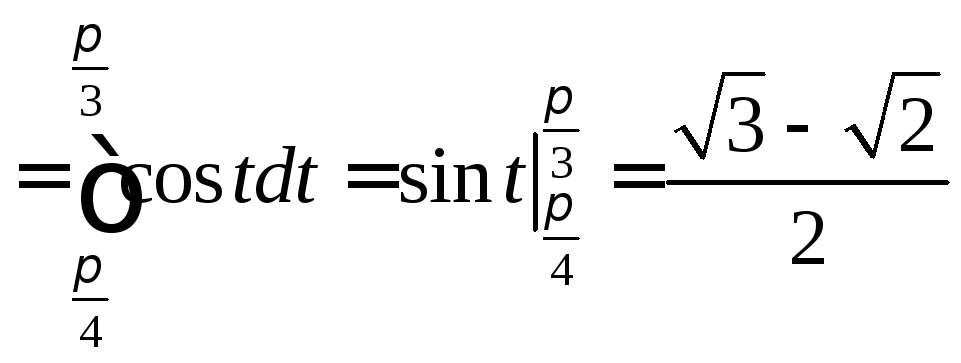
Задача №12:

Вычислить интеграл: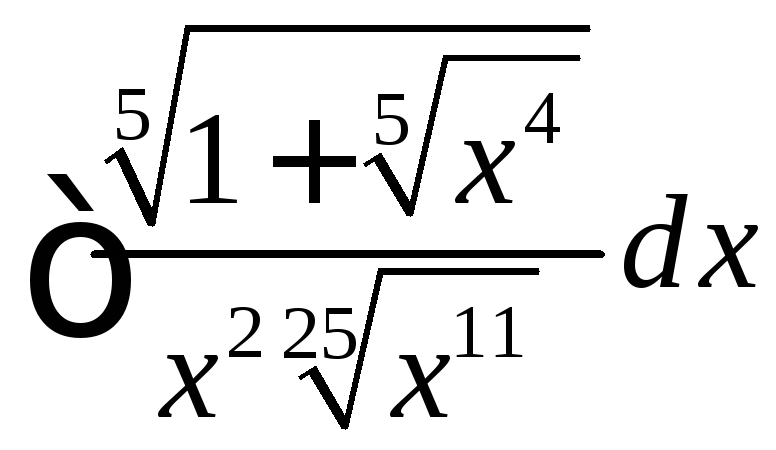

Решение:

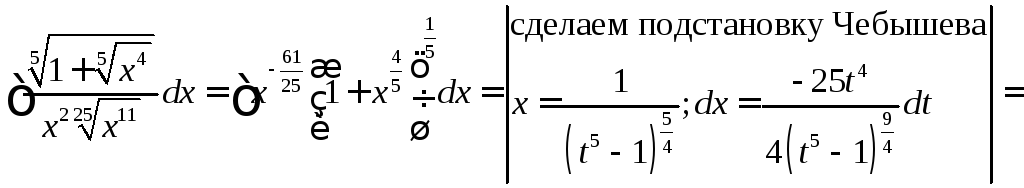
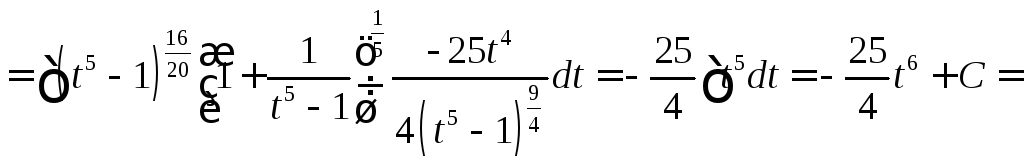
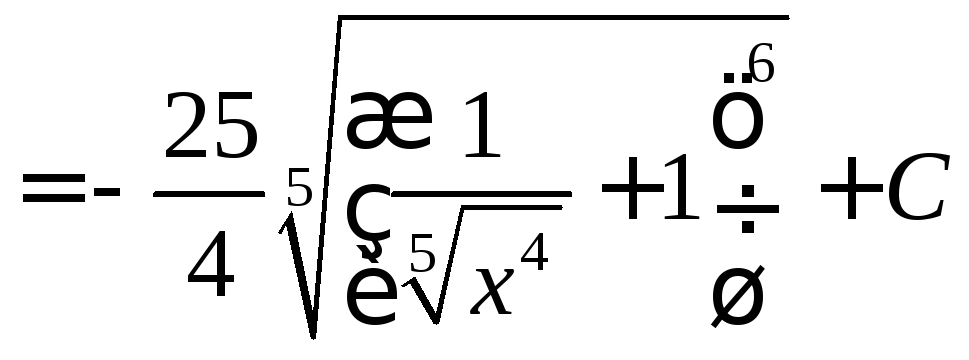
1. Функции многих переменных

Частные производные. Геометрическая интерпретация частной производной.

Пусть функция определена в некоторой окрестности точки. Функцияназываетсядифференцируемой по , если существует предел разностного отношения

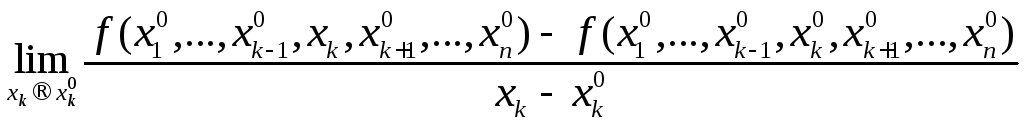(5.1)

этот предел называется частной производной функции (по) в точкеи обозначается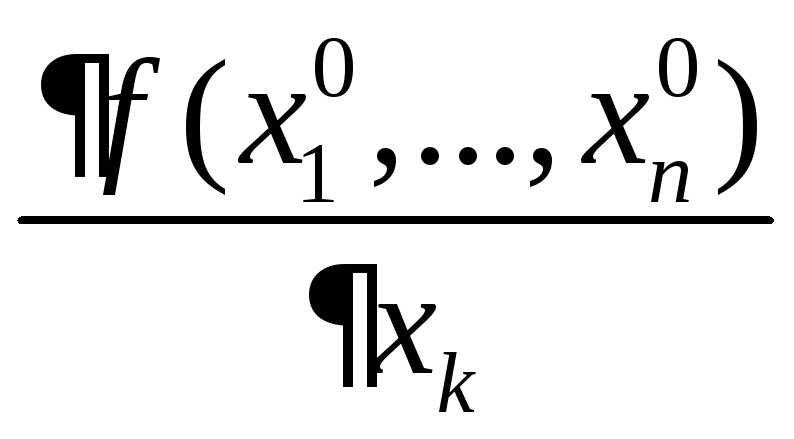или.

Таким образом, частная производная функцииравна обыкновенной производной функции действительного переменного, которая получается из, если переменныедляположить равными.

Для нахождения производной более высоких порядков, например порядка , применяется специальная формула (5.2). Эта формула получается в результате индукции при рассмотрении частных производных более низкого порядка.

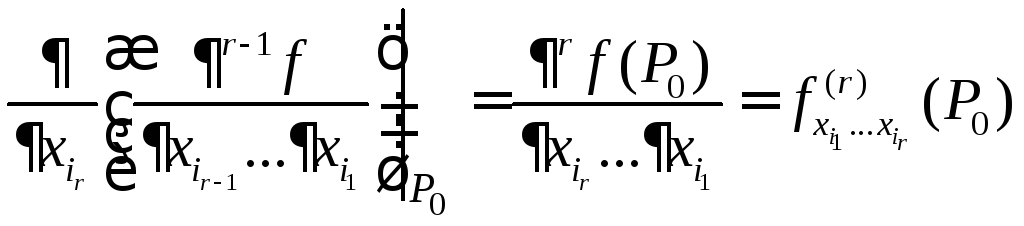(5.2).

Рассмотрим геометрический смысл частной производной на примере функции , которая дифференцируема по каждой из переменных в точке. По определениюесть число, равное, где- угол между касательной к кривой пересечения плоскости П и графика функциии плоскостью(см. рисунок ____ ). Аналогично и с.

Полный дифференциал. Производная по направлению и градиент.

Пусть область определения функциисодержит окрестность точки,. Функцияназываетсядифференцируемой в точке , если для любыхиз этой окрестности

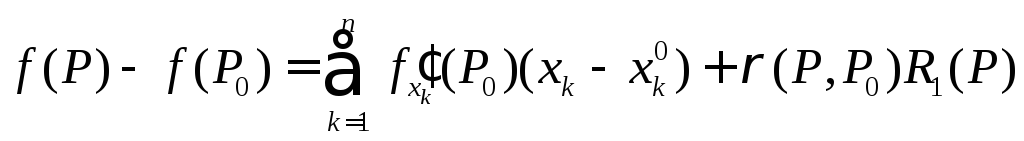(5.3),

где 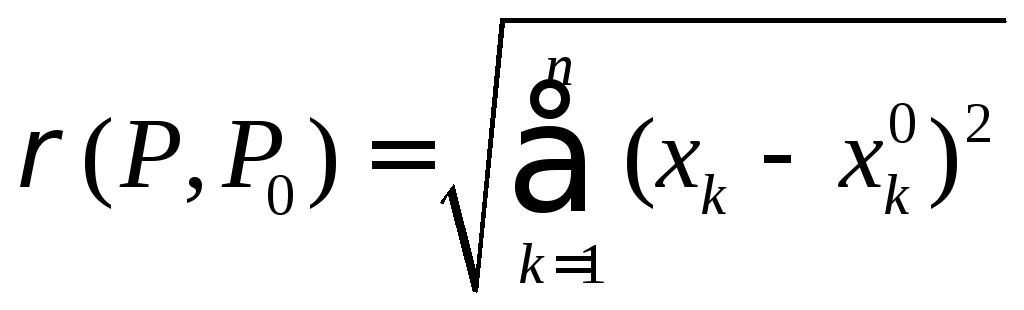и.

Линейная часть 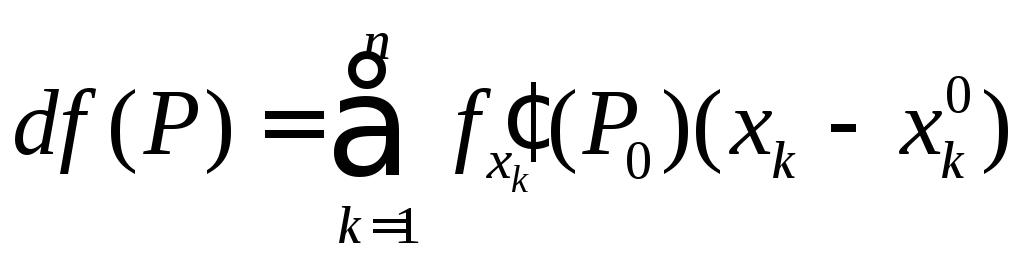приращенияназывается полным дифференциалом функциив точке.

График функции , определяемой равенством (5.4),называется касательной плоскостью к графику функциив точке.

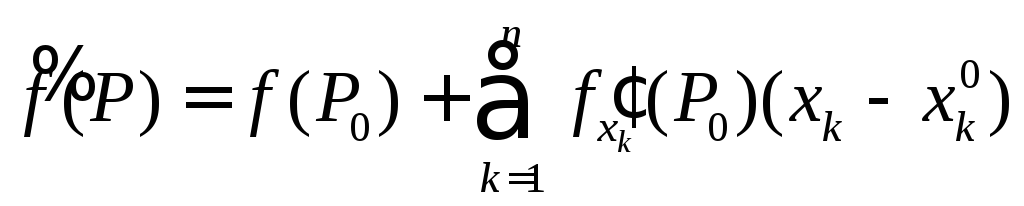(5.4)

Если дифференцируема в точке, тонепрерывна ви дифференцируема по каждому из переменных. Однако если функция непрерывна и дифференцируема по каждому из переменныхв точке, то она не обязательно дифференцируема в этой точке. Если женепрерывно дифференцируема в точке, тодифференцируема в точке.

Если дифференцируема в точке, то существует производная по направлению функциивотносительно произвольного единичного вектора , которая вычисляется по следующей формуле:

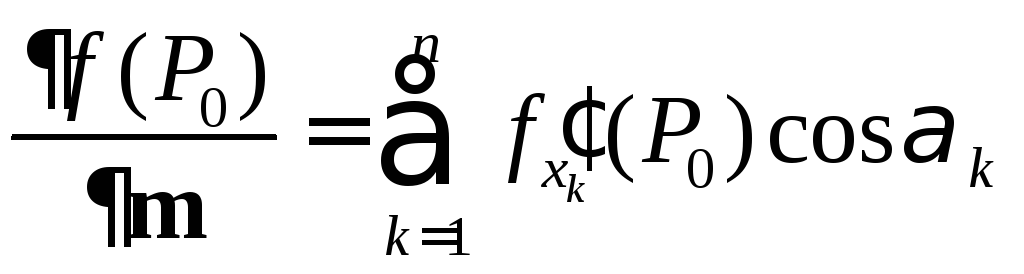(5.5),

где - угол между вектороми положительным направлением осей координат.

Если же дифференцируема по каждой из координат в точке, то векторназывается градиентом функциив точкеи обозначается символом.

Если дифференцируема в точке, то в общем случае

(5.6),

где справа стоит скалярное произведение. Если при этом - вектор в касательной плоскости к поверхности уровня, то

(5.6*)

Свойства градиента:

1. Градиент функции перпендикулярен поверхности уровня .

2. Направление градиента есть направление наиболее быстрого роста функции (т.е. направление наибольшей производной по направлению).

Теоремы о дифференцируемых ФМП.

Дифференцирование сложной функции.

Пусть дифференцируема в точкеи пусть– функции одного переменного, дифференцируемые в точкеи такие, что,. Тогда сложная функция, составленная изидифференцируема в точкеи её производная находится по формуле

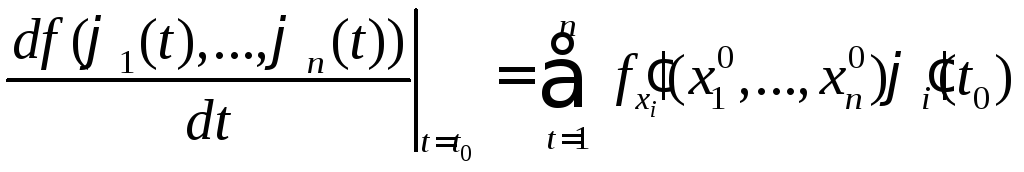(5.7)

Дифференцирование неявных функций.

Если непрерывно дифференцируема в областии существует функция, определенная ви такая, что для всехуравнениевыполняется. А кроме этого, тодифференцируема ви для каждогосправедливо равенство

или 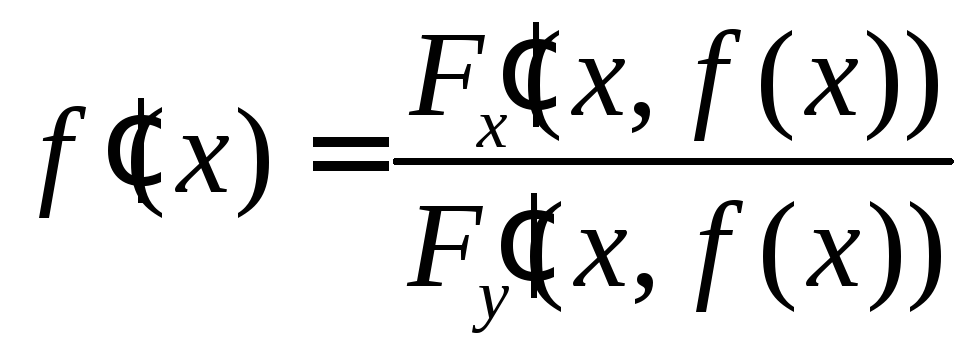(5.8).

Формула Тейлора функции двух переменных.

Пусть функция на множестве

раз дифференцируема. Тогда для всех справедлива формула

(5.9)

При этом

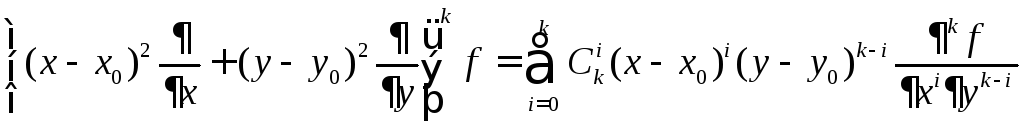
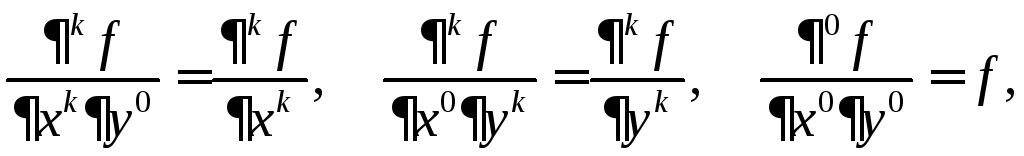
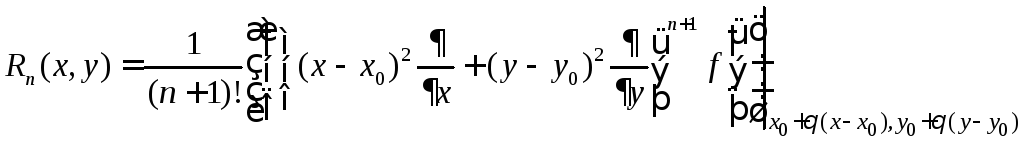(5.10)

где . Величинаназываетсяостаточным членом (в форме Лагранжа) формулы Тейлора для функции .

Если при имеет место равенство, то можно использовать формулу Тейлора для того, чтобы в некоторой окрестности точкиприблизить функцию многочленом-й степени. Формула Тейлора легко может быть обобщена на функции более чем двух переменных.

Если дифференцируема в областии для всехвыполнены соотношения, то- постоянна.

Экстремумы ФМП.

Пусть функция определена в некоторой областии- точка в. Значение функциив данной точке называетсяминимумом (локальным минимумом) функции в, если существует окрестность точкиточки, такая что для всех точек\выполняется неравенство. Аналогичномаксимумом (локальным максимумом) функции в, если. Если неравенства строгие, то локальным максимумом (минимум) называютстрогим, в противном случае – нестрогим. Максимум или минимум также называют экстремумом ( локальным экстремумом) функции в.

Необходимые условия существования экстремума.

Если - экстремум функции, дифференцируемой по каждой из координатв некоторой окрестноститочки, то выполняются равенства.

Достаточные условия существования экстремума.

Пусть функция дважды непрерывно дифференцируема ви в точкевыполняются равенства. Если, кроме того, положительно (или отрицательно) определена квадратичная форма

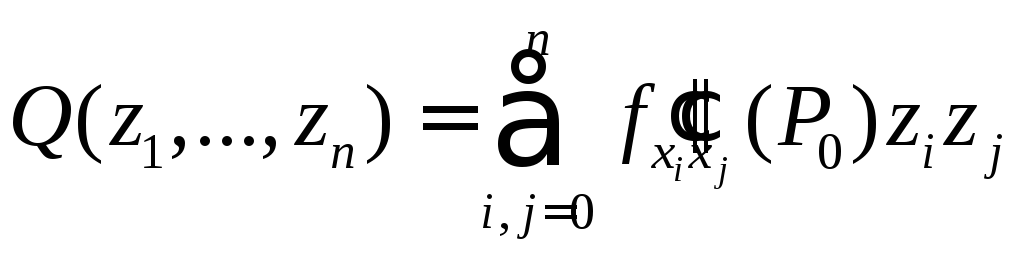(5.11)

то функция имеет минимум (или максимум) в точке, а если форманеопределенная, то функцияне имеет экстремума в точкеи точка в этом случае называетсяседловой точкой функции .

Нахождение условных экстремумов (метод неопределенных множителей Лагранжа).

Общая постановка задачи:

Найти все экстремумы и наибольшее, а также наименьшее значения функции , определенной в области, для точек, удовлетворяющихдополнительным условиям:

(5.12)

где - действительные функции, определенные в .

Необходимые условия существования условного экстремума.

Пусть функции непрерывно дифференцируемы ви ранг функциональной матрицы равен . Положим, что

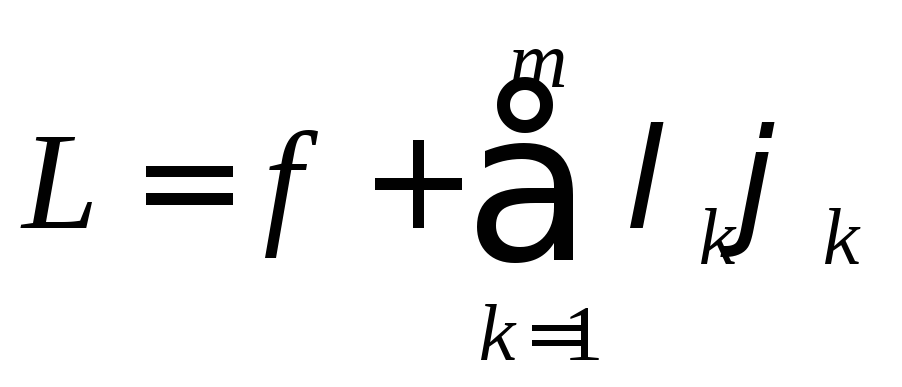(5.13)

(функция является функцией Лагранжа с множителями- произвольные действительные числа). Еслив точкепри дополнительных условиях (5.14) имеет экстремум, то справедливы соотношения:

а) 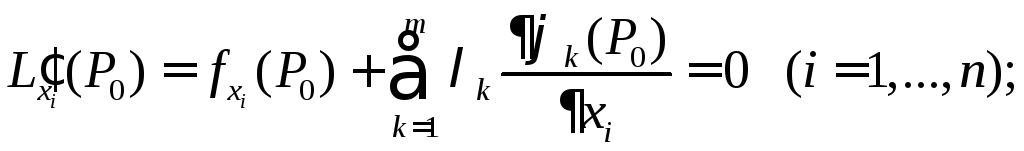_(5.14)

б)

Таким образом, необходимым условием существования условного экстремума функции в точкепри дополнительных условияхявляются следующиеуравнений сколичеством переменныхи:

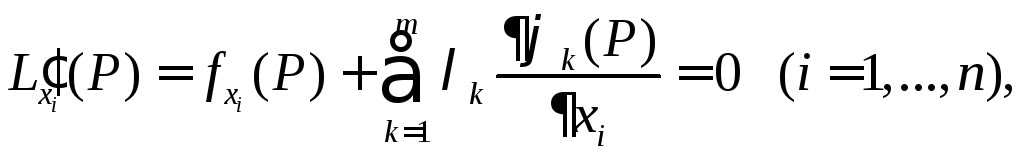_(5.15)