
Математика_Семестр1_РГР_Линал_1-3
.pdf
Расчетно-графическая работа |
313 |
Параметрические уравнения:
x 1 2t, |
|
|
t R, |
y 1 t, |
|
|
|
z 2 5t, |
|
Каноническое уравнение:
x 1 y 1 z 2 .
2 |
1 |
5 |
Уравнение прямой, определяемой как линии пересечения двух непараллельных плоскостей. Прямая l1 лежит на пересечении плоскости 1 и 2 , содержащей точки A, D, B . Уравнение 2 по-
лучим из условия компланарности векторов AM, AB, AD
|
|
|
|
|
|
|
|
x 1 |
y 1 |
z 2 |
|
|
AM |
, |
AB |
, |
AD |
2 |
1 |
5 |
0 |
||||
|
|
|
|
|
|
|
|
|
0 |
2 |
6 |
|
или 2 |
: x 3y z 4 0, следовательно, координаты точек пря- |
|||||||||||
мой l1 |
удовлетворяют системе уравнений |
|||||||||||
5x 5y z 8 0, |
1 ABC , |
|
|
|||||||||
|
|
|
|
|
|
2 |
ABD . |
|
|
|||
x 3y z 4 0, |
|
|
||||||||||
Можно сделать проверку. Непосредственная подстановка координат точки A1, 1, 2 в уравнения системы дает два тождества
1 3 1 2 4 0,
5 1 5 1 2 8 0,
и, значит, точка A принадлежит прямой l1 .
314 |
|
|
|
|
|
|
|
|
|
|
Расчетно-графическая работа |
|
||||||||||||
|
|
|
|
Направляющий вектор прямой l1 , можно найти как вектор- |
||||||||||||||||||||
ное произведение векторов нормали |
|
и |
|
плоскостей 1 |
и 2 |
|||||||||||||||||||
n1 |
n2 |
|||||||||||||||||||||||
соответственно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 n1 |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
||||||||
|
|
, |
|
5 |
5 |
1 |
|
|
. |
|
|
|
|
|
||||||||||
|
|
n2 |
|
|||||||||||||||||||||
|
|
8i 4j 20k |
|
|
|
|
|
|||||||||||||||||
q |
|
|||||||||||||||||||||||
|
|
1 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Поскольку |
q |
2 |
8, 4,20 4 2, 1,5 , то векторы |
q |
1 и |
q |
2 |
колли- |
||||||||||||||||
неарны и оба могут служить направляющими векторами нашей пря-
мой.
2.3. Найдем площадь ABC . Поскольку
AB,AC 20,20, 4 ,
то
S ABC |
|
1 |
|
|
AB |
, |
|
|
|
|
1 |
|
|
2 |
|
. |
|
|
|
AC |
|
|
816 |
51 |
|||||||||||
|
|
||||||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||
Сначала составим уравнение высоты ABC, опущенной на сторону
AB , и найдем ее длину.
2.4. Пусть CE искомая высота и E x1,y1,z1 . Точка E принадле-
жит прямой l1 , поэтому существует такое t t1 , что (параметриче-
ские уравнения)
x1 1 2t1,
y1 1 t1,z1 2 5t1.
С другой стороны, т.к. CE AB , имеем (CE, AB) 0 или
Расчетно-графическая работа |
315 |
2 x1 3 1 y1 2 5 z1 3 0,
Следовательно,
21 2t |
3 1 1 t |
2 5 2 5t |
3 0, откуда t |
|
|
|
3 |
и, |
||||||||||||||||||||||||||
|
|
5 |
||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||
x |
1 |
, |
y |
8 |
, |
z 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
8 |
|
|
|
|
|
|
16 |
18 |
10 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Таким образом, E |
|
|
, |
|
,1 , |
CE |
|
|
, |
|
, |
|
|
|
|
|
|||||||||||||||||
|
5 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
5 |
5 |
|
5 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
162 182 |
102 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
и |
|
|
h |
CE |
|
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
25 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1
2-ой способ. Поскольку известно, что S ABC 2 h AB , а
S ABC 2
 51, AB
51, AB 
 30 , то.
30 , то.
h 2S ABC 4 51 2 34 ,
AB 30 5
что совпадает с ранее полученным результатом.
Уравнение высоты составим, выбрав в качестве направляю-
щего вектора q3 5CE 8,9,5 и в качестве начальной точки —
2
точку C 3,2,3 . Параметрическое уравнение высоты имеет следую-
|
x 8t 3, |
|
щий вид |
|
t R . |
y 9t 2, |
||
|
|
|
|
z 5t 3, |
|
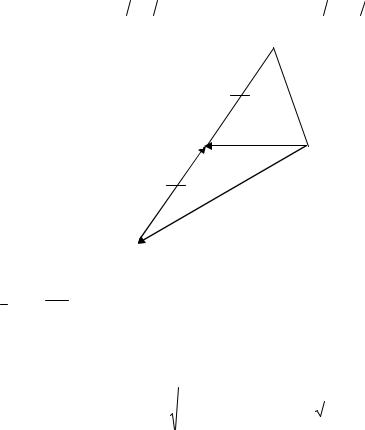
2.5. Рассмотрим медиану CM в ABC (рис.6.10).
316 |
|
|
|
|
|
|
|
|
Расчетно-графическая работа |
|
||||||||
Очевидно, что |
|
|
|
|
|
, где |
|
|
2, 3, 5 , |
|
||||||||
CM |
CA |
AM |
CA |
|
||||||||||||||
|
|
|
1 |
|
|
1, 1 |
2,5 2 , поэтому |
|
3, 7 |
2, 5 2 . |
||||||||
|
AM |
|
AB |
CM |
||||||||||||||
|
|
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M
C
A
Рис. 6.10
Параметрическое уравнение медианы (направляющий вектор q4 2СM 6,7,5 , начальная точка C 3,2,3 )
|
|
|
x 6t 3, |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
t R . |
|
|
|
|
|||
|
|
|
y 7t 2, |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 5t 3, |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
7 |
2 |
|
5 |
2 |
|
1 |
|
|
|
||
Длина медианы m |
CM |
|
|
|
|
110 . |
||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
||||||||||
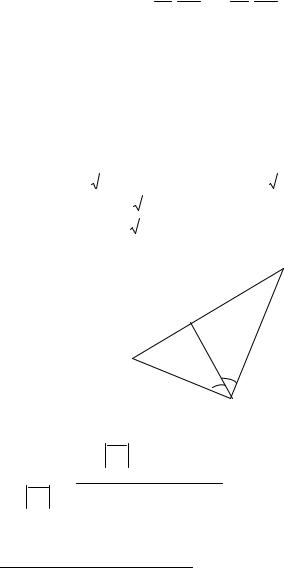
2.6. Рассмотрим биссектрису CK угла ACB , найдем ее длину и составим уравнение биссектрисы.
1-ый способ. Воспользуемся параметрическим уравнением прямой l1 , которому удовлетворяют координаты точки K x2 ,y2 ,z2 при
|
x2 2t2 1, |
|
некотором значении t2 параметра |
|
t2 1, |
y2 |
||
|
|
5t2 2. |
|
z2 |
|
Расчетно-графическая работа |
317 |
Поскольку CK − биссектриса, то углы и cos cos . Поэтому
|
|
|
|
|
|
cos |
|
(CA,CK ) |
|
|
(CB,CK ) |
cos . |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CA |
|
|
CK |
|
|
|
|
|
|
CB |
|
|
|
CK |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, получим |
( |
|
|
|
|
, |
|
|
|
) |
|
( |
|
|
|
|
, |
|
|
|
|
) |
или, учи- |
||||||||||||||||||||||||
Сокращая здесь на |
|
|
|
|
|
|
|
CA |
CK |
CB |
CK |
|||||||||||||||||||||||||||||||||||||||||||||||||
CK |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CA |
|
|
|
|
|
|
|
|
|
|
CB |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
тывая, что |
|
|
2 2t2 , 3 t2 , 5 5t2 , |
|
|
4, 4,0 , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
CK |
CB |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2, 3, 5 , придем к равенству |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
CA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
2 2 2t2 3 3 t2 |
5 5 5t2 |
|
4 2 2t2 4 3 t2 |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
38 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
откуда t2 |
76 10 |
|
|
|
|
|
0,522. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
36 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Таким образом, CK 3,04; 3,52; 2,4 и длина биссектрисы
b CK 
 3,04 2 3,52 2 2,4 2 5,23.
3,04 2 3,52 2 2,4 2 5,23.
2 Расчеты проводим с точностью до второго знака после запятой.

318 Расчетно-графическая работа
Уравнение биссектрисы (направляющий вектор q5 CK , начальная
|
x 3 t 3,04, |
|
точка C 3,2,3 ) имеет вид |
|
t R . |
y 2 t 3,52, |
||
|
|
|
|
z 3 t 2,4, |
|
2-ой способ. Из элементарной геометрии известно, что точка K (ос-
нование биссектрисы) делит основание AB в отношении |
|
, где |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AK |
|
AC |
|
|
|
|
|
|
|
|
1,09. |
|
|
|
|
|
|
|
38 |
|
|
|
19 |
|
|
|
||||
|
|
|
|
|
|
|
4 |
|
|
|
||||||
|
KB CB |
32 |
|
|
|
|
|
|
||||||||
При этом координаты точки K x2 , y2,z2 вычисляются через коор-
динаты концов отрезка AB по известным формулам деления отрезка в заданном отношении (формулы 3.2). Подставляя в эти формулы соответствующие значения координат, получим
x2 |
|
1 1,09 1 |
|
0,04; |
y2 |
|
1 1,09 2 |
1,52; |
|||
|
|
||||||||||
|
1 |
1,09 |
|
|
|
|
|
1 1,09 |
|||
z2 |
|
2 |
1,09 |
3 |
0,61. |
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
1 1,09 |
|
|
|
|
|
|
|
|
откуда CK 3,04; 3,52; 2,39 . Длина биссектрисы
b CK 
 3,04 2 3,52 2 2,39 2 5,23, что совпадает с преды-
3,04 2 3,52 2 2,39 2 5,23, что совпадает с преды-
дущими вычислениями.
3. Рассмотрим теперь пирамиду DABC :
3.1. Составим уравнение высоты, опущенной из вершины D на основание, и найдем ее длину.
1-ый способ. Высоту пирамиды найдем, подставив координаты точ-
ки D 1, 3,4 в нормированное уравнение плоскости 1

|
|
|
|
|
|
Расчетно-графическая работа |
319 |
||||||
H d |
|
1 |
|
|
|
5 1 5 3 4 8 |
|
|
16 |
|
. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
51 |
|
|
|
|
51 |
|
|
||||||
|
|
|
|||||||||||
2-ой способ. Найдем сначала координаты точки Q x3, y3,z3 – про-
екции вершины D на плоскость основания 1 .. Очевидно, числа x3 ,y3 ,z3 удовлетворяют общему уравнению плоскости 1
5x3 5y3 z3 8 0 ,
но одного этого уравнения недостаточно для определения трех неиз-
вестных чисел. В то же время легко заметить, что вектор
DQ x3 1, y3 3,z3 4 коллинеарен вектору нормали
N 5,5, 1 плоскости 1 , т.е. DQ N , где 0 некоторая постоянная. Последнее равенство равносильно трем соотношениям
x3 1 5 , y3 3 5 , z3 4 .
Воспользовавшись этими соотношениями, получим
51 5 5 3 5 4 8 0,
откуда 16 , и в результате
51
DQ N 16 5,5, 1 .
51 |
16 |
|
|
|
|
16 |
|
|
||
|
|
|
|
|
|
, что подтверждает |
||||
Высота пирамиды H |
|
52 52 |
12 |
|||||||
|
|
|
|
|||||||
51 |
|
|
51 |
|
||||||
предыдущие вычисления.
3.2. Найдем теперь объем пирамиды DABC .
1-ый способ.
Vпир |
|
1 |
HS |
|
|
1 |
16 |
|
|
|
|
32 |
. |
||
ABC |
|
|
204 |
||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
51 |
|||||||||||||
|
3 |
|
|
3 |
3 |
|
|||||||||

320 Расчетно-графическая работа
2-ой способ. Вычислим теперь объем пирамиды через смешанное произведение векторов AB, AC,AD
Vпир |
1 |
|
| |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
, |
|
|
| |
1 |
|
|
64 |
|
|
|
32 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||
AB |
|
AC |
AD |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3.3. Угол между гранями пирамиды ABC и ADB это угол между |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
плоскостями 1 |
и 2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
cos |
|( |
|
|
|
, |
|
|
|
|
|
|
|
|
)| |
|
|
| 5 1 |
|
5 3 |
1 1| |
|
|
|
9 |
|
0,38, |
|
|||||||||||||||||||||||||||||
n1 |
n2 |
|
|
68 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n1 |
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
51 11 |
561 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
3.4. Угол между ребром пирамиды DA и ее основанием найдем, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
используя скалярное произведение векторов |
|
|
|
(0,2, 6) и |
||||||||||||||||||||||||||||||||||||||||||||||||||||
DA |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
5,5, 1 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
n1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
cos |
|( |
|
, |
|
|
|
|
|
)| |
|
|0 5 |
2 |
5 |
|
6 1 | |
|
|
4 |
|
|
|
|||||||||||||||||||||||||||||||||||
DA |
n1 |
0,18, 80 и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
DA |
|
|
|
n1 |
|
|
|
|
|
|
|
|
|
|
|
|
40 51 |
510 |
|
|
|
||||||||||||||||||||||||||||
900 800 100 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
4. Составим уравнение прямой lCD |
(проходит через точки C и D, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
направляющий вектор q6 CD 2, 5,1 , начальная точка
C 3,2,3 ): x 3 y 2 z 3 . Напомним каноническое уравнение
2 |
5 |
1 |
прямой lAB (проходит через точки A и B , направляющий вектор
q1 2, 1,5 ):
x 1 y 1 z 2 .
2 |
1 |
5 |

|
|
|
|
|
|
|
|
|
Расчетно-графическая работа |
321 |
||||||||
4.1. Угол между угол между прямыми lCD |
и lAB . |
|||||||||||||||||
cos |
|( |
|
|
, |
|
6 |
)| |
|
| 2 2 |
1 5 5 1| |
|
|
7 |
, откуда 62 . |
||||
q1 |
q |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
q1 |
|
q |
6 |
|
|
|
30 30 |
15 |
|
|
||||||
4.2. Расстояние между скрещивающимися прямыми.
1-ый способ. Вычислим объем параллелепипеда, построенного на
векторах |
q1 AB, |
q |
6 CD и AC. Поскольку |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
5 |
|
64, |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
, |
|
, |
|
|
2 |
5 |
1 |
|
|||
|
|
|
AB |
CD |
AC |
||||||||||
|
|
|
|
2 |
3 |
5 |
|
|
|||||||
то объем параллелепипеда Vo | AB CD AC | 64.Площадь осно-
вания параллелепипеда Sосн AB,CD . Вычислим векторное про-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
изведение |
|
|
|
|
i |
|
j |
k |
|
|
|
|
|
|
|
|
||||
AB |
, |
CD |
2 |
1 |
5 |
|
24i |
8j 8k , |
||||||||||||
|
|
|
|
|
2 |
5 |
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и, следовательно, Sосн AB,CD .
В результате расстояние между скрещивающимися прямыми равно
d H |
V0 |
|
64 |
|
|
|
8 |
|
. |
|
Sосн |
|
|
|
|
|
|
||||
8 11 |
11 |
|
||||||||
|
|
|||||||||

322 Расчетно-графическая работа
2-ой способ. Через прямую l1 проведем плоскость 0 , которая будет
параллельна прямой l6 . Эта плоскость содержит точку A 1, 1,2 и
имеет направляющие векторы q1 AB 2, 1,5 ,
q6 CD 2, 5,1 . Запишем общее уравнение этой плоскости:
x 1 |
y 1 |
z 2 |
|
2 |
1 |
5 |
24(x 1) 8(y 1) 8(z 2) 24x 8y 8z 16 0 |
2 |
5 |
1 |
|
После умножения на нормирующий множитель
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
8 |
32 1 1 |
8 |
11 |
|||||
получим нормированное уравнение 0
1 3x y z 2 0. 
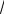 11
11
Расстояние между скрещивающимися прямыми найдем как расстоя-
ние от точки C 3,2,3 прямой l6 |
до плоскости 0 : |
|||||||||||
d |
|
1 |
|
|
3 3 2 3 2 |
|
|
|
8 |
|
, |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||
11 |
|
|
|
|
11 |
|
||||||
|
|
|
||||||||||
что подтверждает полученный выше результат.
