
Математика_Семестр1_РГР_Линал_1-3
.pdf
Расчетно-графическая работа |
303 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1 |
|||
|
|
|
2 |
|
|
|
|
|
||||
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
M0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
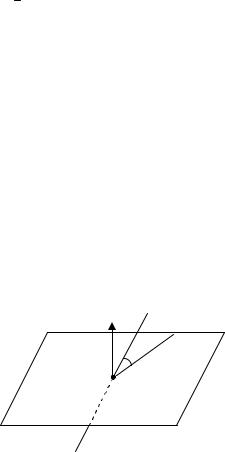
Рис. 6.6
Поэтому в качестве направляющего вектора прямой можно выбрать вектор
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
i |
|
j |
k |
|
|
|
|
|
|
9,6,9 |
|||||
|
S |
N |
1, |
N |
1 |
3 |
1 |
9i |
6 |
j |
9k |
|||||||||||
|
2 |
3 |
4 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или вектор s0 S3 3,2,3 , коллинеарный вектору S .
Для составления уравнения прямой необходимо также найти координаты любой точки M0 x0 , y0 ,z0 , принадлежащей прямой l .
Эти координаты находят как одно из решений системы1:
x 3y z 5 0,
|
|
|
|
|
|
(6.3) |
|
|
|
2x 3y 4z 1 0. |
|
||
Полагая, например, в (6.3) z 0, получим: |
|
|||||
x |
0 |
3y |
0 |
5, |
y0 1, |
|
|
|
|
x0 2, |
|||
2x0 |
3y0 1. |
|
||||
1 Система имеет бесконечно много решений, ей удовлетворяют координаты каждой точки прямой.
304 |
Расчетно-графическая работа |
и точка M0 имеет координаты M0 2, 1,0 .
Канонические уравнения прямой, проходящей через точку M0 па-
раллельно вектору |
s |
0 |
, имеют вид: |
x 2 |
|
y 1 |
|
z |
. |
|
|
|
|||||||
|
|
|
3 |
2 |
3 |
|
|||
Задача 7. Найти точку пересечения прямой l и плоскости , а так-
же угол между прямой l и плоскостью . Данные по прямой l и
плоскости взять из предыдущих пунктов 3 и 6.
Решение. В задаче 3 этого раздела получено уравнение плоскости
: |
43x 22y 17z 113 0 , |
а в задаче 6 получены канонические |
||||||||
уравнения прямой l: |
x 2 |
|
y 1 |
|
z |
. |
Перейдем к параметриче- |
|||
|
|
|
||||||||
|
3 |
|
2 |
3 |
|
|
|
|||
ским уравнениям прямой |
|
|
|
|
|
|
|
|||
|
|
|
x 3t 2, |
|
|
|||||
|
|
|
|
|
|
|
|
|
t R . |
(6.4) |
|
|
|
y 2t 1, |
|||||||
z 3t,
Точке M0 (рис.6.7) пересечения прямой и плоскости соответствует некоторое значение параметра t0 .
l
M0
Рис. 6.7
Для получения t0 подставим выражения (6.4) в уравнение плоскости:
43 3t0 2 22 2t0 1 17 3t0 113 0,
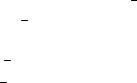
|
|
|
Расчетно-графическая работа |
305 |
||||||
|
|
|
224t |
|
49 0, t |
|
|
7 |
. |
|
|
|
|
0 |
0 |
32 |
|
||||
|
|
|
|
|
|
|
|
|||
Подставляя t0 |
в (6.4), получим координаты точки |
пересечения |
||||||||
M0 3285, |
9 |
, |
3221 . |
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|||
Угол между прямой и плоскостью (или угол между прямой и |
||||||||||
проекцией этой прямой на плоскость) |
|
|
|
|
|
|||||
найдем как угол 2 , |
||||||||||
где — угол между направляющим вектором прямой и вектором
нормали к плоскости. |
|
Направляющий вектор прямой |
s |
и вектор |
||||||||||||||||||||||||||
нормали к плоскости |
|
|
имеют вид: |
s |
|
3,2,3 и |
|
43,22,17 . |
||||||||||||||||||||||
|
N |
N |
||||||||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|( |
s |
, |
|
|
|
)| |
|
|
|
14 |
|
|
|
|
|
|||||||
|
|
|
|
cos sin |
|
|
|
|
|
, |
|
|||||||||||||||||||
|
|
|
N |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
откуда arcsin |
14 |
|
69 . |
|
|
s |
|
N |
15 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 8а. Найти точку M1 , симметричную точке M 1,0, 2 отно- |
||||||||||||||||||||||||||||||
сительно плоскости |
|
:2x y z 3 0 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Решение. |
Составим уравнение прямой l , проходящей через точку |
|||||||||||||||||||||||||||||
M перпендикулярно плоскости |
|
(рис.6.8). В качестве направ- |
||||||||||||||||||||||||||||
ляющего |
вектора |
|
|
|
|
прямой |
можно |
выбрать вектор |
нормали |
|||||||||||||||||||||
S |
|
|||||||||||||||||||||||||||||
|
|
2, 1,1 |
к плоскости. Полагая, что |
|
|
|
|
2, 1,1 , перейдем к |
||||||||||||||||||||||
|
N |
|
|
S |
N |
|||||||||||||||||||||||||
параметрическим уравнениям прямой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
x 2t 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t R . |
(6.5) |
||||||||
|
|
|
|
|
|
|
|
|
|
y t, |
|
|
|
|
|
|||||||||||||||
z t 2,
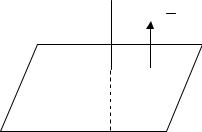
306 |
Расчетно-графическая работа |
M 
N
O 
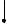 M1
M1
Рис. 6.8
Найдем координаты точки O x0 , y0 ,z0 пересечения прямой и плос-
кости, подставив выражение (6.5) в уравнение плоскости:
|
|
|
|
|
2 2t |
0 |
|
1 t |
0 |
t |
0 |
2 3 0 |
|
t |
0 |
1 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||
Точка O |
имеет координаты O |
2, |
1 |
, 3 |
. Поскольку точка O яв- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
ляется серединой отрезка MM1, то |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
xM |
xM |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x0 |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
xM1 |
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
x |
|
|
2x |
|
x |
|
|
|
2 2 1 3, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
M1 |
0 |
M |
, |
|
||||||||||||||
|
|
|
|
yM |
yM |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 1, |
|||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||||
y0 |
|
|
|
|
|
|
, |
yM1 |
2y0 |
yM , |
|
yM1 |
||||||||||||||||
|
2 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||
|
|
|
|
zM |
zM |
|
|
|
|
|
zM |
1 |
2z0 |
zM , |
|
zM |
|
2 ( |
) 2 1. |
|||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
z0 |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: точка M1 имеет координаты M1 3, 1, 1 .
Расчетно-графическая работа |
307 |
Задача 8б. Найти точку M1 , симметричную точке M 1,0, 2 отно-
сительно прямой l : |
x 2 |
|
y |
|
z 1 |
. |
|
2 |
|
||||
1 |
|
|
3 |
|||
Решение. Сначала составим уравнение плоскости , проходящей
через точку M перпендикулярно прямой l (рис. 6.9).
S l
M
O
M1
Рис. 6.9
Вектор нормали N к плоскости совпадает с направляющим век-
тором S прямой l — N S 1,2, 3 . Тогда уравнение плоско-
сти имеет вид: 1 x 1 2 y 0 3 z 2 0 или x 2y 3z 7.
Найдем координаты точки O x0 y0 ,z0 пересечения прямой l и
плоскости так, как мы это делали в задаче 7.

308 |
Расчетно-графическая работа |
Запишем параметрические уравнения прямой l :
x t 2, |
|
|
t R . |
y 2t, |
|
|
|
z 3t 1, |
|
Подставим эти выражения в уравнение плоскости и найдем соответ-
ствующее значение параметра t0 :
|
|
|
|
|
|
|
t |
0 |
|
|
2 2 2t |
0 |
3 3t |
0 |
1 7 |
t |
0 |
|
1 . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
||||
Итак, точка O имеет координаты O 157 |
, 72, 107 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
Поскольку точка O является серединой отрезка MM1 , |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
xM |
xM |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x0 |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
x |
|
|
|
30 1 |
23 |
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
xM1 2x0 xM , |
|
|
|
|
, |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
yM |
yM |
|
|
|
|
|
|
|
M1 |
|
7 |
|
7 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 , |
|
|
|
||||||
y0 |
|
|
|
|
|
|
|
1 |
, |
yM |
2y0 yM , |
yM |
|
|
|
0 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
7 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
20 |
|
7 |
|
6 |
|
|||
|
|
|
|
z |
|
z |
|
|
|
|
|
|
|
|
zM |
|
2z0 zM , |
|
z |
|
|
|
2 |
. |
||||||||||
|
|
|
M |
M1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
7 |
7 |
||||||||||||||
z |
0 |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: точка M1 имеет координаты M1 237 , 74, 67 .
Расчетно-графическая работа |
309 |
6.4.Приложение векторной алгебры
ианалитической геометрии.
Расчет пирамиды
●Условия задач
1. Выбрать в декартовой прямоугольной системе координат четыре произвольные точки A,B,C,D так, чтобы они не лежали ни в одной из координатных плоскостей.
1.1.Проверить, не принадлежат ли эти точки одной плоскости (ес-
ли все они расположены в одной плоскости, то следует изме-
нить координаты одной из точек).
1.2.Проверить, не является ли треугольник ABC равнобедрен-
ным (в случае утвердительного ответа измените координаты
одной из точек).
2.Рассмотреть пирамиду DABC с вершинами в точках A,B,C,D
и, выбрав в качестве основания пирамиды ABC , определить
или составить:
2.1.Возможные уравнения плоскости, содержащей точки A,B,C .
2.2.Возможные уравнения прямой l1 , проходящей через точки A
и B.
2.3.Площадь ABC .
2.4.В ABC найти высоту СE , опущенную из вершины С на сторону AB, координаты основания высоты (точки E ) и со-
ставить уравнение прямой lCE , содержащей эту высоту.

310 |
Расчетно-графическая работа |
2.5.В ABC найти длину медианы СМ и составить уравнение прямой lCМ , содержащей медиану СМ .
2.6.В ABC найти биссектрису СК угла ACB и составить уравнение прямой lCК , содержащей биссектрису. Задачу ре-
шить двумя способами.
3.Расчеты в пирамиде DABC .
3.1.Составить уравнение прямой lDH , содержащей высоту пира-
миды DH и найти ее длину. Задачу решить двумя способами.
3.2.Найти объем пирамиды DABC (двумя способами).
3.3.Найти угол между гранями ABC и ADB.
3.4.Найти угол между ребром DA и основанием пирамиды.
4.Составить уравнения скрещивающихся прямых lCD и lAB .
4.1.Найти угол между прямыми lCD и lAB .
4.2.Найти расстояние между скрещивающимися прямыми (двумя способами).
● Комментарий к решению задач
Задача 1. Выберем четыре точки, так, чтобы они не лежали ни в одной из координатных плоскостей A1, 1, 2 , B 1, 2,3 , C 3,2,3 ,
D 1, 3,4 .
1.1. Проверим, не лежат ли точки A,B,C,D в одной плоскости. Для этого следует рассмотреть три вектора AB, AC, AD и если век-
торы компланарны, то точки будут принадлежать одной плоскости.
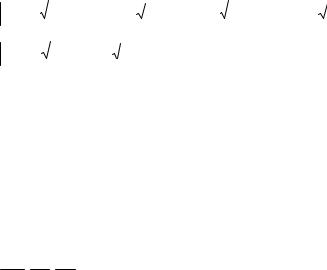
Так как AB 2, 1,5 , AC 2,3,5 , AD 0, 2,6 и
|
|
|
|
|
|
|
|
|
Расчетно-графическая работа |
311 |
|||
|
|
|
|
|
|
|
|
2 |
1 |
5 |
|
64 0, |
|
|
|
|
|
|
|
|
|
||||||
|
, |
|
, |
|
|
2 |
3 |
5 |
|
|
|||
AB |
AC |
AD |
|
||||||||||
|
|
0 |
2 |
6 |
|
|
|
||||||
то точки A,B,C,D в одной плоскости не лежат.
1.2. Проверим, не является ли ABC равнобедренным. Для этого
найдем длины сторон треугольника:
|
|
22 12 52 |
|
|
|
|
|
|
22 32 52 |
|
|
|
||
AB |
|
30, |
AC |
|
38, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 62 |
|
. |
|
|
|
|
|
|
|
|
|
AD |
|
40 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Среди сторон нет равных, и поэтому ABC не является равнобед-
ренным.
2. Рассмотрим ABC.
2.1. Составим различные уравнения плоскости 1 , содержащей точ-
ки A,B,C .
Общее уравнение плоскости, найдем как уравнение плоско-
сти, проходящей через три точки (условие компланарности векторов
|
AM, AB,AC): |
|
||
|
x 1 |
y 1 |
z 2 |
|
|
|
|||
|
2 |
1 |
5 |
0 |
|
2 |
3 |
5 |
|
или x 1 20 y 1 20 z 2 4 0, или
5x 5y z 8 0.
312 |
Расчетно-графическая работа |
Параметрическое уравнение плоскости 1 . Начальной точ-
кой плоскости выберем точку A , а в качестве направляющих векто-
ров плоскости возьмем векторы AB,AC . Параметрическое уравне-
ние плоскости 1 имеет вид
x 1 2t 2 , |
|
|
R,t R . |
y 1 t 3 , |
|
|
|
z 2 5t 5 , |
|
Нормированное уравнение плоскости 1 получим умножени-
ем общего уравнения плоскости на нормирующий множитель
|
|
|
1 |
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|||
52 |
52 |
12 |
51 |
|
||||||
Оно имеет следующий вид:
1 5x 5y z 8 0 
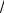 51
51
Уравнение плоскости в отрезках получим из общего уравне-
ния:
x |
|
y |
|
z |
1. |
|
8 |
8 |
1 |
||||
|
|
|
||||
5 |
|
5 |
|
5 |
|
2.2. Выпишем различные виды уравнения прямой l1 , проходящей через точки A и B . Примем за начальную точку прямой точку A, а
вектор q1 AB 2, 1,5 возьмем в качестве направляющего век-
тора возьмем.
