5. Первый и второй замечательные пределы

• Если угол выражен в радианах, то предел виданазываетсяпервым замечательным пределом.

Если функция содержит тригонометрические функции, то дляраскрытия неопределенности следует применить «первый замечательный предел» или его следствия, используя различные тригонометрические преобразования.

Пример 1. Вычислить предел:

.

• Предел вида называетсявторым замечательным пределом.

Число иррациональное и приближенно равно.

Неопределенность раскрывается с применением второго замечательного предела.

Пример 2. Вычислить предел: .

Логарифмы с основанием называютсянатуральными логарифмами, и обозначаются .

Связь десятичного логарифма с натуральным логарифмом:

.

Показательная функция с основаниемназываетсяэкспонентой.

Следствия.

; ;;;

; ;.

6. Эквивалентные бесконечно малые функции

• Две бесконечно малые функции иназываютсяэквивалентными в точке , если они ведут себя «одинаково» в данном процессе, т.е. предел их отношения равен единице. Записывается это так:.

Пример 3. . Значит,.

Таблица эквивалентных бесконечно малых функций при

; ;;;;

; ;;

; .

Указанные эквивалентности полезно использовать при вычислении пределов функций, используя следующее свойство: «Предел отношения двух бесконечно малых функций в точке не изменится, если каждую из них заменить эквивалентной б. м. функцией:».

Пример 4. Вычислить предел, применяя эквивалентные бесконечно малые функции.

7. Непрерывность функции, точки разрыва

Наиболее важным классом функций является класс непрерывных функций.

Можно считать функцию непрерывной в точке , если в этой точке отсутствует разрыв функции.

Что же это такое – разрыв функции? Рассмотрим несколько примеров.

Пример 5. Точка устранимого разрыва

Функция имеет конечный предел справаи конечный предел слева. Эти пределы равны, но значение функции в точкене существует (эта точка на кривой«выколота»). Эту точкуможно в кривую «вставить». Точка называетсяточкой устранимого разрыва

Пример 6. Точка неустранимого разрыва 1-го рода

Конечные пределы функции в точкеи справа, и слева существует, но они не равны. Функция в этой точке делает «скачок», равный . Точка называетсяточкой разрыва 1-го рода.

Пример 7. Точка разрыва 2-го рода

Функция не имеет конечных пределов ни справа, ни слева (а может быть, только с одной стороны). Точканазываетсяточкой разрыва 2-го рода.

Итак, можно сделать вывод:

• Точка являетсяточкой непрерывности функции , если существуют конечные пределы справа и слева и эти пределы равны значению функции в этой точке, т.е.

.

Если же хотя бы одно равенство нарушено, тогда точка является точкой разрыва функции.

Существует равносильное определение непрерывности функции в точке.

• Функция называетсянепрерывной в точке , если она определена в точкеи существует конечный предел, равный значению функции в данной точке, т.е..

При исследовании функции на непрерывность в точке нужно проверить выполнение следующих условий:

1) функция определена в точке ,т.е. существует;

2) существуют равные между собой конечные односторонние пределы ;

3) односторонние пределы равны - значению функции в точке , т.е. выполняется равенство .

Если хотя бы одно из условий 1 – 3 не выполнено, то точка есть точка разрыва функции .

Непрерывные в точке функции имеют важные свойства.

1. Если функции инепрерывны в точке, то их алгебраическая сумма, произведение и частное тоже непрерывны в этой точке.

2. Под знаком непрерывной функции можно переходить к пределу:.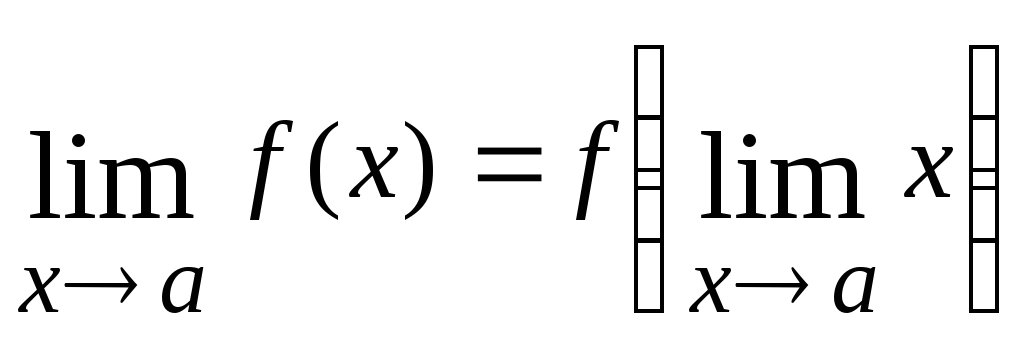

Это значит, что для непрерывной функции возможна перестановка символов предела и функции.

Элементарные функции непрерывны в каждой точке области их определения. Для всех основных элементарных функций в любой точке их области определения имеет место равенство

.

Отсюда следует:

1) точками разрыва элементарной функции являются те точки, в которых она не определена;

2) функция, не являющаяся элементарной, может иметь точки разрыва как в точках, в которых она не определена, так и в точках, в которых определена.

В частности, если функция задана несколькими аналитическими выражениями (формулами) для различных интервалов, то она может иметь разрывы в точках, где меняется ее аналитическое выражение.

Для сложной функции справедливо:

Если функция непрерывна в точке, а функциянепрерывная в точке, то сложная функциянепрерывна в точке, т.е.

.

Последняя формула показывает, что, с одной стороны, операция предельного перехода перестановочна с операцией взятия непрерывной функции (правое равенство), а с другой стороны, дает правило замены переменной при вычислении пределов непрерывных функций (левое равенство).

Пример 8.