6.2. Раскрытие неопределенностей различных типов

Далеко не всякая подстановка предельного значения в функцию вместо независимой переменной может сразу привести к нахождению предела. Случаи, в которых подстановка предельного значения в функцию не дает значения предела, называют неопределенностями; к ним относятся неопределенности видов

Устранить неопределенность удается часто с помощью алгебраических преобразований.

6.12. Найти

Решение. Имеем неопределенность вида [–]. Вынесем за скобкухв наибольшей степени:

х⁴является бесконечно большой величиной прих . По теоремам о пределах

так как иприх являются бесконечно малыми величинами, а предел постоянной равен самой постоянной (единице). По свойству бесконечно большихявляется бесконечно большой величиной, т.е. искомый предел равен.

Ответ данной задачи и приведенные в решении выкладки будем использовать при решении следующих примеров как заранее известные факты. Рассмотрим несколько типов примеров, классифицируя их по виду неопределенности и предельному значению х.

1-й тип. Рассмотрим примеры видас неопределенностью вида, гдеf(x)и(х)в общем случае – сложные степенные или показательные функции. В случае степенных функций необходимо выносить за скобку в числителе и знаменателе дробихс наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.

6.13. Найти

Решение. Вынося за скобку и в числителе и в знаменателехв наибольшей степени, получим

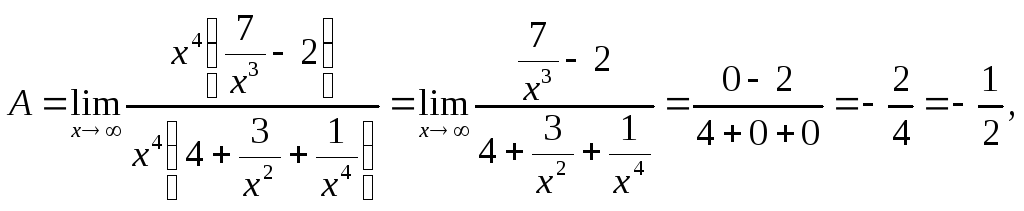
так как ,,, – величины бесконечно малые прих .

6.17. Найти

Решение. Припоказательная функция, пристремится к. Быстрее будет возрастать та функция, у которой основание больше, поэтому в нашем случае выносим за скобки:

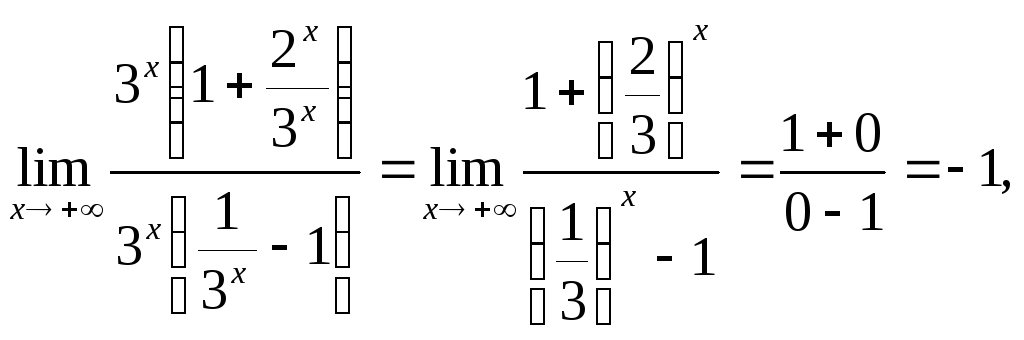
так как при и при.

Найти пределы:

6.18.

6.19.

6.20.

6.21.

6.22.

6.23.

6.24.

6.25.

6.26.

2-й тип. Рассмотрим примеры вида с неопределенностью видаВ этом случае необходимо разложить на множители и числитель, и знаменатель дроби или домножить и числитель, и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.

6.45.Найти

Решение.Имеем неопределенность видаРазложим числитель и знаменатель дроби на множители: числитель – по формуле сокращенного умноженияа знаменатель – по формуле разложения квадратного трехчлена на множители при

где

Получим

После сокращения дроби следует подставить предельное значение хв сокращенную дробь. Получим

6.46. Найти

Решение.1-й способ. Имеем неопределенность видаДополним числитель до разности квадратова знаменатель до разности кубовПолучим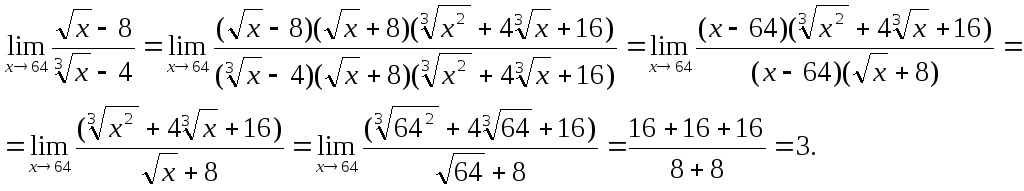

2-й способ. Сделаем замену переменной:тогдааприт.е.Теперь

Найти пределы:

6.47.

6.48.

6.49.

6.50.

6.51.

6.52.

6.53.

6.54.

6.55.

6.56.

6.57.

6.58.

3-й тип. Рассмотрим примеры с неопределенностью вида [∞ – ∞]. Если функция, стоящая под знаком предела, представляет собой алгебраическую сумму дробей, то неопределенность устраняется или приводится ко 2-му типу после приведения дробей к общему знаменателю. Если упомянутая функция представляет собой алгебраическую сумму иррациональных выражений, то неопределенность или устраняется, или приводится к 1-му типу путем домножения и деления функции на одно и то же (сопряженное) выражение, приводящее к формулам сокращенного умножения.

6.68. Найти

Решение. Имеем неопределенность вида [∞ – ∞]. Приведем дроби к общему знаменателю:

Имеем предел 2-го типа, необходимо разложить на множители числитель дроби. Получим

6.69. Найти

Решение.Имеем неопределенность вида [∞ – ∞]. Домножим и разделим функцию, стоящую под знаком предела на сопряженное выражение, приводящее к разности квадратов:

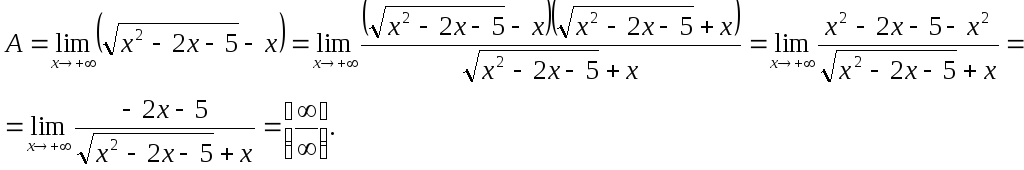
Имеем предел 1-го типа.

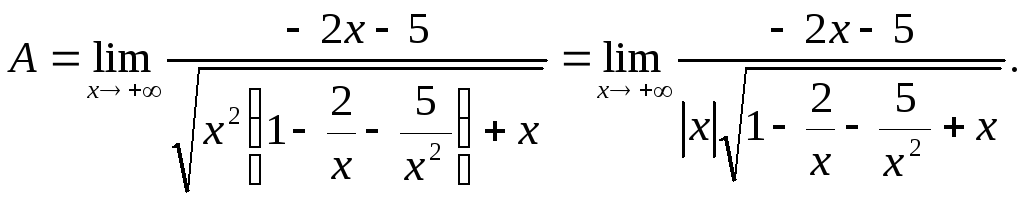
При по определению модуля; поэтому

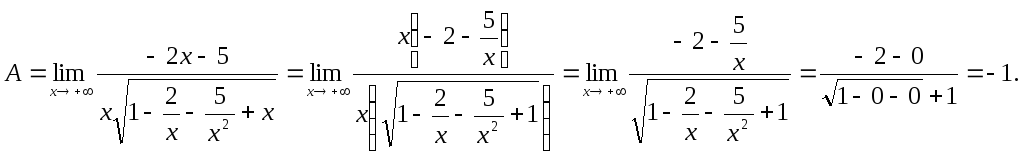
так как при - бесконечно малые величины.

Найти пределы:

6.70.

6.71.

6.72.

6.73.

6.74.

6.75.

6.76.

6.77.

6.78.

6.79.

6.80.

6.81.

6.82.

6.83.

6.84.

6.85.

6.86.

6.87.

6.3. Замечательные пределы

К пределам 4-го типаотнесем примеры с неопределенностью вида. В этом случае выражение, стоящее под знаком предела, представляет собой степенно-показательную функцию, в основании которой необходимо выделить целую часть дроби (которая должна быть равна 1). Неопределенность устраняется при помощи выделения «второго замечательного предела» .

6.97. Найти

Решение.Имеем неопределенность вида, так как

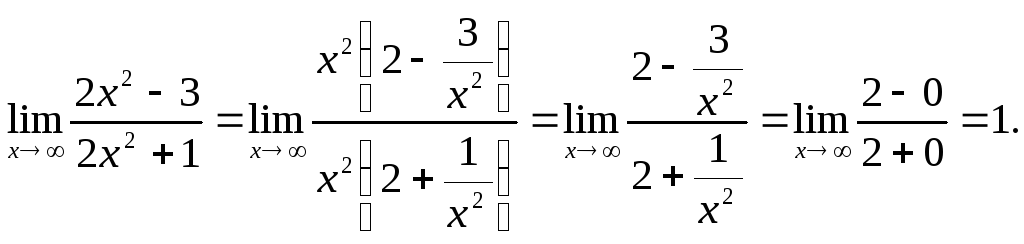
Выделим целую часть дроби

является бесконечно малой величиной прих → ∞. Домножим показатель степени наэто действие не нарушает знака равенства:

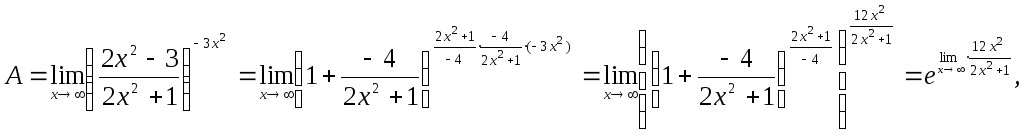
ибо НайдемИмеем неопределенность видапредел 1-го типа. Вынесем за скобких², так как вторая степень наибольшая:

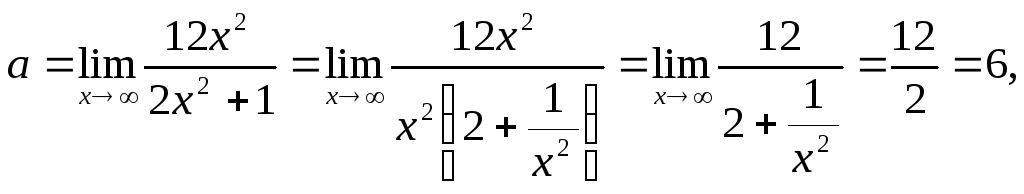
так как Таким образом предел равен

6.99. Найти

Решение.Имеем неопределенность видапреобразуем ее в неопределенность вида, пользуясь свойствами логарифмов:

Получим

Учитывая непрерывность логарифмической функции, символы limиlnможно переставить , получим

так как по формуле

Найти пределы:

6.100.

6.101.

6.102.

6.103.

6.104.

6.105.

6.106.

6.107.

6.108.

5-й тип.К этому типу отнесем функции, сводящиеся к первому замечательному пределу (6.1):

6.121. Найти

Решение.

Первый сомножитель представляет собой первый замечательный предел и равен 1, второй сомножитель представляет предел, равный . Таким образом, искомый предел равен 11 = 1.

6.122. Найти

Решение.Имеем неопределенность видаСделаем замену переменной:

arcsin х=у; тогдах = sinу; прих→ 0,у→0; получим

Имеем первый замечательный предел, следовательно искомый предел равен 1, что и требовалось доказать.

Найти пределы:

6.124.

6.125.

6.126.

6.127.

6.128.

6.129.

6.130.

6.131.

6.132.

6.133.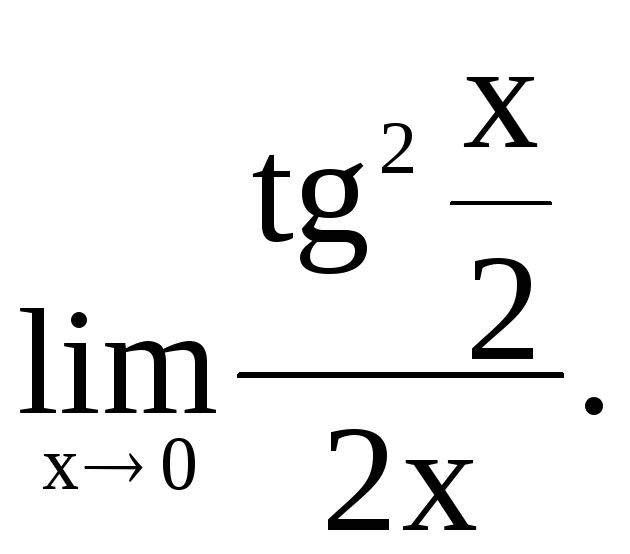

6.134.

6.135.

He рассмотренные в этой главе неопределенности видов [0], [0°] и [°] могут быть устранены при помощи правила Лопиталя, которое будет рассмотрено в главе 8.