- •Аналитическая геометрия
- •§1 Векторы………………………………………………………………..8
- •§1 Векторы.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №1.
- •§2 Прямая на плоскости.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №2.
- •§3 Прямая и плоскость в пространстве.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №3.
- •§4 Кривые 2-го порядка.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №4.
- •Аналитическая геометрия практикум по решению задач
- •426034, Ижевск, Университетская, д. 1, корп. 4, каб. 207
§4 Кривые 2-го порядка.
В аналитической геометрии на плоскости подробно изучаются геометрические свойства эллипса, гиперболы и параболы, представляющих собой линии пересечения кругового конуса с плоскостями, не проходящими через его вершину. Эти линии часто встречаются во многих задачах естествознания и техники. Например, движение материальной точки под воздействием центрального поля силы тяжести происходит по одной из этих линий; в инженерном деле для конструирования прожекторов, антенн и телескопов пользуются важным оптическим свойством параболы, заключающимся в том, что лучи света, исходящие из определённой точки (фокуса параболы), после отражения от параболы образуют параллельный пучок.
Определение.
Кривой
второго порядка
называется геометрическое место точек
координатной плоскости, координаты
которых удовлетворяют алгебраическому
уравнению 2-й степени с двумя
неизвестными:
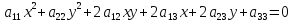 .
.
ОКРУЖНОСТЬ.
Определение. Окружностью называется геометрическое место точек плоскости равноудаленных от одной фиксированной точки плоскости, называемой центром окружности.
Определение. Расстояние от любой точки окружности до ее центра называется радиусом окружности.
Теорема.
Окружность является кривой 2-го порядка
и ее уравнение имеет вид:
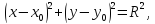 где
где
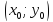 – координаты центра окружности,
– координаты центра окружности,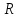 – радиус окружности.
– радиус окружности.
Определение.
Если центр окружности находится в начале
координат, то такая система координат
называется канонической
для окружности, а уравнение
 называется каноническим уравнением
окружности.
называется каноническим уравнением
окружности.
ЭЛЛИПС.
Определение.
Эллипсом
называется геометрическое место точек
плоскости, для которых сумма расстояний
до двух фиксированных точек плоскости,
называемых фокусами,
есть величина постоянная. Эту величину
принято обозначать через
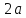 .
.
Определение.
Расстояние между фокусами эллипса
называется фокусным
расстоянием.
Фокусы эллипса принято обозначать
буквами
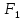 и
и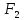 ,
расстояние между ними – через
,
расстояние между ними – через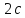 .
По определению эллипса
.
По определению эллипса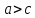 .
.
Определение.
Расстояния от точки
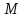 ,
лежащей на эллипсе, до фокусов
,
лежащей на эллипсе, до фокусов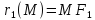 и
и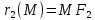 называютсяфокальными
радиусами
точки
называютсяфокальными
радиусами
точки
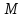 .
.
Замечание.
Из определения эллипса следует, что
точка
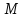 является точкой эллипса тогда и только
тогда, когда сумма её фокальных радиусов
является точкой эллипса тогда и только
тогда, когда сумма её фокальных радиусов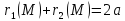 .
.
Определение.
Число
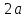 называетсябольшой
осью
эллипса, число
называетсябольшой
осью
эллипса, число
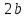 ,
где
,
где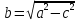 ,
называетсямалой
осью
эллипса. Числа
,
называетсямалой
осью
эллипса. Числа
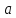 и
и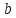 называются соответственнобольшой
и малой
полуосями
эллипса.
называются соответственнобольшой
и малой
полуосями
эллипса.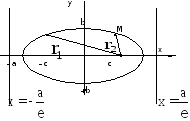
Определение.
Отношение фокусного расстояния эллипса
к его большой оси называется эксцентриситетом
эллипса, и обозначается буквой
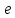 или
или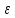 :
: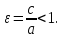
Определение. Ось, на которой лежат фокусы эллипса, называется фокальной осью эллипса.
В канонической для эллипса системе координат, оси координат являются главными осями эллипса, а начало координат является центром эллипса.
Определение. Точки эллипса, лежащие на его осях, называются вершинами эллипса.
Теорема.
(Каноническое уравнение эллипса.) Эллипс
является кривой 2-го порядка, и в
канонической для эллипса системе
координат его уравнение имеет вид: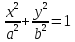 .
.
Теорема.
(Фокальные радиусы точки эллипса.) Пусть
в канонической для эллипса системе
координат точка
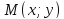 лежит на эллипсе. Тогда ее фокальные
радиусы равны:
лежит на эллипсе. Тогда ее фокальные
радиусы равны: ,
,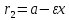 ,
где
,
где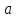 – большая полуось эллипса,
– большая полуось эллипса,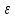 –
его эксцентриситет.
–
его эксцентриситет.
Определение.
В канонической для эллипса системе
координат прямые
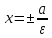 называютсядиректрисами
эллипса.
называютсядиректрисами
эллипса.
Теорема.
(Свойство директрис эллипса.) Пусть
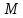 – произвольная точка эллипса,
– произвольная точка эллипса,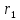 и
и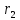 – ее фокальные радиусы. Обозначим через
– ее фокальные радиусы. Обозначим через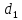 и
и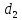 ,
соответственно, расстояния от точки
,
соответственно, расстояния от точки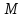 до левой и правой директрисы эллипса.
Тогда
до левой и правой директрисы эллипса.
Тогда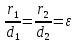 .
.
Теорема. (Зеркальное свойство эллипса.) Луч света, выпущенный из одного фокуса эллипса после отражения от зеркала эллипса проходит через второй его фокус.
Теорема.
В канонической для эллипса системе
координат уравнение касательной к
эллипсу в точке
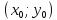 имеет вид:
имеет вид: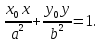
ГИПЕРБОЛА
Определение. Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний которых до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная.
Фокусы
гиперболы принято обозначать буквами
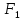 и
и .
Расстояния от точки
.
Расстояния от точки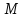 ,
лежащей на гиперболе, до фокусов
обозначаются
,
лежащей на гиперболе, до фокусов
обозначаются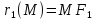 и
и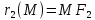 ,
и называются еёфокальными
радиусами.
,
и называются еёфокальными
радиусами.
Замечание.
Из определения гиперболы следует, что
точка М является точкой гиперболы тогда
и только тогда, когда модуль разности
её фокальных радиусов
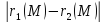 есть величина постоянная для данной
гиперболы. Эту константу принято
обозначать через
есть величина постоянная для данной
гиперболы. Эту константу принято
обозначать через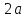 .
.
Определение. Расстояние между фокусами гиперболы называется фокусным расстоянием.
Фокусное
расстояние для данной гиперболы есть
величина постоянная и ее принято
обозначать через
 :
: .
.
Замечание.
Так как сторона треугольника больше
модуля разности двух его других сторон,
то отсюда и из определения гиперболы
следует, что
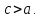
Определение.
Число
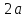 называетсядействительной
осью
гиперболы, число
называетсядействительной
осью
гиперболы, число
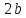 ,
где
,
где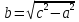 ,
называетсямнимой
осью
гиперболы. Числа
,
называетсямнимой
осью
гиперболы. Числа
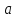 и
и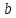 называются соответственнодействительной
и мнимой полуосями
гиперболы.
называются соответственнодействительной
и мнимой полуосями
гиперболы.
Определение.
Отношение фокусного расстояния гиперболы
к её действительной оси называется
эксцентриситетом
гиперболы, и обозначается буквой
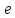 или
или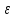 :
: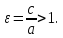
В канонической для гиперболы системе координат, оси координат являются главными осями гиперболы, а начало координат является центром гиперболы.
Теорема.
(Каноническое уравнение гиперболы.)
Гипербола является кривой 2-го порядка,
и в канонической для гиперболы системе
координат её уравнение имеет вид:
 .
.
Определение.
Точки
гиперболы, лежащие на её действительной
оси, называются действительными
вершинами
гиперболы. Две точки плоскости
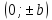 (в канонической для гиперболы системе
координат), лежащие на мнимой оси
гиперболы называютсямнимыми
вершинами
гиперболы.
(в канонической для гиперболы системе
координат), лежащие на мнимой оси
гиперболы называютсямнимыми
вершинами
гиперболы.
Определение.
Две пары прямых, параллельных осям
гиперболы
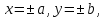 высекают прямоугольник, который
называетсяосновным
прямоугольником
гиперболы.
высекают прямоугольник, который
называетсяосновным
прямоугольником
гиперболы.
Гипербола
состоит из двух кривых, называемых её
ветвями,
которые в канонической системе
координат описываются уравнениями
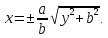
Теорема.
Прямые
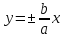 являются асимптотами гиперболы.
являются асимптотами гиперболы.
Теорема.
(Фокальные радиусы точек гиперболы.)
Пусть в канонической для гиперболы
системе координат точка
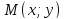 лежит на гиперболе. Тогда ее фокальные
радиусы равны:
лежит на гиперболе. Тогда ее фокальные
радиусы равны: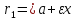 |,
|,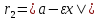 ,
где
,
где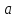 – действительная полуось гиперболы,
– действительная полуось гиперболы,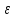 – её эксцентриситет.
– её эксцентриситет.
Определение.
В канонической для гиперболы системе
координат прямые
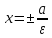 называютсядиректрисами
гиперболы.
называютсядиректрисами
гиперболы.
Теорема.
(Свойство директрис гиперболы.) Пусть
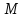 – произвольная точка гиперболы,
– произвольная точка гиперболы,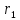 и
и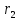 – ее фокальные радиусы. Обозначим через
– ее фокальные радиусы. Обозначим через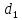 и
и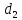 ,
соответственно, расстояния от точки
,
соответственно, расстояния от точки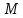 до левой и правой директрисы гиперболы.
Тогда
до левой и правой директрисы гиперболы.
Тогда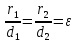 .
.

Теорема. (Зеркальное свойство гиперболы.) Луч света, выпущенный из одного фокуса гиперболы после отражения от зеркала гиперболы кажется наблюдателю идущим из второго её фокуса.
Теорема.
В канонической для гиперболы системе
координат уравнение касательной к
гиперболе в точке
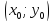 имеет вид:
имеет вид: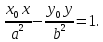
ПАРАБОЛА
Определение. Параболой называется геометрическое место точек плоскости, расстояние от которых до фиксированной прямой, называемой директрисой, равно расстоянию до фиксированной точки, называемой фокусом.
Определение.
Расстояние от произвольной точки
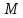 плоскости до фокуса параболы называетсяфокальным
радиусом точки
плоскости до фокуса параболы называетсяфокальным
радиусом точки
 .
.
Обозначения:
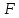 – фокус параболы,
– фокус параболы,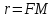 – фокальный радиус точки
– фокальный радиус точки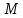 ,
,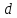 – расстояние от точки
– расстояние от точки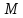 до директрисы
до директрисы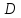 .
.
По
определению параболы, точка
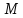 является точкой параболы тогда и только
тогда, когда
является точкой параболы тогда и только
тогда, когда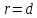 .
.
Определение.
Расстояние от фокуса параболы до ее
директрисы называется фокальным
параметром
параболы, и обозначается буквой
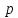 .
.
Замечание.
Из определений следует, что в канонической
для параболы системе координат фокус
имеет координаты
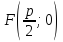 ,
а директриса описывается уравнением
,
а директриса описывается уравнением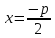 .
.
Теорема.
(Каноническое уравнение параболы.)
Парабола является кривой 2-го порядка,
и в канонической для неё системе координат
её уравнение имеет вид:
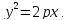
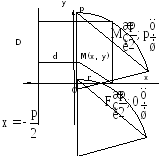
Теорема.
В канонической для параболы системе
координат, фокальный радиус точки
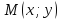 параболы равен
параболы равен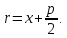
Теорема. (Зеркальное свойство параболы.) Луч света, выпущенный из фокуса параболы после отражения от зеркала параболы проходит параллельно её фокальной оси.
Теорема.
В канонической для параболы системе
координат уравнение касательной к
параболе в точке
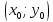 имеет вид:
имеет вид: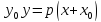 .
.
Определение. Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной.
Замечание.
Если координатная система выбрана так,
что ось абсцисс совмещена с осью параболы,
начало координат – с вершиной, но
парабола лежит в левой полуплоскости,
то ее уравнение будет иметь вид:
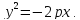
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, то парабола будет иметь уравнение:
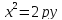 ,
если она лежит в верхней полуплоскости,
и
,
если она лежит в верхней полуплоскости,
и
 -
если в нижней полуплоскости.
-
если в нижней полуплоскости.
Полярная система координат.
Определение. Точка О называется полюсом, а луч L – полярной осью.
Задание какой-либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол называется полярным углом.
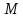
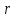
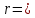
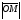
0
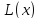
Можно
установить связь между полярной системой
координат и декартовой прямоугольной
системой, если поместить начало декартовой
прямоугольной системы в полюс, а полярную
ось направить вдоль положительного
направления оси
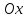 .
.
Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями:
x = rcos; y = rsin; x2 + y2 = r2.
Взаимосвязь
полярных и декартовых координат
определяется формулами:
 .
.
В
полярной системе координат уравнения
эллипса, параболы или правой ветви
гиперболы имеют вид:
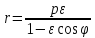 ,
причем, данное уравнение задает эллипс,
если
,
причем, данное уравнение задает эллипс,
если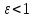 ;
параболу, если
;
параболу, если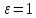 ;
гиперболу, если
;
гиперболу, если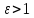 .
Левая ветвь гиперболы задается уравнением
.
Левая ветвь гиперболы задается уравнением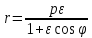 .
.
Инварианты кривых второго порядка.
Определение.
Инвариантами
уравнения линии второго порядка
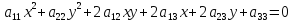 называются следующие выражения:
называются следующие выражения: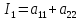 ,
,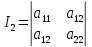 ,
,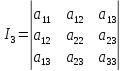 .
.
Определение.
Если инвариант
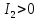 ,
то линия называется линией эллиптического
типа, если
,
то линия называется линией эллиптического
типа, если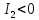 ,
то – гиперболического типа, если
,
то – гиперболического типа, если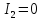 ,
то – параболического типа.
,
то – параболического типа.
Таблица для определения типа кривой второго порядка.
|
|
| ||||||||
|
|
|
|
| ||||||
|
|
|
|
|
|
парабола |
пара параллельных прямых | |||
|
эллипс |
точка |
|
гипербола |
пара пересекающихся прямых | |||||
Решение типовых задач.
Задача №1.
Составить
уравнение параболы, если даны её фокус
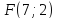 и директриса
и директриса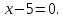
Решение:
I способ
Пусть
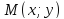 – произвольная точка параболы, тогда
(по определению параболы) расстояние
от точки
– произвольная точка параболы, тогда
(по определению параболы) расстояние
от точки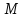 до фокусаF
равно её расстоянию
до фокусаF
равно её расстоянию
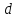 до директрисы.
до директрисы.
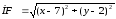
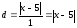
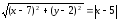
Возведём
в квадрат обе части, получим искомое
уравнение:
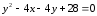
II способ
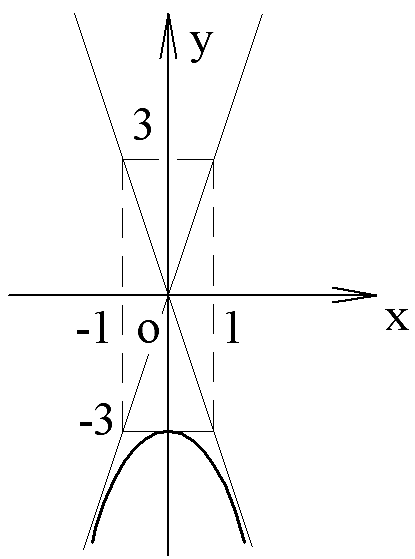
Сделаем чертёж:
|
Очевидно, осью симметрии параболы является прямая y = 2. Вершина
|
|
Совершим
параллельный перенос системы
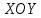 на вектор
на вектор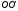 :
:
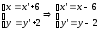
В
полученной системе координат
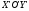 уравнение параболы имеет канонический
вид:
уравнение параболы имеет канонический
вид:
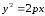 ,
где
,
где
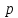 – расстояние между фокусом и директрисой,
– расстояние между фокусом и директрисой,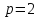 .
Тогда
.
Тогда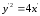 .
Из формул параллельного переноса
следует:
.
Из формул параллельного переноса
следует: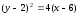 .
Поэтому уравнение параболы примет вид:
.
Поэтому уравнение параболы примет вид: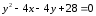 .
.
Ответ:
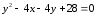 .
.
Задача №2.
Найти
фокус и директрису параболы
 .
.
Решение:
выразим из уравнения:
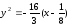 .
.
Сделаем
преобразование системы координат
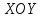 :
:
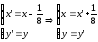 .
Тогда
.
Тогда
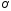
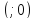 -
это преобразование есть параллельный
перенос.
-
это преобразование есть параллельный
перенос.
Уравнение
параболы в системе
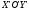 примет
вид:
примет
вид: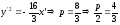
|
|
Очевидно,
в новой системе координат
|
Перейдём
к исходной системе координат: уравнение
директрисы: .
.
Фокус
F
имеет координаты:
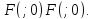
Ответ:
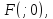
 .
.
Задача №3.
Точка
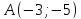 лежит на гиперболе, фокус которой
лежит на гиперболе, фокус которой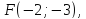 а соответствующая директриса задана
уравнением
а соответствующая директриса задана
уравнением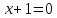 .
Составить уравнение этой гиперболы.
.
Составить уравнение этой гиперболы.
Решение:
Пусть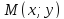 – произвольная точка гиперболы. По
теореме об отношении расстояний
(отношение расстоянияr
от любой точки гиперболы до фокуса к
расстоянию d
от этой точки до соответствующей
директрисы есть величина постоянная,
равная эксцентриситету гиперболы):
– произвольная точка гиперболы. По
теореме об отношении расстояний
(отношение расстоянияr
от любой точки гиперболы до фокуса к
расстоянию d
от этой точки до соответствующей
директрисы есть величина постоянная,
равная эксцентриситету гиперболы):
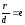 ,
,
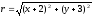 ;
;
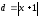 ,e
найдём, применив теорему для данной
точки
,e
найдём, применив теорему для данной
точки
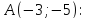 тогда
тогда
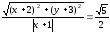 .
.
Сделав
соответствующие преобразования, получим
уравнение: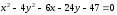 .
.
Ответ:
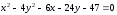 .
.
Задача №4.
Точка
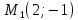 лежит
на эллипсе, фокус которого
лежит
на эллипсе, фокус которого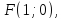 а соответствующая директриса задана
уравнением
а соответствующая директриса задана
уравнением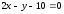 .
Составить уравнение этого эллипса.
.
Составить уравнение этого эллипса.
Решение:
Решение этой задачи аналогично предыдущей задачи.
Пусть
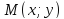 – произвольная точка эллипса. По теореме
об отношении расстояний имеем:
– произвольная точка эллипса. По теореме
об отношении расстояний имеем: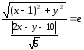 .
.
e
найдём по этой же теореме, используя
точку
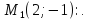
Тогда
уравнение эллипса примет вид:
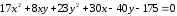 .
.
Ответ:
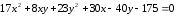 .
.
Задача №5.
Из
фокуса параболы
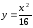 опущен перпендикуляр на прямую, проходящую
через центр эллипса
опущен перпендикуляр на прямую, проходящую
через центр эллипса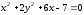 и составляющую с осью
и составляющую с осью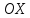 угол 135°. Составить уравнение этой прямой
и найти длину перпендикуляра.
угол 135°. Составить уравнение этой прямой
и найти длину перпендикуляра.
Решение:
Найдём координаты центра эллипса, для этого преобразуем его уравнение:
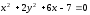 ;
;
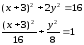 .
.
Итак,
координаты
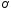 эллипса
эллипса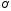
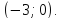 Прямая
проходит через точку
Прямая
проходит через точку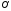 ,
угловой коэффициент прямой
,
угловой коэффициент прямой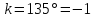 ,
поэтому уравнение прямой примет вид:
,
поэтому уравнение прямой примет вид: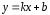 ,
т.е.
,
т.е.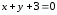 .
.
Найдём
фокус параболы
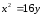 ,
т.е.
,
т.е.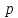 = 8, поэтому
= 8, поэтому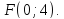
Искомая
длина перпендикуляра – это расстояние
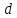 от фокуса до прямой
от фокуса до прямой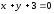 ,
поэтому
,
поэтому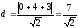 .
.
Ответ:
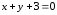 ,
,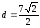 .
.
Задача №6.
Даны
вершина параболы
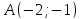 и уравнение её директрисы
и уравнение её директрисы .
Составить уравнение этой параболы.
.
Составить уравнение этой параболы.
Решение:
Найдём
фокус параболы, для этого опустим из
вершины
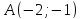 параболы перпендикуляр на директрису:
параболы перпендикуляр на директрису:
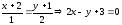 .
Эта прямая является осью симметрии
параболы.
.
Эта прямая является осью симметрии
параболы.
Найдём
точку
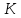 ,
пересечение оси симметрии параболы с
её директрисой:
,
пересечение оси симметрии параболы с
её директрисой: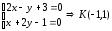 .
.
Фокус
параболы – это конец отрезка
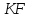 с известными началом
с известными началом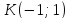 и серединой
и серединой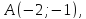 поэтому
поэтому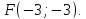 Зная фокус параболы и её директрису,
найдём её уравнение.
Зная фокус параболы и её директрису,
найдём её уравнение.
Ответ:
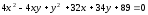 .
.
Задача №7.
Определить,
при каких значениях
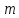 прямая
прямая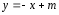 :
:
1)
пересекает эллипс
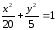 ;
;
2) касается его;
3) проходит вне этого эллипса.
Решение:
Решая
систему
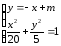 ,
получим уравнение
,
получим уравнение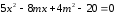 .
.
Чтобы прямая пересекала эллипс, нужно чтобы полученное квадратное уравнение относительно x имело два решения, для этого дискриминант D>0.
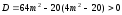 .
Откуда
.
Откуда
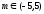 .
.
Чтобы прямая касалась эллипса, нужно чтобы
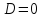 ,
т.е.
,
т.е.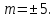
Нет пересечений, если
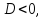 т.е.
т.е.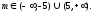
Ответ:1)
при
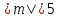 пересекает эллипс;
пересекает эллипс;
2)
при
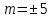 касается эллипса;
касается эллипса;
3)
при
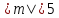 проходит вне эллипса.
проходит вне эллипса.
Задача №8.
Провести
касательные к эллипсу
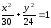 параллельно прямой
параллельно прямой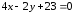 и вычислить расстояние между ними.
и вычислить расстояние между ними.
Решение:
Если
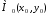 -
точка касания, то уравнение касательной
к эллипсу имеет вид:
-
точка касания, то уравнение касательной
к эллипсу имеет вид: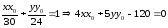 .
.
Угловой
коэффициент
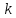 к
этой касательной равен:
к
этой касательной равен: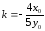 .
.
Но
касательная параллельна прямой
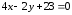 ,
поэтому
,
поэтому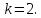 Поэтому, чтобы найти точки касания,
решим систему:
Поэтому, чтобы найти точки касания,
решим систему: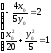 .
.
Оттуда
точка
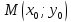 имеет координаты
имеет координаты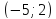 и
и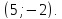 Поэтому, используя уравнение
Поэтому, используя уравнение ,
будем иметь уравнения касательных:
,
будем иметь уравнения касательных: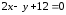 и
и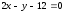 .
.
Расстояние
между касательными – это расстояние
от точки
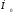
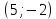 до второй касательной:
до второй касательной:
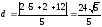 .
.
Ответ: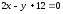 ,
,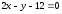 ,
,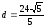 .
.
Задача №9.
Написать
уравнение эллипса, для которого прямые
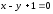 и
и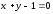 есть
соответственно большая и малая оси, и
длины полуосей которого
есть
соответственно большая и малая оси, и
длины полуосей которого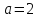 ,
,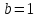 .
.
Решение:
Найдём
центр
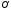 эллипса:
эллипса: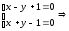
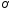
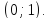
|
Обозначим
через
Через
В
этой системе координат эллипс задаётся
каноническим уравнением:
|
|
Повернём
систему
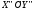 на угол, равный -45º, тогда система совпадёт
с системой
на угол, равный -45º, тогда система совпадёт
с системой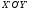 .
Формулы поворота:
.
Формулы поворота:
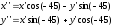 или
или
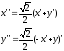 .
.
А
уравнение эллипса примет вид:
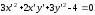 .
.
Сделаем
второе преобразование: параллельно
перенесём систему
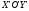 на вектор
на вектор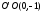 .
.
Формулы
параллельного переноса:
 .
.
Уравнение
эллипса в системе
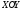 примет
вид:
примет
вид:
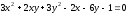 .
.
Ответ: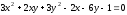 .
.
Задача №10.
Не
приводя преобразование координат,
установить, какой геометрический образ
определяет уравнение, и найти величины
его полуосей:
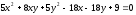 .
.
Решение:
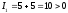 .
.
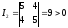 .
.
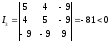 .
.
Итак, уравнение определяет эллипс. Составим характеристическое уравнение:
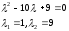 .
.
Тогда
преобразованное уравнение примет вид:
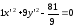 .
.
Откуда
каноническое уравнение примет вид:
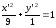 .
.
Ответ:
эллипс,
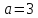 ,
,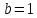 .
.
Задача №11.
Не
приводя преобразования координат,
установить тип кривой и найти величины
её полуосей:
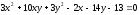 .
.
Решение:
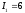
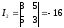

Уравнение
определяет гиперболу. Т.к.
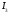 >0,
то действительной осью является ось
>0,
то действительной осью является ось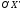 .
Составим характеристическое уравнение:
.
Составим характеристическое уравнение:
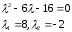 .
.
Каноническое
уравнение гиперболы:
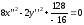 ,
т.е.
,
т.е.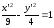 .
.
Ответ:
гипербола,
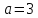 ,
,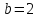 .
.
Задача №12.
Не
приводя преобразования координат,
установить тип кривой и найти величины
её полуосей: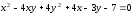 .
.
Решение:
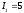 ,
,
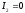 ,
,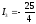 - парабола,
- парабола,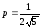 .
Каноническое уравнение:
.
Каноническое уравнение: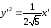 .
.
Ось
параболы определяется уравнением:
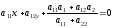 .
.
В
разбираемом случае имеем:
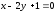 .
Вершину параболы находим как точку
пересечения линии с её осью из системы
уравнений:
.
Вершину параболы находим как точку
пересечения линии с её осью из системы
уравнений:
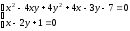 или
или
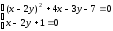 или
или
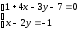 или
или
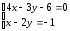 .
.
Вершина
параболы
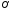
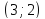 .
Единичный направляющий вектор оси
параболы в сторону вогнутости при
.
Единичный направляющий вектор оси
параболы в сторону вогнутости при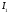
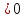 определяется уравнением и неравенством:
определяется уравнением и неравенством: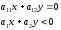 .
.
В
рассматриваемом случае имеем:
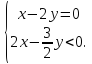
Имеем:
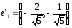 ;
; .
.
Ответ:
парабола,
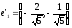 ;
;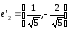 .
.
Задача №13.
Не
приводя преобразования координат,
установить тип кривой и найти величины
её полуосей: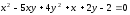 .
.
Решение:
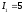 ,
,
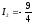 ,
,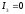 - пересекающиеся прямые. Точка пересечения
находиться как центр линий:
- пересекающиеся прямые. Точка пересечения
находиться как центр линий: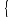
Точка
пересечения
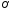
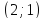 .
Направляющие векторы прямых находятся
как векторы асимптотических направлений:
.
Направляющие векторы прямых находятся
как векторы асимптотических направлений: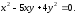
Направляющие
векторы прямых:
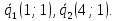
Уравнения прямых:
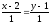 и
и
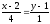 или
или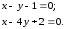
Ответ:
пересекающиеся прямые:
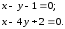
Задача №14.
Не
приводя преобразования координат,
установить тип кривой и найти величины
её полуосей:
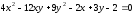
Решение:
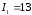 ,
,
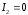 ,
,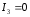 -
пара прямых (действительных, мнимых или
совпадающих).
-
пара прямых (действительных, мнимых или
совпадающих).
Чтобы
решить, какие это прямые, достаточно
найти точки пересечения данной линии
с осью
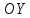 .
.
Имеем:
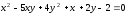 ,x
= 0, или
,x
= 0, или
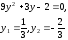 -
действительные параллельные прямые.
Направляющие векторы прямых имеют
асимптотические направления и находятся
из уравнения:
-
действительные параллельные прямые.
Направляющие векторы прямых имеют
асимптотические направления и находятся
из уравнения: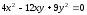 .
.
Направляющие
векторы прямых
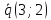 .
Их угловой коэффициент
.
Их угловой коэффициент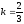 .
Уравнения прямых:
.
Уравнения прямых: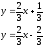 или
или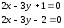 .
.
Ответ:
параллельные прямые:
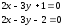 .
.
Задача №15.
Установить, какие линии определяются следующими уравнениями:
1)
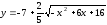 ;
;
2)
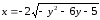 .
.
Решение:
1)
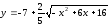 .
.
ОДЗ:
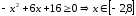 ;
;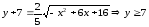 .
.
После
преобразований уравнение эллипса
принимает вид:
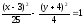 .
.
Итак,
координаты центра эллипса
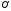
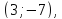 полуоси
полуоси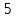 и
и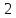 .
Учитывая, что
.
Учитывая, что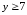 ,
можно сказать, что искомой линией
является половина эллипса, расположенная
над прямой
,
можно сказать, что искомой линией
является половина эллипса, расположенная
над прямой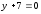 .
.
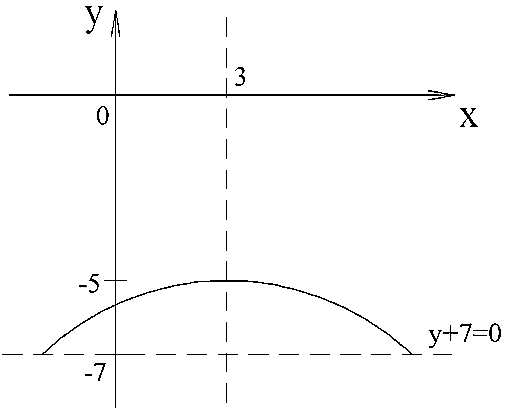
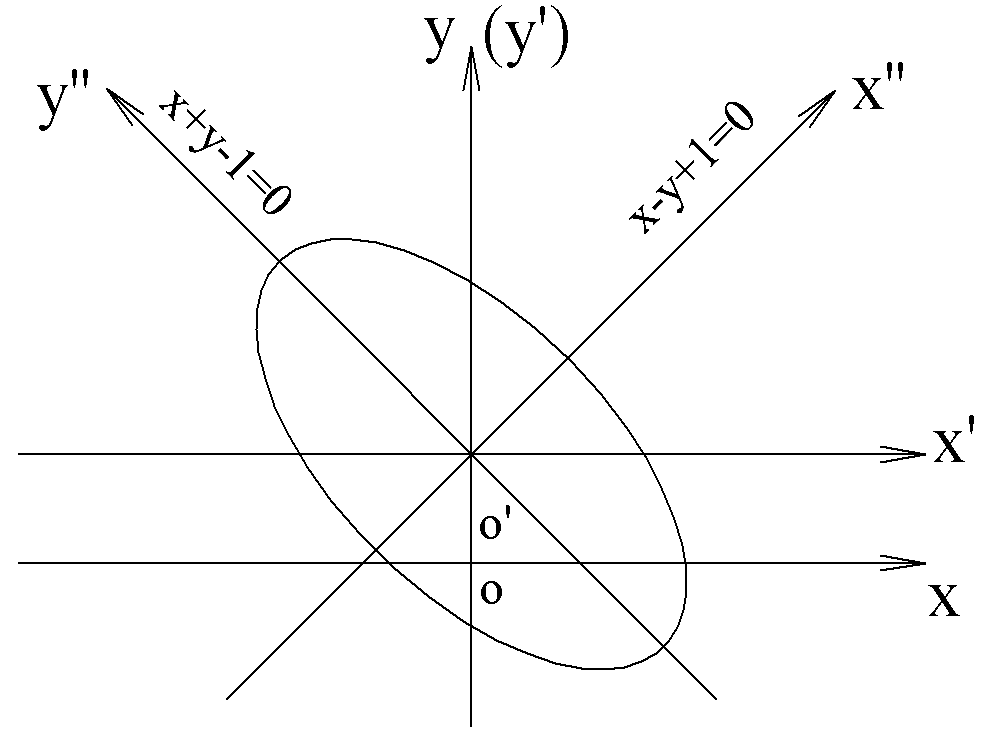
2)
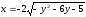 .
.
|
|
ОДЗ:
|
| |
|
|
Т.к.
Итак, преобразуем уравнение:
Центр
эллипса
Ответ: половина эллипса
в левой полуплоскости. | ||
Задача №16.
Определить, какие линии определяются следующими уравнениями:
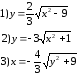
Изобразить линии на чертеже.
Решение:
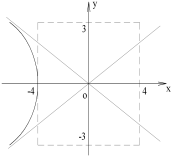
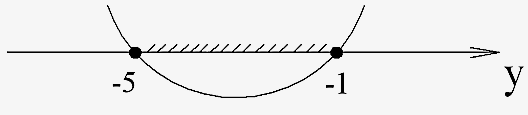
1)
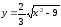
ОДЗ:
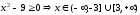 ,
,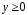 .
.
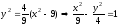
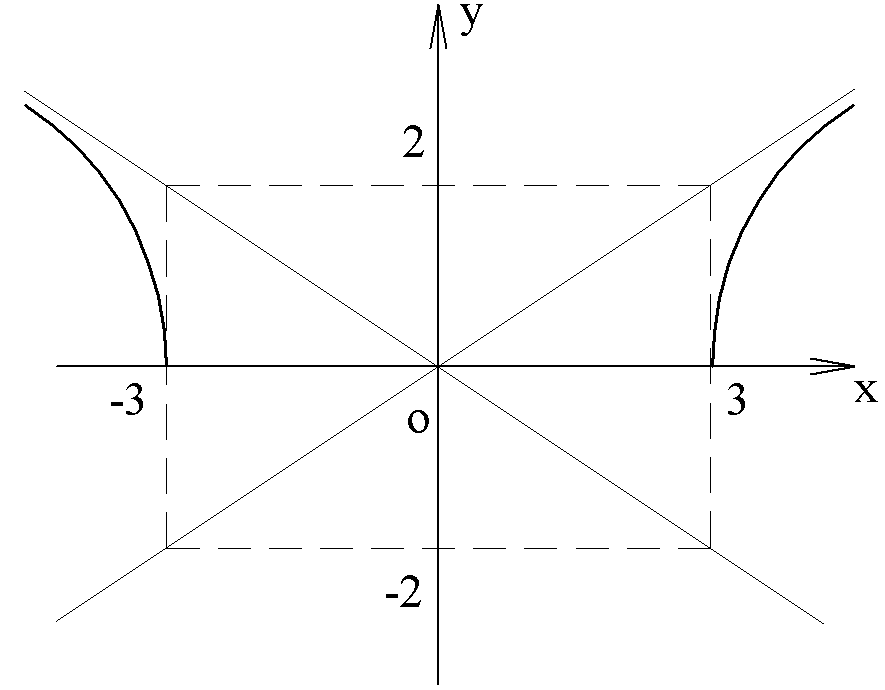
Ответ:
часть гиперболы
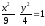 ,
расположенная в верхней полуплоскости.
,
расположенная в верхней полуплоскости.
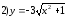
|
Ответ:
ветвь гиперболы
|
|
|
|

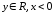 .
.
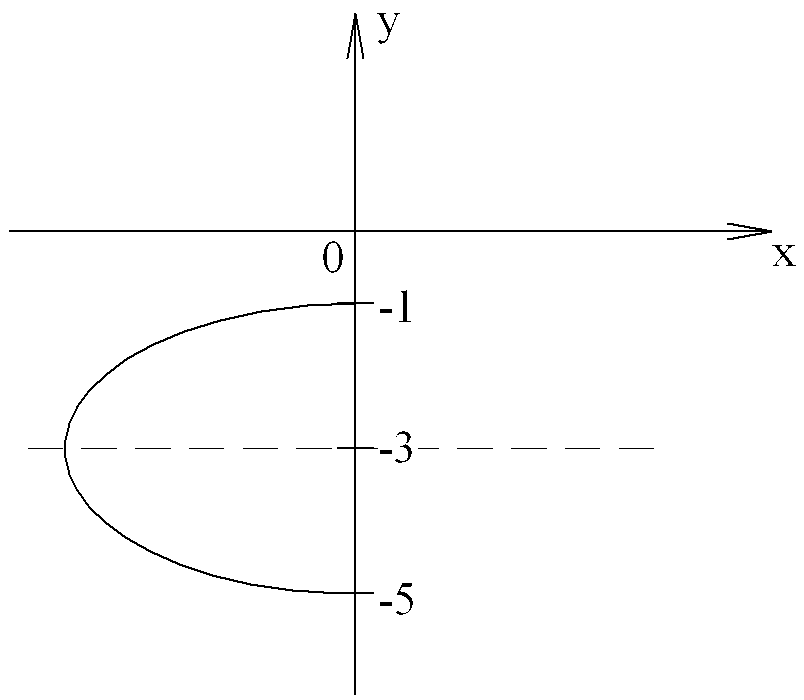
Ответ: Ветвь гиперболы
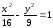 ,
расположенная
,
расположенная
в левой полуплоскости.
Задача №17.
Уравнение
кривой в полярной системе координат
имеет вид:
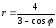 .
Найти уравнение кривой в декартовой
прямоугольной системе координат,
определит тип кривой, найти фокусы и
эксцентриситет. Схематично построить
кривую.
.
Найти уравнение кривой в декартовой
прямоугольной системе координат,
определит тип кривой, найти фокусы и
эксцентриситет. Схематично построить
кривую.
Решение.
Воспользуемся
связью декартовой прямоугольной и
полярной системы координат:
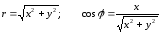 ;
;
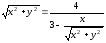 ;
;
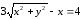 ;
;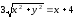
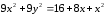 ;
;
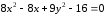 ;
;
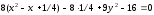 ;
;
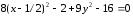 ;
;
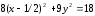 ;
;
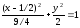 .
.
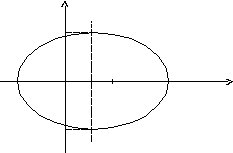
Получили
каноническое уравнение эллипса. Из
уравнения видно, что центр эллипса
сдвинут вдоль оси
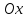 на
на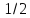 вправо, большая полуосьa
равна
вправо, большая полуосьa
равна
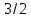 ,
меньшая полуось
,
меньшая полуось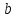 равна
равна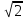 ,
половина расстояния между фокусами
равно
,
половина расстояния между фокусами
равно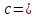
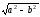
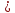 1/2.
Эксцентриситет равен
1/2.
Эксцентриситет равен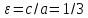 .
Фокусы
.
Фокусы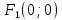 и
и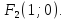
y
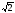
F1 F2
-1 0
½ 1 2
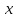
-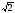
Образовательным результатом после изучения данной темы является сформированность компонент, заявленных во введении, совокупности компетенций (знать, уметь, владеть) на двух уровнях: пороговый и продвинутый. Пороговый уровень соответствует оценке «удовлетворительно», продвинутый уровень соответствует оценкам «хорошо» или «отлично» в зависимости от результатов защиты кейс-заданий.
Для самостоятельной диагностики данных компонент вам предлагаются следующие задания.

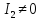
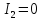
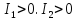
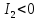
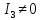
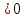
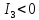
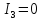
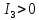
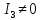
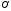 параболы
находится на этой оси на одинаковом
расстоянии от фокуса и директрисы,
т.е. имеет координаты
параболы
находится на этой оси на одинаковом
расстоянии от фокуса и директрисы,
т.е. имеет координаты
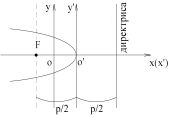
 уравнение директрисы имеет вид:
уравнение директрисы имеет вид: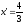 .
Фокус
.
Фокус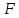 имеет координаты
имеет координаты
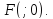
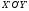 систему координат, началом которой
является точка
систему координат, началом которой
является точка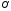
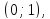 а
оси параллельны осям
а
оси параллельны осям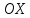 и
и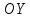 .
.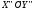 обозначим систему координат с началом
в точке
обозначим систему координат с началом
в точке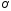
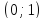 и осями координат, совпадающими с
осями эллипса.
и осями координат, совпадающими с
осями эллипса.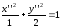
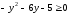
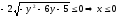
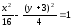
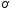
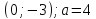 ,
,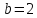 .
.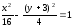 ,
расположенная
,
расположенная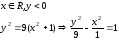
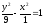 ,
расположенная в нижней полуплоскости.
,
расположенная в нижней полуплоскости.