
- •Аналитическая геометрия
- •§1 Векторы………………………………………………………………..8
- •§1 Векторы.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №1.
- •§2 Прямая на плоскости.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №2.
- •§3 Прямая и плоскость в пространстве.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №3.
- •§4 Кривые 2-го порядка.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №4.
- •Аналитическая геометрия практикум по решению задач
- •426034, Ижевск, Университетская, д. 1, корп. 4, каб. 207
§2 Прямая на плоскости.
Определение.
Любой ненулевой вектор, перпендикулярный
прямой называется её нормальным
вектором,
и обозначается
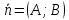 .
.
Теорема. Алгебраическое уравнение 1-й степени
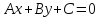 ,
,
где
коэффициенты
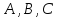 – произвольные действительные числа,
одновременно не равные нулю, являетсяуравнением
прямой на плоскости
– произвольные действительные числа,
одновременно не равные нулю, являетсяуравнением
прямой на плоскости
 ,
а вектор
,
а вектор
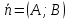 является её нормальным вектором.
является её нормальным вектором.
Верно
обратное:
на координатной плоскости
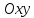 уравнение
любой прямой с нормальным вектором
уравнение
любой прямой с нормальным вектором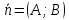 ,
может быть записано в виде алгебраического
уравнения
,
может быть записано в виде алгебраического
уравнения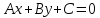 .
.
Определение. Уравнение прямой вида
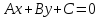 ,
,
где
коэффициенты
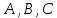 – произвольные действительные числа,
одновременно не равные нулю, называетсяобщим
уравнением прямой.
– произвольные действительные числа,
одновременно не равные нулю, называетсяобщим
уравнением прямой.
Известно,
что прямая определяется двумя точками.
Пусть
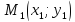 и
и
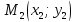 –
точки, лежащие на прямой
–
точки, лежащие на прямой
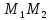 ,
,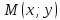 –
произвольная точка этой прямой. Тогда
векторы
–
произвольная точка этой прямой. Тогда
векторы
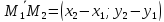 и
и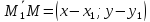 – коллинеарны, а их координаты
пропорциональны. Получаемуравнение
прямой, проходящей через две точки:
– коллинеарны, а их координаты
пропорциональны. Получаемуравнение
прямой, проходящей через две точки:
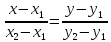 .
.
Определение. Вектор, параллельный прямой, называется направляющим вектором прямой.
Определение.
Пусть
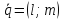 – направляющий вектор прямой. Тогда из
предыдущего уравнения получаемканоническое
уравнение прямой:
– направляющий вектор прямой. Тогда из
предыдущего уравнения получаемканоническое
уравнение прямой:
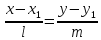 .
.
Определение.
В
тех же обозначениях, параметрическое
уравнение прямой
имеет вид:
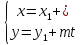 .
.

Определение.
Уравнение прямой вида
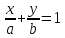 ,
где
,
где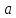 и
и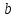 – произвольные, не равные нулю
действительные числа, называетсяуравнением
прямой в отрезках.
– произвольные, не равные нулю
действительные числа, называетсяуравнением
прямой в отрезках.
Теорема.
Пусть
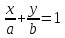 – уравнение прямой в отрезках. Тогда
– уравнение прямой в отрезках. Тогда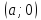 ,
,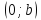 – координаты точек пересечения данной
прямой с осями координат.
– координаты точек пересечения данной
прямой с осями координат.
Определение.
Уравнение прямой вида
 ,
где
,
где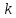 и
и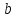 – произвольные действительные числа,
называетсяуравнением
прямой с угловым коэффициентом,
коэффициент
– произвольные действительные числа,
называетсяуравнением
прямой с угловым коэффициентом,
коэффициент
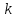 называетсяугловым
коэффициентом данной
прямой.
называетсяугловым
коэффициентом данной
прямой.
Теорема.
Пусть
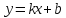 – уравнение прямой с угловым коэффициентом.
Тогда
– уравнение прямой с угловым коэффициентом.
Тогда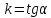 ,
где угол
α
равен углу наклона данной прямой к оси
,
где угол
α
равен углу наклона данной прямой к оси
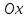 ,
,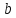 – ордината точки пересечения с осью
– ордината точки пересечения с осью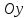 .
.
Если
известны угловые коэффициенты
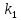 и
и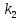 двух прямых, то один из углов
двух прямых, то один из углов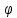 между этими прямыми определяется по
формуле:
между этими прямыми определяется по
формуле:
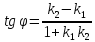 .
.
Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:
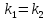 .
.
Признаком
перпендикулярности двух прямых является
соотношение:
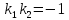 или
или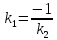 .
.
Теорема. (Связь нормального вектора прямой с её направляющим вектором и её угловым коэффициентом.)
1)
Если
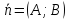 – нормальный вектор прямой, то
– нормальный вектор прямой, то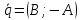 – её направляющий вектор, и, если
– её направляющий вектор, и, если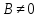 ,
то
,
то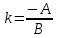 – её угловой коэффициент.
– её угловой коэффициент.
2)
Если
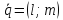 – направляющий вектор прямой, то
– направляющий вектор прямой, то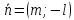 – её нормальный вектор, и, если
– её нормальный вектор, и, если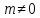 , то
, то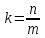 – её угловой коэффициент.
– её угловой коэффициент.
3)
Если
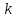 угловой коэффициент прямой, то
угловой коэффициент прямой, то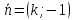 – её нормальный вектор,
– её нормальный вектор,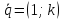 –
направляющий вектор.
–
направляющий вектор.
Взаимное расположение двух прямых на плоскости.
Две прямые на плоскости могут пересекаться, совпадать или быть параллельными.
Теорема. Пусть прямые заданы общими уравнениями:
L1: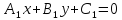 ,L2:
,L2: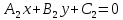 .
Тогда:
.
Тогда:
1)
если
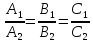 ,
то прямые совпадают, и система уравнений
,
то прямые совпадают, и система уравнений
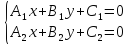
имеет бесконечное множество решений;
2)
если
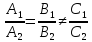 , то прямые параллельные, и система
уравнений
, то прямые параллельные, и система
уравнений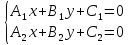 не имеет решений;
не имеет решений;
3)
если
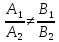 , то прямые пересекаются и координаты
точки их пересечения являются единственным
решением системы уравнений
, то прямые пересекаются и координаты
точки их пересечения являются единственным
решением системы уравнений
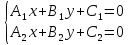 .
.
Определение.
Уравнение вида
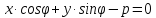 ,
где
,
где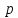 – расстояние от прямой до начала
координат, называетсянормальным
уравнением прямой,
– расстояние от прямой до начала
координат, называетсянормальным
уравнением прямой,
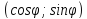 – координаты орта вектора
– координаты орта вектора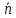 .
.
Чтобы
привести прямую к указанному виду,
разделим общее уравнение прямой на
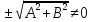 , причем со знаком «+» в случае, когда
, причем со знаком «+» в случае, когда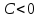 , и со знаком «-» в случае, когда
, и со знаком «-» в случае, когда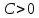 , получим:
, получим:
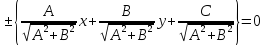 .
.
Теорема.
Орт нормального вектора
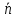 имеет координаты:
имеет координаты:
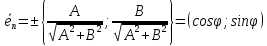 ,
,
где
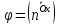 .
.
Теорема.
Расстояние от прямой до произвольной
точки
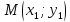 находится
по формуле:
находится
по формуле:
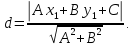
Чтобы найти расстояние между двумя параллельными прямыми, нужно взять произвольную точку на одной из прямых и найти расстояние от нее до другой прямой.
Чтобы
найти множество
точек, равноудаленных от двух прямых
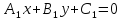 и
и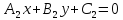 , составим уравнение:
, составим уравнение:
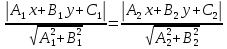 .
.
Раскрывая модули в случае параллельных прямых, получаем параллельную им прямую, лежащую между данными прямыми, а в случае пересекающихся прямых – биссектрисы углов, образованных пересечением прямых.
Определение. Совокупность прямых, проходящих через некоторую точку S, называется пучком прямых с центром S.
Теорема.
Если
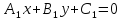 и
и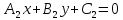 – уравнения двух прямых, пересекающихся
в точкеS,
то уравнение:
– уравнения двух прямых, пересекающихся
в точкеS,
то уравнение:
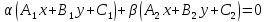 ,
,
где
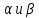 – какие угодно числа, не равные
одновременно нулю, определяют прямую,
также проходящую через точкуS.
– какие угодно числа, не равные
одновременно нулю, определяют прямую,
также проходящую через точкуS.
Более того, в указанном уравнении числа всегда возможно подобрать так, чтобы оно определяло любую (заранее назначенную) прямую, проходящую через точку S, иначе говоря, любую прямую пучка с центром S. Поэтому уравнение вида называется уравнением пучка с центром S.
Решение типовых задач
Задача №1:
Даны
уравнения двух сторон параллелограмма
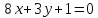 ,
,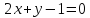 и уравнение одной из его диагоналей
и уравнение одной из его диагоналей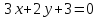 .
Определить координаты вершин этого
параллелограмма.
.
Определить координаты вершин этого
параллелограмма.
Решение:

Найдём
координаты т.
 как точки пересечения прямых
как точки пересечения прямых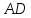 и
и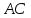 :
: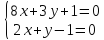 ;
;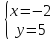 ;
т.
;
т.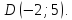 Выясним, какая из диагоналей задана.
Выясним, какая из диагоналей задана.
Подставим
координаты т.
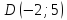 в уравнение диагонали
в уравнение диагонали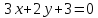 :
: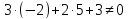 ;
т.
;
т.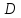 не принадлежит заданной диагонали,
следовательно
не принадлежит заданной диагонали,
следовательно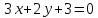 – уравнение диагонали
– уравнение диагонали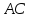 .
.
Найдём
координаты т.
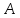 ,
как точки пересечения
,
как точки пересечения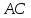 и
и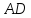 :
:
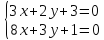 ;
;
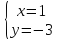 ;
т.
;
т.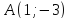 .
.
Найдём
координаты т.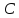 ,
как точки пересечения
,
как точки пересечения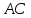 и
и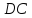 :
:
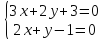 ;
;
 ;
т.
;
т.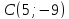 .
.
Найдём
координаты т.B:
в параллелограмме диагонали делят друг
друга пополам:
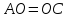 .
Найдём координаты т.
.
Найдём координаты т. :
т.
:
т.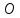 – середина
– середина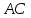 ,
следовательно, т.
,
следовательно, т.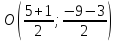 ;
т.
;
т.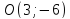 ,
но т.
,
но т.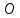 – середина
– середина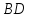 ,
следовательно,
,
следовательно,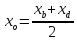 и
и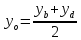 , поэтому
, поэтому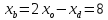 и
и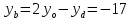 ,
т.
,
т.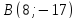 .
.
Ответ:
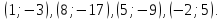
Задача №2:
Дана
прямая
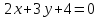 .
Составить уравнение прямой, проходящей
через точку
.
Составить уравнение прямой, проходящей
через точку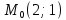 :
:
параллельно данной прямой.
перпендикулярно к данной прямой.
Решение:
Искомая прямая параллельна прямой
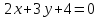 ,
поэтому её уравнение имеет вид:
,
поэтому её уравнение имеет вид: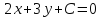 .
.
Найдём
т.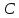 :
точка
:
точка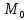 принадлежит этой прямой, поэтому её
координаты удовлетворяют записанному
уравнению:
принадлежит этой прямой, поэтому её
координаты удовлетворяют записанному
уравнению: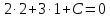 ,
,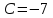 .
Итак, прямая принимает вид:
.
Итак, прямая принимает вид: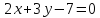 .
.
Т.к. заданная и искомые прямые перпендикулярны, то их угловые коэффициенты удовлетворяют условию:
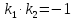 .
.
Найдём
угловой коэффициент прямой
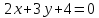 ;
;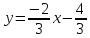 ;
итак,
;
итак,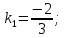 тогда
тогда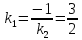 .
Запишем уравнение искомой прямой:
.
Запишем уравнение искомой прямой: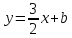 .
.
Точка
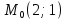 принадлежит этой прямой, поэтому
принадлежит этой прямой, поэтому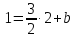 ;
;
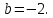 Уравнение
прямой принимает вид:
Уравнение
прямой принимает вид:
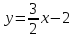
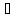
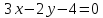 .
.
Ответ:
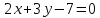 ;
;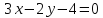 .
.
Задача №3:
Определить,
при каких значениях a
и b
две прямые
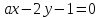 ,
,
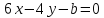 :
:
имеют одну общую точку;
параллельны;
совпадают.
Решение:
Прямые имеют одну общую точку, когда они не параллельны (их коэффициенты при x и y не пропорциональны):
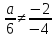 ;
;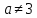
Прямые параллельны, когда коэффициенты при x и y пропорциональны:
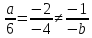 ;
;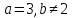 .
.Прямые совпадают, когда все их коэффициенты пропорциональны:
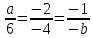 ;
;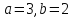 .
.
Задача №4:
Найти
проекцию точки
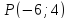 на прямую
на прямую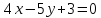 .
.
Решение:
Проведём
через т.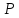 прямую
прямую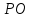 ,
перпендикулярную прямой
,
перпендикулярную прямой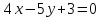 .
Точка
.
Точка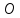 пересечения прямых и является искомой
проекцией.
пересечения прямых и является искомой
проекцией.
Прямая
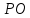 перпендикулярна заданной прямой, поэтому
её направляющим вектором служит
нормальный вектор прямой
перпендикулярна заданной прямой, поэтому
её направляющим вектором служит
нормальный вектор прямой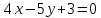 ,
т.е.
,
т.е.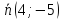 .
.
Запишем
уравнение прямой
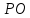 в каноническом виде:
в каноническом виде:
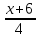
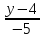 ;
;
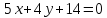 – уравнение
– уравнение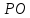 .
.
Найдём
координаты т.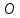 :
:
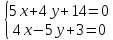 ;
;
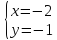 ;
т.
;
т.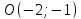
Ответ:
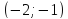
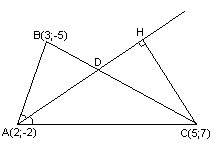
Задача №5:
Найти
точку
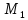 ,
симметричную точке
,
симметричную точке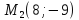 относительно прямой, проходящей через
точки
относительно прямой, проходящей через
точки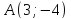 и
и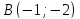 .
.
Решение:
Составим
уравнение
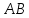 ,
как прямой проходящей через 2 точки:
,
как прямой проходящей через 2 точки:
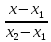
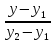 ;
;
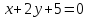 – уравнение
– уравнение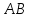 .
.
Найдём
уравнение прямой
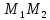 перпендикулярной
перпендикулярной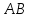 .
.
Нормальный
вектор
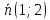 прямой
прямой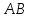 является направляющим вектором прямой
является направляющим вектором прямой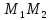 ,
поэтому используем каноническое
уравнение прямой:
,
поэтому используем каноническое
уравнение прямой: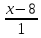
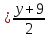 ;
;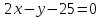 – уравнение прямой
– уравнение прямой .
.
Найдём
координат т. ,
как точки пересечения прямых
,
как точки пересечения прямых и
и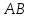 :
:
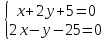 ;
;
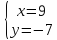 ;
т.
;
т.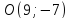 .
.
Так
как точка
 симметрична точке
симметрична точке относительно
относительно ,
следовательно
,
следовательно ,
то есть т.
,
то есть т.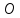 – середина отрезка
– середина отрезка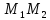 .
Найдём координаты точки
.
Найдём координаты точки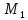 ,
зная начало и середину отрезка
,
зная начало и середину отрезка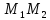 :
:
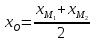 ,
,
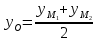 , тогда
, тогда
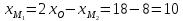 ,
,
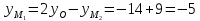 ,
,
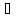 т.
т.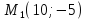 .
.
Ответ:
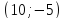 .
.
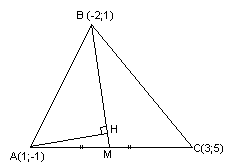
Задача №6:
Даны
вершины треугольника
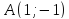 ,
,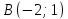 и
и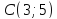 .
Составить уравнение перпендикуляра,
опущенного из вершины
.
Составить уравнение перпендикуляра,
опущенного из вершины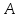 на медиану, проведенную из вершины
на медиану, проведенную из вершины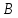 .
.
Решение:
Найдём
координаты т.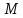 ,
как середины отрезка
,
как середины отрезка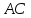 :
:
т.
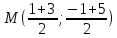 , т.
, т.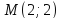 .
.
Запишем
уравнение медианы
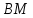 ,
как прямой, проходящей через две известные
точки:
,
как прямой, проходящей через две известные
точки:
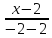
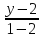 ;
;
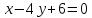 – уравнение
– уравнение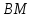 .
.
Нормальный
вектор для
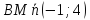 является направляющим для прямой
является направляющим для прямой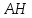 перпендикулярной
перпендикулярной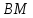 ,
тогда уравнение примет вид:
,
тогда уравнение примет вид:
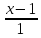
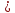
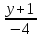 ;
;
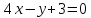 – уравнение
– уравнение .
.
Ответ:
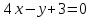 .
.
Задача №7:
Даны
вершины треугольника
 ,
,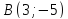 ,
,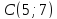 .
Составить уравнение перпендикуляра,
опущенного из вершины
.
Составить уравнение перпендикуляра,
опущенного из вершины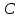 на биссектрису внутреннего угла при
вершине
на биссектрису внутреннего угла при
вершине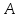 .
.
Решение:
Пусть
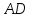 – биссектриса.
– биссектриса.
Найдём
координаты т.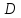 воспользовавшись свойством биссектрисы:
воспользовавшись свойством биссектрисы: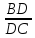
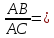
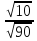
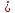
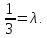 Тогда:
Тогда:
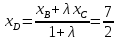 ;
;
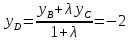 ;
т.
;
т.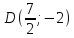 ;
;
Уравнение
биссектрисы
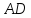 примет вид:
примет вид: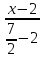 =
=
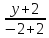 ⇒
⇒
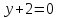 ,
,
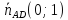 ,
,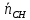 перпендикулярен
перпендикулярен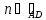 ⇒
⇒
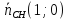 .
.
Точка
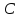 принадлежит искомому перпендикуляру,
поэтому уравнение
принадлежит искомому перпендикуляру,
поэтому уравнение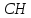 примет вид:
примет вид: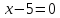 .
.
Ответ:
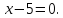
Задача №8:
Две
стороны квадрата лежат на прямых
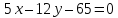 ,
,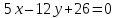 .
Вычислить его площадь.
.
Вычислить его площадь.
Решение:
Выберем на прямой
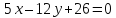 некоторую точку
некоторую точку :
:
пусть
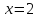 ,
тогда
,
тогда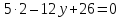 ⇒
⇒
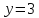 ,
т.е.
,
т.е.
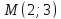 .
.
Найдём расстояние от точки
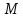 до прямой
до прямой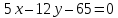 :
:
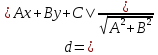 ⇒
⇒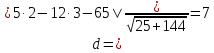 ,
где
,
где
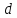 и есть длина стороны квадрата.
и есть длина стороны квадрата.
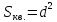 т.е.
т.е.
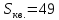 .
.
Ответ:
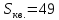 .
.
Задача №9:
Даны
две противоположные вершины квадрата
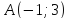 и
и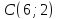 .
Составить уравнения его сторон.
.
Составить уравнения его сторон.
Решение:
Зная
вершины
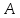 и
и составим уравнение диагонали
составим уравнение диагонали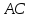 ,
как прямой проходящей через две точки:
,
как прямой проходящей через две точки: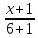
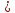
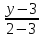 ⇒
⇒
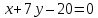 – уравнение прямой
– уравнение прямой
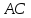 .
.
Т.к.
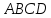 – квадрат, его диагонали являются
биссектрисами, поэтому
– квадрат, его диагонали являются
биссектрисами, поэтому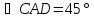 ;
найдём угловой коэффициент
;
найдём угловой коэффициент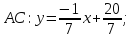
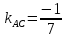 .
.
Зная
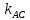 и
и ,
найдём угловой коэффициент
,
найдём угловой коэффициент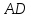 :
: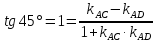 ;⇒
;⇒
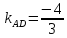 .
Уравнение
.
Уравнение
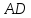 примет вид:
примет вид: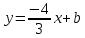 .
.
Найдём
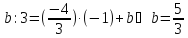 ;
Тогда уравнение
;
Тогда уравнение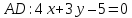 .
.
Т.к.
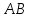 перпендикулярно
перпендикулярно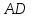 ⇒
угловой коэффициент
⇒
угловой коэффициент
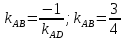 .
Уравнение
.
Уравнение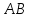 имеет вид:
имеет вид: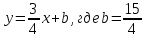 ,
тогда
,
тогда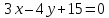 – уравнение
– уравнение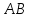 .
.
Т.к.
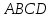 – квадрат, то
– квадрат, то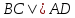 ,
то уравнение
,
то уравнение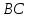 примет вид:
примет вид: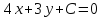 .
.
Зная,
что точка
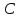 принадлежит прямой
принадлежит прямой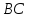 ,
найдём свободный член
,
найдём свободный член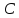 искомого уравнения, итак
искомого уравнения, итак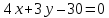 – уравнение стороны
– уравнение стороны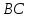 .
.
Аналогично
найдём уравнение стороны
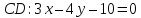 .
.
Ответ:
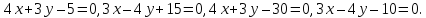
Задача №10:
Вычислить
площадь треугольника, отсекаемого
прямой
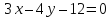 от координатного угла.
от координатного угла.
Решение:
Запишем
уравнение прямой
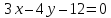 в отрезках:
в отрезках: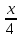 +
+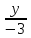
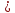 1.
1.
Из
этого уравнения следует, что длины
отрезков
 и
и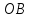 соответственно равны
соответственно равны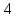 и
и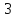 ,
поэтому
,
поэтому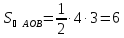 кв. ед.
кв. ед.
Ответ:
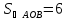 кв.ед.
кв.ед.
Задача №11:
Составить
уравнения сторон треугольника, зная
одну из его вершин
 и уравнения двух его медиан
и уравнения двух его медиан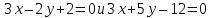 .
.
Решение:
Выясним,
что точка
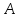 не принадлежит известным медианам
не принадлежит известным медианам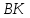 и
и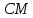 .
.
Найдём
координаты точки
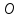 – пересечения медиан
– пересечения медиан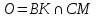 :
: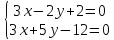 ⇒
т.
⇒
т.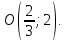
Продолжим
медиану
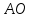 ,
и на её продолжении отложим отрезок
,
и на её продолжении отложим отрезок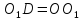 .
Соединим точку
.
Соединим точку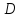 с вершинами
с вершинами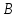 и
и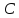 .
Полученный четырёхугольник
.
Полученный четырёхугольник – параллелограмм (его диагонали
пересекаясь в точке
– параллелограмм (его диагонали
пересекаясь в точке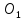 ,
делятся пополам).
,
делятся пополам).
Найдём
координаты точки
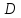 ,
как конца отрезка
,
как конца отрезка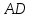 с известным началом
с известным началом и серединой
и серединой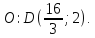
Найдём
уравнение прямой
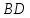 ,
зная, что
,
зная, что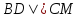 и точка
и точка лежит на этой прямой:
лежит на этой прямой: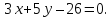
Найдём
координаты вершины
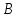 ,
как точки пересечения прямых
,
как точки пересечения прямых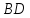 и
и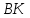 :
: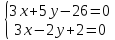 ⇒
т.
⇒
т.
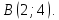
Точка
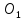 – середина отрезка
– середина отрезка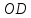 ,
поэтому
,
поэтому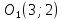 .
.
Найдём
координаты точки
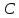 ,
как конца отрезка
,
как конца отрезка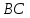 с известными началом
с известными началом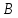 и серединой
и серединой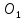 :
: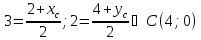 .
.
Зная
координаты всех вершин треугольника
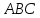 ,
найдём уравнения его сторон, как прямых
проходящих через две точки.
,
найдём уравнения его сторон, как прямых
проходящих через две точки.
Ответ:
Задача №12:
Составить
уравнения сторон треугольника, зная
одну из его вершин
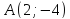 и уравнения биссектрис двух его углов:
и уравнения биссектрис двух его углов: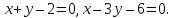
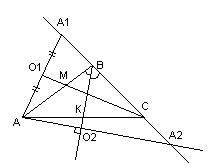
Решение:
Очевидно,
что точка
 не принадлежит заданным биссектрисам
не принадлежит заданным биссектрисам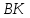 и
и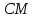 .
Найдём точку
.
Найдём точку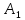 ,
симметричную точке
,
симметричную точке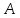 относительно биссектрисы
относительно биссектрисы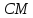 .
Можно доказать, что точка
.
Можно доказать, что точка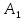 принадлежит прямой
принадлежит прямой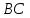 .
Опустим из т.
.
Опустим из т.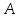 перпендикуляр на биссектрису
перпендикуляр на биссектрису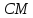 до пересечения в точке
до пересечения в точке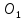 и отложим
и отложим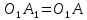 .
.
Т.к.
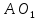 перпендикулярно
перпендикулярно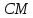 ,
то
,
то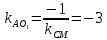 ;
точка
;
точка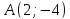 принадлежит прямой
принадлежит прямой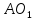 ,
поэтому её уравнение примет вид:
,
поэтому её уравнение примет вид: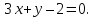
Координаты
точки
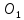 найдём как точки пересечения прямых
найдём как точки пересечения прямых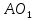 и
и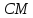 :
: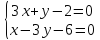 ⇒
т.
⇒
т.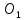 (
(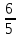 ;
;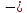
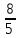 ).
).
Найдём
координаты точки
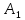 ,
как конца отрезка
,
как конца отрезка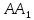 с известными началом
с известными началом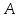 и серединой
и серединой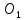 :
: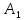 (
(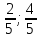 ).
).
Аналогично
найдём точку
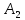 ,
симметричную т.
,
симметричную т.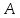 относительно биссектрисы
относительно биссектрисы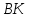 .
Точка
.
Точка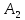 принадлежит прямой
принадлежит прямой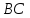 ,
,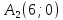 .
.
Тогда
уравнение стороны
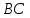 примет вид:
примет вид: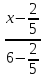
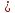
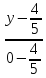 или
или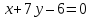 .
.
Найдём
координаты точек
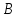 и
и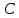 ,
как точек пересечения прямой
,
как точек пересечения прямой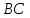 и заданных биссектрис:
и заданных биссектрис: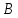 (
(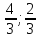 );
);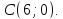
Зная
координаты вершин треугольника
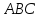 ,
найдём уравнения его сторон.
,
найдём уравнения его сторон.
Ответ:
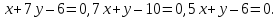
Задача №13:
Составить
уравнения биссектрис углов, образованных
двумя пересекающимися прямыми:
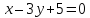 и
и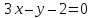 .
.
Решение:
Известно
свойство: биссектриса есть геометрическое
место точек, равноудалённых от сторон
угла.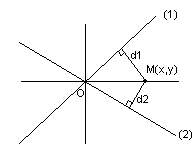
Пусть
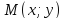 – произвольная точка искомой биссектрисы,
тогда
– произвольная точка искомой биссектрисы,
тогда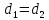 ;
;
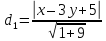 ;
;
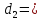
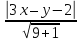 ;
;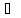
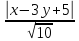
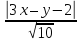 ;
;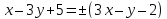 .
.
Тогда
уравнения биссектрис примут вид:
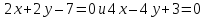 .
.
Ответ:
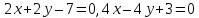 .
.
Задача №14:
Составить
уравнение биссектрисы угла между прямыми
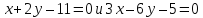 ,
в котором лежит точка
,
в котором лежит точка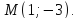
Решение:
Найдём
отклонение точки
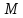 отзаданных
прямых, для этого приведём их уравнения
к нормальному виду:
отзаданных
прямых, для этого приведём их уравнения
к нормальному виду: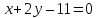 ;
нормирующий множитель
;
нормирующий множитель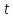
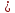 +
+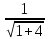
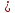
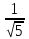 ;
;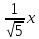 +
+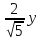
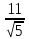
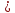 0.
0.
Найдём
отклонение
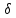 1
т.
1
т.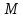 от прямой, для этого в левую часть
нормального уравнения подставим
координаты т.
от прямой, для этого в левую часть
нормального уравнения подставим
координаты т.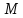 :
: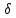 1
1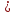
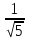 -
-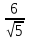 -
-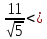 0.
0.
Аналогично
найдём отклонение
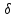 2
т.
2
т.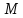 от второй прямой:
от второй прямой: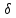 2
2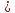 0.
Отклонения имеют разные знаки, поэтому
при раскрытии модулей (см. решение
предыдущей задачи) справа ставим знак
«минус».
0.
Отклонения имеют разные знаки, поэтому
при раскрытии модулей (см. решение
предыдущей задачи) справа ставим знак
«минус».
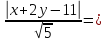
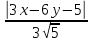 ⇒
⇒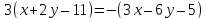
Уравнение
биссектрисы принимает вид:
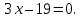
Ответ:
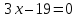 .
.
Задача №15:
На
прямой
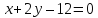 найти точки, равноудалённые от прямых
найти точки, равноудалённые от прямых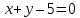 и
и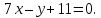
Решение:
Точки
равноудалённые от прямых
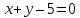 и
и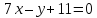 ,
лежат на биссектрисах углов, образованных
этими прямыми. Аналогично решению
предыдущих задач найдём их:
,
лежат на биссектрисах углов, образованных
этими прямыми. Аналогично решению
предыдущих задач найдём их: .
.
Тогда
искомые точки являются точками пересечения
этих биссектрис и прямой
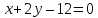 ,
поэтому найдём их, решая системы:
,
поэтому найдём их, решая системы: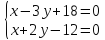 и
и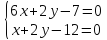 .
.
Ответ:
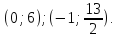
Задача №16:
Составить
уравнения сторон треугольника, зная
одну из его вершин
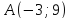 и уравнения медианы
и уравнения медианы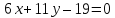 и высоты
и высоты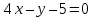 ,
проведённых из различных вершин.
,
проведённых из различных вершин.
Решение:
Убедимся,
что точка
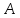 не принадлежит заданным медиане и
высоте.
не принадлежит заданным медиане и
высоте.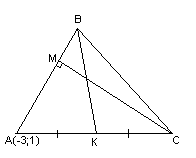
Найдём
уравнение стороны
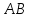 ,
зная, что
,
зная, что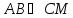 .
.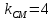 ⇒
⇒
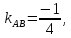 тогда уравнение примет вид:
тогда уравнение примет вид:
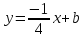 ,
зная координаты т.
,
зная координаты т. ,
принадлежащей
,
принадлежащей ,
найдём
,
найдём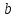 ,
тогда уравнение примет вид:
,
тогда уравнение примет вид: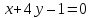 .
.
Найдём
координаты т.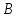 ,
как точки пересечения
,
как точки пересечения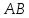 и
медианы
и
медианы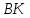 :
: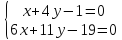 ⇒
⇒
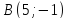 .
.
Пусть
точка
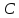 имеет координаты
имеет координаты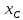 и
и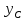 ,
найдём их. Точка
,
найдём их. Точка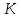 – середина
– середина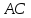 ,
поэтому
,
поэтому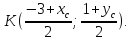
Точка
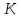 принадлежит медиане
принадлежит медиане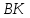 ,
точка
,
точка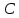 принадлежит высоте
принадлежит высоте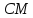 ,
поэтому
,
поэтому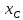 и
и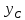 найдём, решая систему:
найдём, решая систему: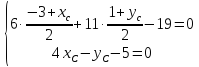
Откуда
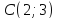 Зная координаты вершин треугольника,
найдём уравнения всех его сторон.
Зная координаты вершин треугольника,
найдём уравнения всех его сторон.
Ответ:
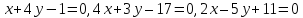 .
.
Задача №17:
Через
точку
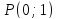 провести прямую так, чтобы её отрезок,
заключённый между прямыми
провести прямую так, чтобы её отрезок,
заключённый между прямыми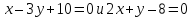 ,
делился бы в точке
,
делился бы в точке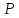 пополам.
пополам.
Решение:
Обозначим
через
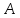 и
и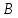 точки пересечения заданных прямых и
искомой прямой и пусть
точки пересечения заданных прямых и
искомой прямой и пусть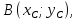 тогда
тогда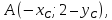 т.к.
т.к.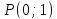 – середина отрезка
– середина отрезка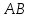 .
Координаты
.
Координаты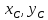 найдём, составив систему уравнений:
найдём, составив систему уравнений: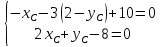 ⇒
⇒
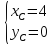 ⇒
⇒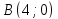 .
.
Составим
уравнение искомой прямой, которая
проходит через две точки, например,
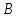 и
и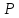 :
: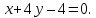
Ответ:
Задача
№18: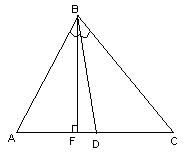
Составить
уравнения сторон треугольника
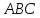 ,
зная одну из его вершин
,
зная одну из его вершин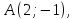 а также уравнение высоты
а также уравнение высоты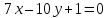 и биссектрисы
и биссектрисы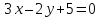 ,
проведённых из одной вершины. Решить
задачу, не вычисляя координат вершин
,
проведённых из одной вершины. Решить
задачу, не вычисляя координат вершин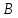 и
и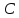 .
.
Решение:
Можно
проверить, что т.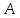 не принадлежит ни высоте,
ни биссектрисе.
Найдём уравнение стороны
не принадлежит ни высоте,
ни биссектрисе.
Найдём уравнение стороны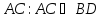 ,
поэтому
,
поэтому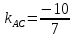 ;
;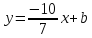 ,
зная координаты т.
,
зная координаты т. ,
найдём
,
найдём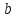 .
.
Итак,
уравнение
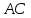 имеет вид:
имеет вид: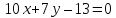 .
.
Рассмотрим
пучок с центром в т.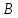 :
: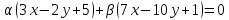 .
.
Пусть
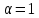 ,
тогда уравнение пучка примет вид:
,
тогда уравнение пучка примет вид:
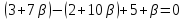 .
(1)
.
(1)
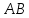 –прямая
пучка, причём координаты т.
–прямая
пучка, причём координаты т.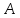 известны, поэтому найдём
известны, поэтому найдём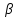 для прямой
для прямой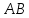 :
: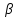
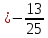 ,
поэтому уравнение
,
поэтому уравнение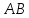 примет вид:
примет вид: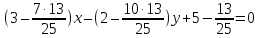 ,
т.е.
,
т.е.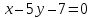 .
.
Найдём
угол между прямыми
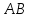 и
и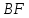 :tg
:tg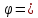
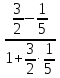
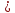 1⇒
1⇒
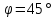 .
.
Тогда
угол
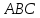 равен 90°, т.е.
равен 90°, т.е.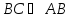 ;
-
;
-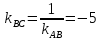 .
С другой стороны найдём
.
С другой стороны найдём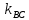 из уравнения (1):
из уравнения (1):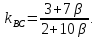
Итак,
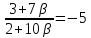 ⇒
⇒
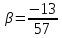 .
.
Найдём
уравнение стороны
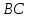 зная, что она принадлежит пучку. Подставим
зная, что она принадлежит пучку. Подставим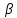 в уравнение (1) и получим уравнение
стороны
в уравнение (1) и получим уравнение
стороны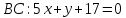 .
.
Ответ:
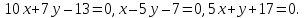
Образовательным результатом после изучения данной темы является сформированность компонент, заявленных во введении, совокупности компетенций (знать, уметь, владеть) на двух уровнях: пороговый и продвинутый. Пороговый уровень соответствует оценке «удовлетворительно», продвинутый уровень соответствует оценкам «хорошо» или «отлично» в зависимости от результатов защиты кейс-заданий.
Для самостоятельной диагностики данных компонент вам предлагаются следующие задания.
