
- •Аналитическая геометрия
- •§1 Векторы………………………………………………………………..8
- •§1 Векторы.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №1.
- •§2 Прямая на плоскости.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №2.
- •§3 Прямая и плоскость в пространстве.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №3.
- •§4 Кривые 2-го порядка.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №4.
- •Аналитическая геометрия практикум по решению задач
- •426034, Ижевск, Университетская, д. 1, корп. 4, каб. 207
§3 Прямая и плоскость в пространстве.
ПЛОСКОСТЬ.
Определение.
Любой ненулевой вектор, перпендикулярный
плоскости, называется её нормальным
вектором,
и обозначается
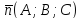 .
.
Определение.
Уравнение плоскости вида
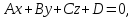 где коэффициенты
где коэффициенты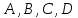 – произвольные действительные числа,
одновременно не равные нулю, называетсяобщим
уравнением плоскости.
– произвольные действительные числа,
одновременно не равные нулю, называетсяобщим
уравнением плоскости.
Теорема.
Уравнение
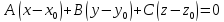 определяет плоскость, проходящую через
точку
определяет плоскость, проходящую через
точку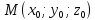 и имеющую нормальный вектор
и имеющую нормальный вектор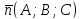 .
.
Определение.
Уравнение плоскости вида
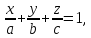 где
где
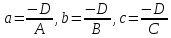 – произвольные, не равные нулю
действительные числа, называетсяуравнением
плоскости в отрезках.
– произвольные, не равные нулю
действительные числа, называетсяуравнением
плоскости в отрезках.
Теорема.
Пусть
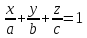 – уравнение плоскости в отрезках. Тогда
– уравнение плоскости в отрезках. Тогда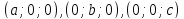 – координаты точек её пересечения с
осями координат.
– координаты точек её пересечения с
осями координат.
Определение.
Общее уравнение плоскости
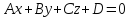 называетсянормированным
или
нормальным
уравнением плоскости, если
называетсянормированным
или
нормальным
уравнением плоскости, если
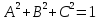 и
и
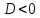 .
.
Теорема.
Нормальное уравнение плоскости может
быть записано в виде
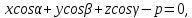 где
где
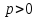 – расстояние от начала координат до
данной плоскости,
– расстояние от начала координат до
данной плоскости,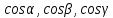 – направляющие косинусы её нормального
вектора
– направляющие косинусы её нормального
вектора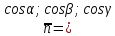 ).
).
Определение.
Нормирующим
множителем
общего уравнения плоскости
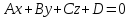 называется
число
называется
число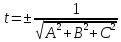 – где знак выбирается противоположным
знаку свободного членаD.
– где знак выбирается противоположным
знаку свободного членаD.
Теорема.
Пусть
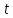 – нормирующий множитель общего уравнения
плоскости
– нормирующий множитель общего уравнения
плоскости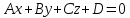 .
Тогда уравнение
.
Тогда уравнение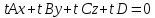 – является нормированным уравнением
данной плоскости.
– является нормированным уравнением
данной плоскости.
Теорема.
Расстояние d
от точки
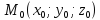 до плоскости
до плоскости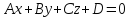 равно
равно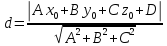 .
.
Взаимное расположение двух плоскостей.
Две плоскости либо совпадают, либо являются параллельными, либо пересекаются по прямой.
Теорема.
Пусть плоскости заданы общими уравнениями:
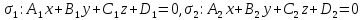 .
Тогда:
.
Тогда:
1)
если
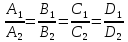 ,
то плоскости совпадают;
,
то плоскости совпадают;
2)
если
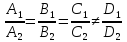 ,
то плоскости параллельные;
,
то плоскости параллельные;
3)
если
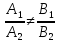 или
или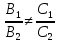 ,
то
плоскости пересекаются по прямой,
уравнением которой служит система
уравнений:
,
то
плоскости пересекаются по прямой,
уравнением которой служит система
уравнений:
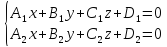 .
.
Теорема.
Пусть
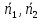 – нормальные векторы двух плоскостей,
тогда один из двух углов между данными
плоскостями равен:
– нормальные векторы двух плоскостей,
тогда один из двух углов между данными
плоскостями равен: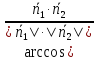 .
.
Следствие.
Пусть
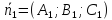 ,
,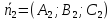 – нормальные векторы двух данных
плоскостей. Если скалярное произведение
– нормальные векторы двух данных
плоскостей. Если скалярное произведение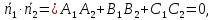 то данные плоскости являются
перпендикулярными.
то данные плоскости являются
перпендикулярными.
Теорема.
Пусть даны координаты трех различных
точек координатного пространства:
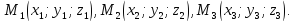
Тогда
уравнение
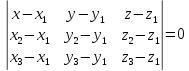 –является
уравнением плоскости, проходящей через
эти три точки.
–является
уравнением плоскости, проходящей через
эти три точки.
Теорема.
Пусть даны общие уравнения двух
пересекающихся плоскостей:
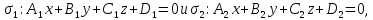 причем
причем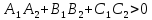 .
Тогда:
.
Тогда:
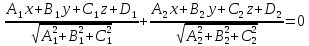 .
.
– уравнение биссекторной плоскости острого двугранного угла, образованного пересечением данных плоскостей;
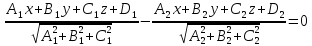 .
.
– уравнение биссекторной плоскости тупого двугранного угла.
Связка и пучок плоскостей.
Определение. Связкой плоскостей называется множество всех плоскостей, имеющих одну общую точку, которая называется центром связки.
Теорема.
Пусть
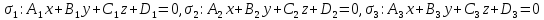 – три плоскости, имеющие единственную
общую точку
– три плоскости, имеющие единственную
общую точку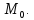 Тогда уравнение
Тогда уравнение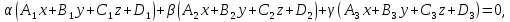 где
где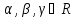 – произвольные действительные параметры
одновременно не равные нулю, естьуравнение
связки плоскостей.
– произвольные действительные параметры
одновременно не равные нулю, естьуравнение
связки плоскостей.
Теорема.
Уравнение
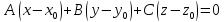 ,
где
,
где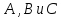 произвольные действительные параметры,
одновременно не равные нулю, являетсяуравнением
связки плоскостей с центром связки
в точке
произвольные действительные параметры,
одновременно не равные нулю, являетсяуравнением
связки плоскостей с центром связки
в точке
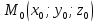 .
.
Теорема. Пусть даны общие уравнения трех плоскостей:
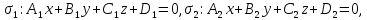
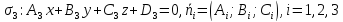 –их
соответствующие нормальные векторы.
Для того чтобы три данные плоскости
пересекались в единственной точке
необходимо и достаточно, чтобы смешанное
произведение их нормальных векторов
не равнялось нулю:
–их
соответствующие нормальные векторы.
Для того чтобы три данные плоскости
пересекались в единственной точке
необходимо и достаточно, чтобы смешанное
произведение их нормальных векторов
не равнялось нулю:
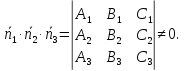
В
этом случае, координаты их единственной
общей точки являются единственным
решением системы уравнений:
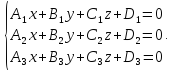
Определение. Пучком плоскостей называется множество всех плоскостей пересекающихся по одной и той же прямой, называемой осью пучка.
Теорема.
Пусть
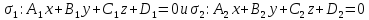 – две плоскости, пересекающиеся по
прямой
– две плоскости, пересекающиеся по
прямой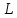 .
Тогда уравнение
.
Тогда уравнение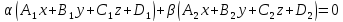 ,
где
,
где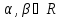 – произвольные действительные параметры
одновременно не равные нулю, естьуравнение
пучка плоскостей
с осью пучка
– произвольные действительные параметры
одновременно не равные нулю, естьуравнение
пучка плоскостей
с осью пучка

ПРЯМАЯ.
Определение.
Любой ненулевой вектор, коллинеарный
данной прямой называется ее направляющим
вектором,
и обозначается
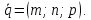
Теорема.
Следующая система уравнений является
уравнением прямой в пространстве и
называется параметрическим
уравнением прямой
в пространстве:
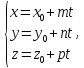 где
где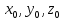 – координаты произвольной фиксированной
точки данной прямой,
– координаты произвольной фиксированной
точки данной прямой,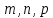 – соответствующие координаты произвольного
направляющего вектора данной прямой,
– соответствующие координаты произвольного
направляющего вектора данной прямой,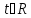 – параметр.
– параметр.
Следствие.
Следующая система уравнений является
уравнением прямой в пространстве и
называется каноническим
уравнением прямой
в пространстве:
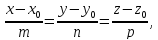 где
где
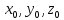 – координаты произвольной фиксированной
точки данной прямой,
– координаты произвольной фиксированной
точки данной прямой,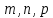 – соответствующие координаты произвольного
направляющего вектора данной прямой.
– соответствующие координаты произвольного
направляющего вектора данной прямой.
Определение.
Каноническое уравнение прямой
вида
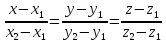 – называетсяканоническим
уравнением прямой, проходящей через
две различные данные точки
– называетсяканоническим
уравнением прямой, проходящей через
две различные данные точки
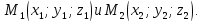
Взаимное расположение двух прямых в пространстве.
Возможны 4 случая расположения двух прямых в пространстве. Прямые могут совпадать, быть параллельными, пересекаться в одной точке или быть скрещивающимися.
Теорема. Пусть даны канонические уравнения двух прямых:
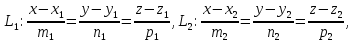
где
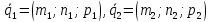 – их направляющие векторы,
– их направляющие векторы,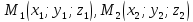 – произвольные фиксированные точки,
лежащие на прямых
– произвольные фиксированные точки,
лежащие на прямых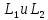 соответственно. Тогда:
соответственно. Тогда:
прямые совпадают, если
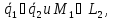 т.е.
т.е.
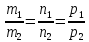 и
и
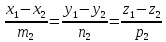 ;
;
прямые параллельные, если
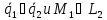 ,
т.е.
,
т.е.
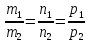 и
не выполняется хотя бы одно из равенств
и
не выполняется хотя бы одно из равенств
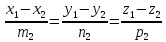 ;
;
прямые пересекаются в одной точке, если
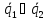 ,
т.е. хотя бы одно из равенств
,
т.е. хотя бы одно из равенств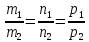 не выполняется и
не выполняется и
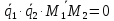 ,
т.е.
,
т.е.
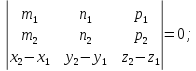
4)
прямые скрещивающиеся, если
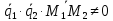 ,
т.е.
,
т.е.
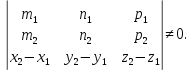
Теорема.
Пусть
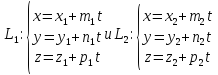
– две произвольные прямые в пространстве, заданные параметрическими уравнениями. Тогда:
1)
если система уравнений
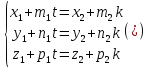
имеет
единственное решение
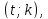 то прямые пересекаются в одной точке;
то прямые пересекаются в одной точке;
2)
если система уравнений
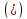 не имеет решений, то прямые скрещивающиеся
или параллельные.
не имеет решений, то прямые скрещивающиеся
или параллельные.
3)
если система уравнений
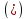 имеет более одного решения, то прямые
совпадают.
имеет более одного решения, то прямые
совпадают.
Расстояние между двумя прямыми в пространстве.
Теорема. (Формула расстояния между двумя параллельными прямыми.): Расстояние между двумя параллельными прямыми
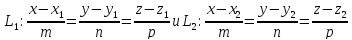 ,
где
,
где
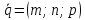 – их общий направляющий вектор,
– их общий направляющий вектор,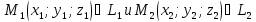 – точки на этих прямых, можно вычислить
по формуле:
– точки на этих прямых, можно вычислить
по формуле:
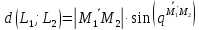 или
или
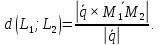

Теорема. (Формула расстояния между двумя скрещивающимися прямыми.): Расстояние между двумя скрещивающимися прямыми
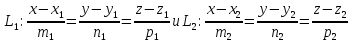
можно
вычислить по формуле:
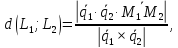
где
 – модуль смешанного произведения
направляющих векторов
– модуль смешанного произведения
направляющих векторов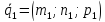 и
и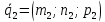 и вектора
и вектора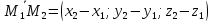 ,
,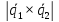 – модуль векторного произведения
направляющих векторов.
– модуль векторного произведения
направляющих векторов.
Теорема.
Пусть
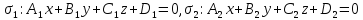 –
уравнения двух пересекающихся плоскостей.
Тогда следующая система уравнений
является уравнением прямой линии, по
которой пересекаются эти плоскости:
–
уравнения двух пересекающихся плоскостей.
Тогда следующая система уравнений
является уравнением прямой линии, по
которой пересекаются эти плоскости: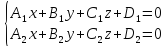 .
Направляющим вектором этой прямой
может служить вектор
.
Направляющим вектором этой прямой
может служить вектор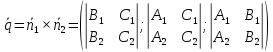 ,
где
,
где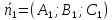 ,
,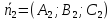 – нормальные векторы данных плоскостей.
– нормальные векторы данных плоскостей.
Теорема.
Пусть дано каноническое уравнение
прямой:
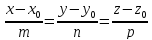 ,
где
,
где
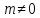 .
Тогда следующая система уравнений
является уравнением данной прямой,
заданной пересечением двух плоскостей:
.
Тогда следующая система уравнений
является уравнением данной прямой,
заданной пересечением двух плоскостей: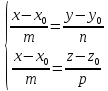 .
.
Теорема.
Уравнение перпендикуляра, опущенного
из точки
 на прямую
на прямую
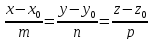 имеет вид
имеет вид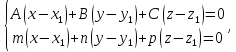 где
где
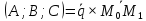 – координаты векторного произведения,
– координаты векторного произведения,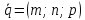 – координаты направляющего вектора
данной прямой. Длину перпендикуляра
можно найти по формуле:
– координаты направляющего вектора
данной прямой. Длину перпендикуляра
можно найти по формуле: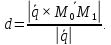
Теорема.
Уравнение общего перпендикуляра двух
скрещивающихся прямых
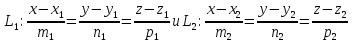 имеет вид:
имеет вид:
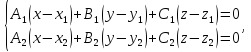 где
где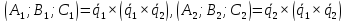 .
.
Взаимное расположение прямой и плоскости в пространстве.
Возможны три случая взаимного расположения прямой в пространстве и плоскости:
1) прямая лежит на плоскости;
2) прямая параллельна плоскости;
3) прямая пересекает плоскость в некоторой точке.
Теорема.
Пусть плоскость
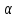 задана общим уравнением
задана общим уравнением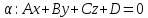 ,
а
прямая
,
а
прямая
 задана каноническим или параметрическим
уравнениями
задана каноническим или параметрическим
уравнениями или
или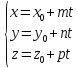 ,
где
вектор
,
где
вектор
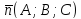 – нормальный вектор плоскости
– нормальный вектор плоскости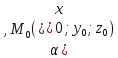 – координаты произвольной фиксированной
точки прямой
– координаты произвольной фиксированной
точки прямой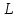 ,
,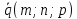 – соответствующие координаты произвольного
направляющего вектора прямой
– соответствующие координаты произвольного
направляющего вектора прямой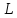 .
Тогда:
.
Тогда:
1)
если
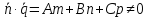 ,
то прямая
,
то прямая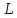 пересекает плоскость
пересекает плоскость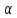 в точке, координаты которой можно найти
из системы уравнений
в точке, координаты которой можно найти
из системы уравнений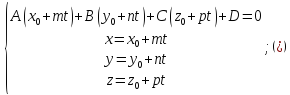
2)
если
 и
и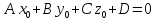 ,
то прямая лежит на плоскости;
,
то прямая лежит на плоскости;
3)
если
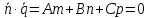 и
и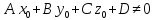 ,
то прямая параллельна плоскости.
,
то прямая параллельна плоскости.
Следствие. Если система (*) имеет единственное решение, то прямая пересекается с плоскостью; если система (*) не имеет решений, то прямая параллельная плоскости; если система (*) имеет бесконечно много решений, то прямая лежит на плоскости.
Решение типовых задач.
Задача №1:
Составить
уравнение плоскости, проходящей через
точку
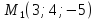 параллельно
векторам
параллельно
векторам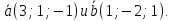
Решение:
Найдём
нормальный вектор искомой плоскости:
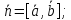
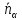 =
=
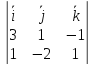 =
=
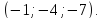
В
качестве нормального вектора плоскости
можно взять вектор
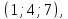 тогда общее уравнение плоскости примет
вид:
тогда общее уравнение плоскости примет
вид:
Чтобы
найти
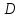 ,
нужно заменить в этом уравнении
,
нужно заменить в этом уравнении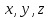 координатами точки
координатами точки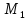 ,
принадлежащей плоскости
,
принадлежащей плоскости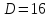 .
.
Ответ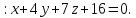
Задача №2:
Две
грани куба лежат на плоскостях
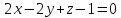 и
и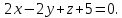 Вычислить объём этого куба.
Вычислить объём этого куба.
Решение:
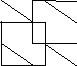
Очевидно,
что плоскости параллельны. Длиной ребра
 куба является расстояние между
плоскостями. Выберем на первой плоскости
произвольную точку
куба является расстояние между
плоскостями. Выберем на первой плоскости
произвольную точку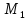 :
пусть
:
пусть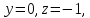 найдём
найдём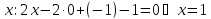 .
.
Итак,
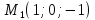 .
.
Найдём
расстояние между плоскостями как
расстояние от точки
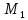 до второй плоскости:
до второй плоскости:
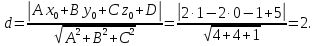
Итак,
объём куба равен
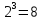 (
(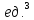 )
)
Ответ:
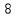 .
.

Задача №3:
Найти
угол между гранями
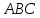 и
и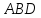 пирамиды
пирамиды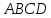 c
вершинами
c
вершинами
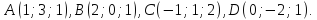
Решение:
Угол
между плоскостями
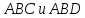 – это угол между нормальными векторами
к этим плоскостям. Найдём нормальный
вектор
– это угол между нормальными векторами
к этим плоскостям. Найдём нормальный
вектор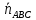 плоскости
плоскости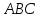 :
: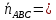 [
[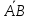 ,
,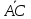 ];
];
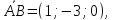
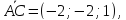
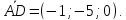
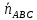
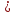

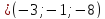 ,
или
,
или
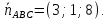
Аналогично
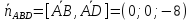
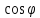
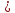
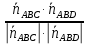
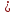
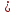
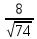 .
.
Ответ:
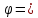
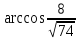 .
.
Задача №4:
Составить
каноническое уравнение прямой
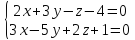 .
.
Решение:
Найдём произвольную точку
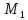 прямой, для этого решим систему. Пусть
прямой, для этого решим систему. Пусть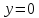 ,
тогда
,
тогда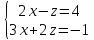 , откуда
, откуда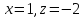 .
.
Итак,
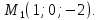
Найдём направляющий вектор
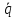 прямой.
прямой.
Вектор
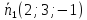 и
и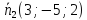 перпендикулярны прямой, поэтому
перпендикулярны прямой, поэтому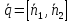 ,
,
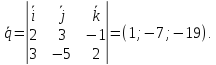
Итак,
каноническое уравнение прямой примет
вид

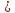
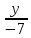
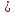
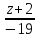 .
.
Ответ:
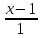
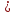
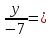
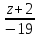 .
.
Задача №5:
Найти расстояние между прямыми
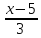
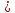
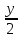
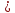
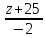 и
и
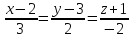 .
.
Решение:
Прямые
параллельны, т.к. их направляющие векторы
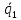 и
и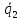 равны. Пусть точка
равны. Пусть точка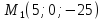 принадлежит первой прямой,a
точка
принадлежит первой прямой,a
точка
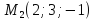 лежит на второй прямой. Найдём площадь
параллелограмма, построенного на
векторах
лежит на второй прямой. Найдём площадь
параллелограмма, построенного на
векторах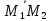 и
и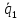 .
.
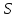
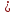
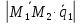 ;
;
[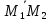 ,
,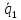 ]
]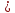
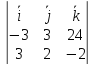
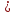
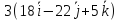 ;
;
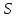
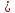 3∙
3∙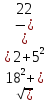 21∙
21∙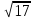 (ед.3).
(ед.3).
Далее найдём длину основание параллелограмма:
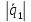
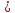
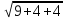
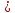
 .
.
Искомым
расстоянием является высота параллелограмма,
опущенная из точки
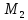 :
:
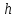
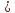
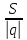
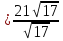
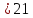 ед.
ед.
Ответ:
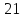 .
.
Задача №6:
Вычислить кратчайшее расстояние между прямыми:
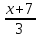

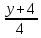
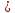
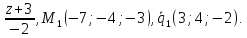
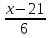
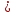
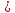
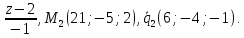
Покажем,
что прямые скрещивающиеся, т.е. векторы
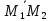 ,
,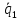 и
и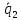 не принадлежат одной плоскости:
не принадлежат одной плоскости: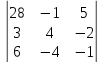 ≠ 0.
≠ 0.
1 способ:
Через
вторую прямую проведём плоскость
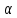 ,
параллельную первой прямой. Для искомой
плоскости известны принадлежащие ей
векторы
,
параллельную первой прямой. Для искомой
плоскости известны принадлежащие ей
векторы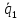 и
и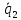 и точка
и точка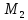 .
Нормальный вектор
.
Нормальный вектор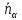 плоскости
плоскости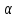 есть векторное произведение векторов
есть векторное произведение векторов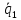 и
и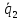 ,
поэтому
,
поэтому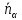
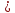
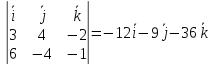 .
.
Итак,
в качестве нормального вектора плоскости
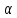 можно взять вектор
можно взять вектор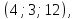 поэтому уравнение плоскости примет
вид:
поэтому уравнение плоскости примет
вид: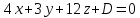 зная, что точка
зная, что точка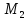 принадлежит плоскости
принадлежит плоскости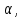 найдём
найдём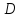 и запишем уравнение:
и запишем уравнение: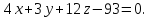
Искомое
расстояние – это расстояние от точки
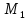 первой прямой до плоскости
первой прямой до плоскости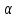 и находится по формуле:
и находится по формуле:
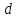

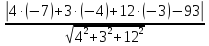
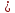 13.
13.
2 способ:
На
векторах
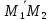 ,
,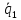 и
и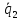 построим параллелепипед.
построим параллелепипед.
Искомое
расстояние – это высота параллелепипеда,
опущенная из точки
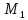 ,
на его основание, построенного на
векторах
,
на его основание, построенного на
векторах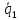 и
и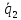 .
.
Ответ: 13 единиц.
Задача №7:
Найти
проекцию точки
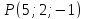 на плоскость
на плоскость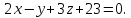
Решение:
Через точку
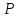 проведём прямую, перпендикулярную
плоскости.
проведём прямую, перпендикулярную
плоскости.Найдём точку
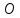 пересечения прямой и плоскости. Точка
пересечения прямой и плоскости. Точка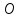 –
проекция точки
–
проекция точки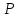 на плоскость.
на плоскость.
 Нормальный
вектор
Нормальный
вектор
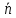 плоскости является направляющий вектором
прямой:
плоскости является направляющий вектором
прямой:
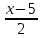
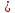
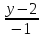
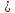
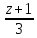 или
или
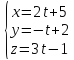 .
.
Найдём
точку
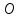 пересечения прямой
пересечения прямой
и плоскости:
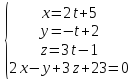 .
.
Подставив
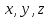 в уравнение плоскости, найдём
в уравнение плоскости, найдём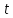 ,
а затем
,
а затем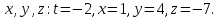
Ответ:
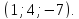
Замечание.
Чтобы найти точку
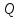 ,
симметричную точке
,
симметричную точке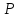 относительно плоскости, нужно (аналогично
предыдущей задаче) найти проекцию
относительно плоскости, нужно (аналогично
предыдущей задаче) найти проекцию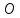 точки
точки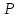 на плоскость, затем рассмотреть отрезок
на плоскость, затем рассмотреть отрезок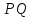 с известными началом
с известными началом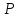 и серединой
и серединой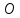 ,
воспользовавшись формулами
,
воспользовавшись формулами ,
,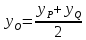 ,
,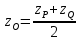 .
.
Задача №8:
Найти
уравнение перпендикуляра, опущенного
из точки
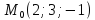 на прямую
на прямую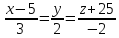 .
.
Решение:
1 способ:
Проведём плоскость
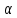 через точку
через точку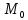 и заданную прямую.
и заданную прямую.Проведём плоскость
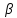 через точку
через точку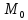 перпендикулярно прямой.
перпендикулярно прямой.Искомый перпендикуляр есть пересечение плоскостей
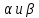 .
.
2 способ:
Проведём плоскость
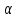 через точку
через точку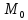 ,
перпендикулярно прямой.
,
перпендикулярно прямой.Найдём точку
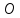 пересечения плоскости
пересечения плоскости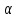 и прямой.
и прямой.Уравнение искомого перпендикуляра – это уравнение прямой, проходящей через точки
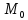 и
и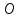 .
.
Задачу решим вторым способом:
Плоскость
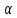 перпендикулярна заданной прямой, поэтому
направляющий вектор прямой является
нормальным вектором плоскости. Зная
нормальный вектор плоскости и точку на
плоскости, запишем её уравнение:
перпендикулярна заданной прямой, поэтому
направляющий вектор прямой является
нормальным вектором плоскости. Зная
нормальный вектор плоскости и точку на
плоскости, запишем её уравнение: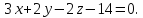
Найдём
точку
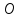 пересечения плоскости и прямой, записанной
параметрически:
пересечения плоскости и прямой, записанной
параметрически:
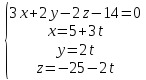 ,
,
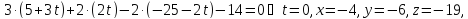 итак,
итак,
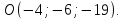
Составим
уравнение прямой проходящей через точки
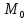 и
и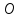 :
:
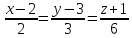 .
.
Ответ:
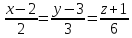 .
.
Таким же способом можно решить и следующие задачи:
Найти расстояние от точки до прямой. (Для предыдущей задачи ответом будет расстояние
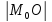 ).
).Найти проекцию точки на прямую (точка
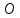 – проекция точки
– проекция точки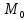 ).
).Найти точку, симметричную точке относительно прямой.
Задача №9:
Найти
точку
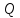 ,
симметричную точке
,
симметричную точке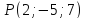 относительно прямой
относительно прямой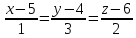 .
.
Решение:
Проведём плоскость через точку
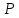 перпендикулярно заданной прямой:
перпендикулярно заданной прямой: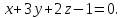
Найдём точку
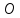 пересечения прямой и плоскости
пересечения прямой и плоскости
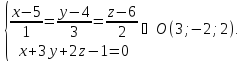
Найдём координаты точки
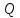 как конца отрезка
как конца отрезка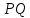 с известными началом
с известными началом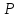 и серединой
и серединой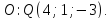
Ответ:
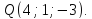
Задача №10:
Дан
треугольник
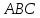 с вершинами
с вершинами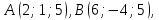
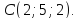 Найти, уравнение высоты, опущенной из
вершины
Найти, уравнение высоты, опущенной из
вершины
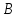 на сторону
на сторону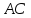 .
.
Решение:
Ход решения совершенно аналогичен предыдущим задачам.
Ответ:
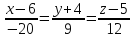 .
.
Задача №11:
Найти
уравнение общего перпендикуляра к двум
прямым:
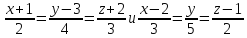 .
.
Решение:
Докажем, что прямые являются скрещивающимися, для этого составим определитель, строками которого являются координаты векторов
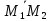 ,
,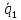 ,
,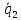 :
:
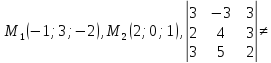 0.
0.
Найдём уравнение плоскости
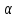 ,
проходящей через первую прямую
параллельно второй прямой
,
проходящей через первую прямую
параллельно второй прямой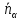

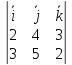
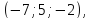 (
(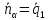 ∙
∙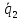 ).
).
Учитывая,
что плоскость
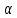 проходит через точку
проходит через точку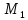 ,
запишем уравнение этой плоскости:
,
запишем уравнение этой плоскости: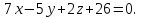
Найдём уравнение плоскости
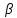 ,
перпендикулярной плоскости
,
перпендикулярной плоскости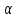 и
проходящей через первую прямую:
и
проходящей через первую прямую: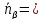
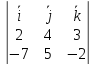
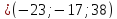 ,
,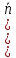 ∙
∙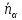 ).
).
Точка
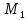 принадлежит
принадлежит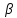 ,
поэтому уравнение плоскости
,
поэтому уравнение плоскости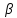 примет вид:
примет вид: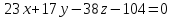 .
.
Аналогично, найдём уравнение плоскости
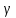 ,
перпендикулярной плоскости
,
перпендикулярной плоскости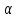 и проходящей через вторую прямую:
и проходящей через вторую прямую: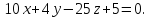
Уравнением общего перпендикуляра к заданным прямым является уравнение линии пересечения плоскостей:
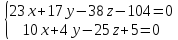 .
.
Ответ:
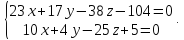
Задача №12:
Составить
уравнение прямой проходящей через точку
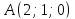 и пересекающей прямые
и пересекающей прямые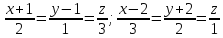 .
.
Решение:
Первая
прямая проходит через точку
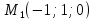 и имеет направляющий вектор
и имеет направляющий вектор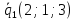 ;
вторая – проходит через точку
;
вторая – проходит через точку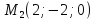 и имеет направляющий вектор
и имеет направляющий вектор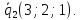
Покажем,
что эти прямые являются скрещивающимися,
для этого составим определитель, строки
которого являются координатами векторов
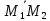 ,
,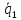 ,
, ,
,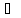 векторы не принадлежат одной плоскости.
векторы не принадлежат одной плоскости.
Проведём
плоскость
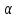 через точку
через точку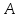 и первую прямую:
и первую прямую: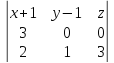
Пусть
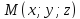 – произвольная точка плоскости
– произвольная точка плоскости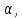 тогда векторы
тогда векторы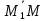 ,
,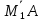 и
и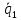 компланарны. Уравнение плоскости
компланарны. Уравнение плоскости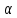 имеет вид:
имеет вид: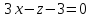 .
.
Аналогично
составим уравнение плоскости
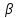 ,
проходящей через точку
,
проходящей через точку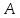 и вторую прямую:
и вторую прямую: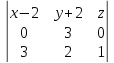
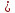 0
0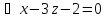 .
.
Искомая
прямая есть пересечение плоскостей
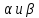 ,
т.е.
,
т.е.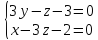 .
.
Ответ: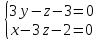 .
.
Образовательным результатом после изучения данной темы является сформированность компонент, заявленных во введении, совокупности компетенций (знать, уметь, владеть) на двух уровнях: пороговый и продвинутый. Пороговый уровень соответствует оценке «удовлетворительно», продвинутый уровень соответствует оценкам «хорошо» или «отлично» в зависимости от результатов защиты кейс-заданий.
Для самостоятельной диагностики данных компонент вам предлагаются следующие задания.
