16. Геометрическое распределение

Геометри́ческое распределе́ние в теории вероятностей — распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».

Определение

Пусть — бесконечная последовательность независимых случайных величин с распределением Бернулли, то есть

Построим случайную величину — количество «неудач» до первого «успеха». Распределение случайной величины Y называется геометрическим с вероятностью «успеха» P , что обозначается следующим образом: .

Функция вероятности случайной величины имеет вид:

17. Биноминальное распределение

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна p

Определение

Пусть  — конечная последовательность независимых случайных величин с распределением Бернулли, то есть

Построим случайную величину :

.

Тогда , число единиц (успехов) в последовательности , имеет биномиальное распределение с степенями свободы и вероятностью «успеха» . Пишем: . Её функция плотности вероятности задаётся формулой:

где  — биномиальный коэффициент.

18. Распределение Пуассона. Элементы теории массового обсл. Простой поток.

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Распределение Пуассона играет ключевую роль в теории массового обслуживания.

Определение

Выберем фиксированное число  и определим дискретное распределение, задаваемое следующей функцией вероятности:

,

где

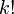•  обозначает факториал,

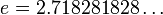•  — основание натурального логарифма.

Тот факт, что случайная величина  имеет распределение Пуассона с параметром , записывается: .

Простейший поток

Однородный стационарный поток без последействий является простейшим, потоком Пуассона.

Число  событий такого потока, выпадающих на интервал , распределено по Закону Пуассона:

Пуассоновский поток заявок удобен при решении задач ТМО. Строго говоря простейшие потоки редки на практике, однако

многие моделируемые потоки допустимо рассматривать как простейшие.

19. –

20. Плотность вероятности непрерывной случайной величины. Кривая распределения. Элемент вероятности.

Пло́тность вероя́тности — один из способов задания вероятностной меры на евклидовом пространстве . В случае когда вероятностная мера является распределением случайной величины, говорят о плотности случайной величины.

Плотность вероятности

Пусть  является вероятностной мерой на , то есть определено вероятностное пространство , где  обозначает борелевскую σ-алгебру на . Пусть обозначает меру Лебега на .

Определение 1. Вероятность  называется абсолютно непрерывной (относительно меры Лебега) (), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

Если вероятность  абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция  такая, что

,

где использовано общепринятое сокращение , и интеграл понимается в смысле Лебега.

Определение 2. В более общем виде, пусть  — произвольное измеримое пространство, а  и  — две меры на этом пространстве. Если найдется неотрицательная , позволяющая выразить меру  через меру  в виде

то такую функцию называют плотностью меры  по мере , или производной Радона-Никодима меры  относительно меры , и обозначают

21. Сво-ва пл вер.

Свойства плотности вероятности

• Плотность вероятности определена почти всюду. Если  является плотностью вероятности  и  почти всюду относительно меры Лебега, то и функция  также является плотностью вероятности .

• Интеграл от плотности по всему пространству равен единице:

.

Обратно, если  — неотрицательная п.в. функция, такая что , то существует абсолютно непрерывная вероятностная мера  на  такая, что  является её плотностью.

• Замена меры в интеграле Лебега:

,

где  любая борелевская функция, интегрируемая относительно вероятностной меры .