Задание №3 для контрольной работы*.

Найти:

а) частное решение линейного неоднородного уравнения 2-го порядка;

б) общее решение линейного неоднородного дифференциального уравнения.

3.1. а) б)
3.2. а) б)
3.3. а) б)
3.4. а) б)
3.5. а) б)
3.6. а) б)
3.7. а) б)
3.8. а) б)
3.9. а) б)
3.10. а) б)
3.11. а) б)
3.12. а) б)
3.13. а) б)
3.14. а) б)
3.15. а) б)
3.16. а) б)
3.17. а) б)
3.18. а) б)
3.19. а) б)
3.20. а) б)
3.21. а) б)
3.22. а) б)
3.23. а) б)
3.24. а) б)

III. Система линейных дифференциальных уравнений 1-го порядка с постоянными коэффициентами.

Рассмотрим метод исключения. Дана система линейных дифференциальных уравнений:

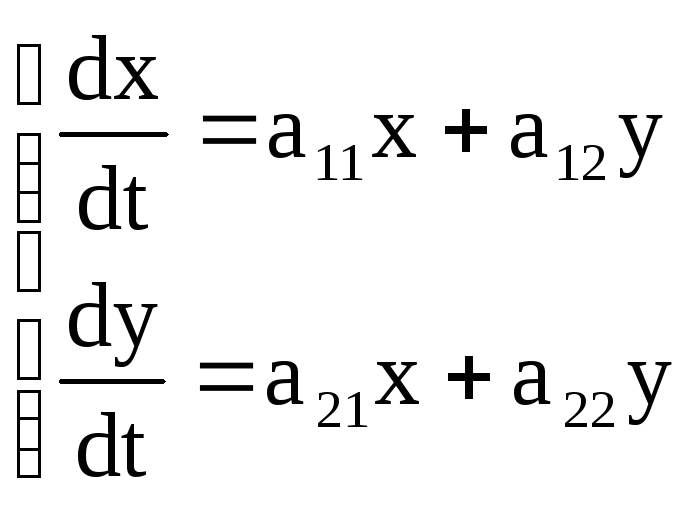. (1)

Исключим у из данных уравнений. Дифференцируем по t первое уравнение системы (1), при этом получим . Подставив в это равенство у^/ из второго уравнения системы, будем иметь

. (2)

Переписав первое уравнение системы в виде

(3)

и подставив это выражение в (2), получим уравнение

,

которое является ЛОДУ второго порядка с постоянными коэффициентами. Решая его, найдем функцию . Вторую функцию у системы (1) можно определить по формуле (3).

Схема решения:

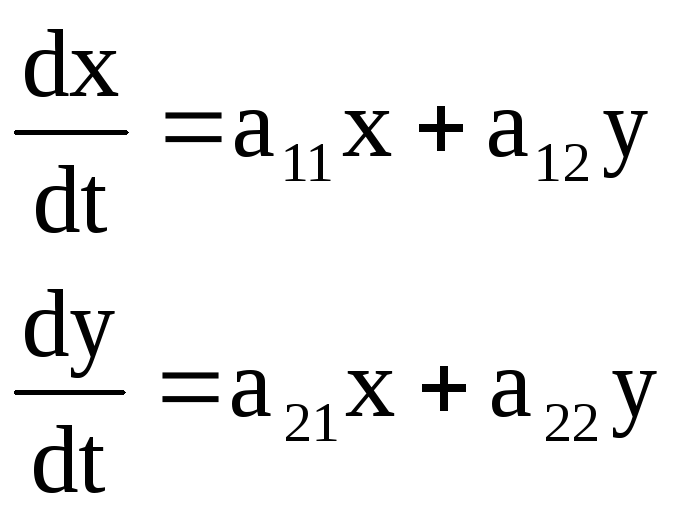
Пример 1. Найти общее решение системы (методом исключения)

.

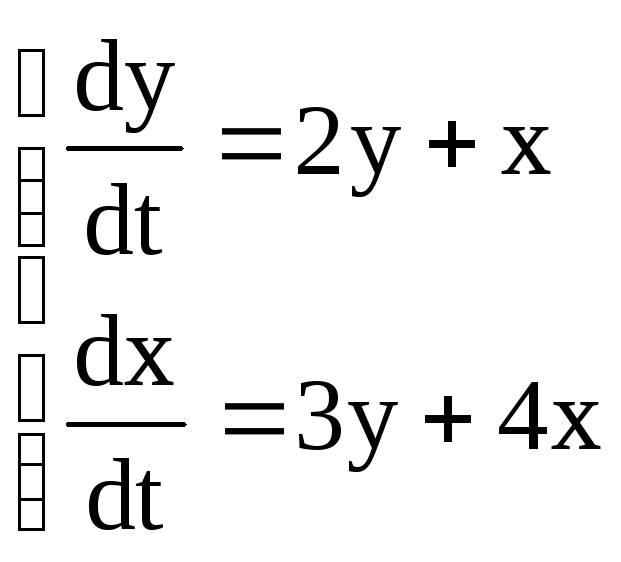Решение. Дифференцируя первое уравнение системы, будем иметь

Подставив сюда х^/ из второго уравнения системы, получим

.

Подставим х из первого уравнения, тогда

.

Приведем в последнем равенстве подобные члены:

.

Получим ЛОДУ второго порядка. Его характеристическое уравнение имеет два различных вещественных корня:. Следовательно, решением этого дифференциального уравнения будет:

, тогда.

Находим вторую функцию. Из первого уравнения имеем:

.

Ответ: .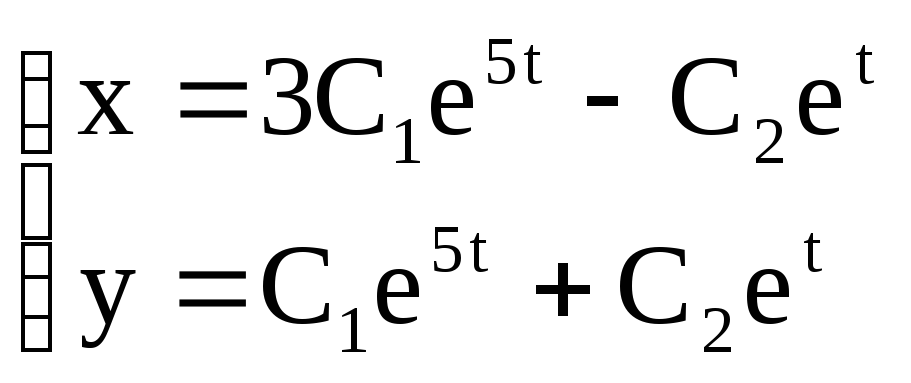

Пример. Решить систему

.

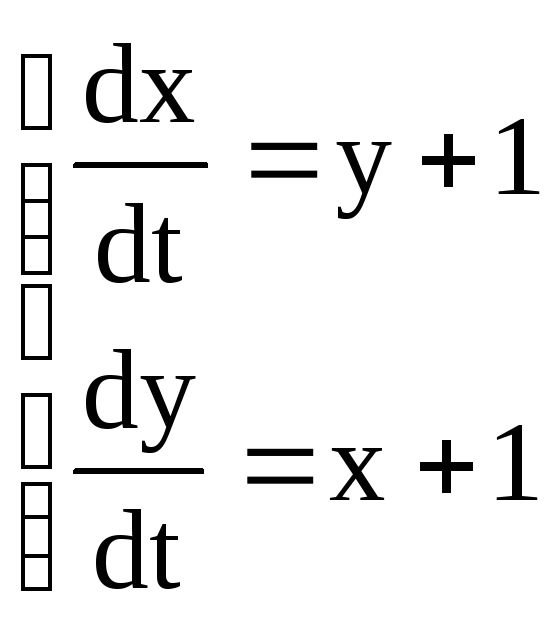Решение. Из первого уравнения системы находим

. Тогда. (_*)

Подставим это выражение во второе уравнение системы:

. (_**)

Получили линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его общее решение: , причем, что легко проверяется подстановкойв (_**). Найдем корни характеристического уравнения: . Следовательно,. Таким образом:

.

Дифференцируя это равенство и подставляя производную в (_**), получим

.

Общее решение системы:

.
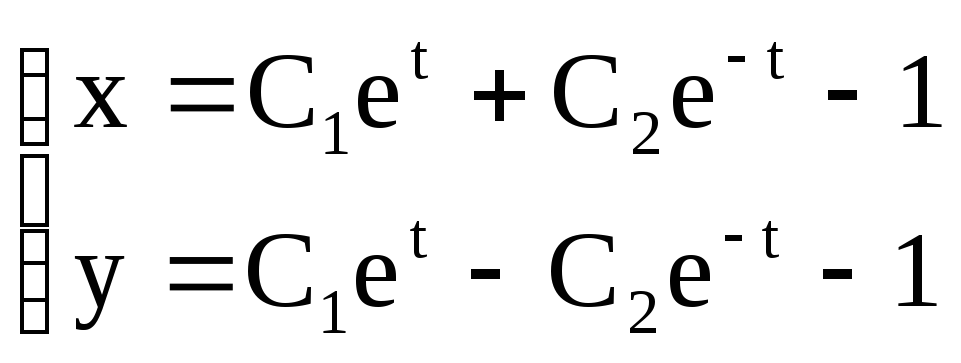