
- •Раздел 5
- •I. Обыкновенные дифференциальные уравнения (ду)
- •II. Дифференциальные уравнения высших порядков.
- •III. Системы обыкновенных дифференциальных уравнений.
- •Контрольная работа
- •I. Дифференциальные уравнения 1-го порядка.
- •Задание №1 для контрольной работы* . Найти общее решение дифференциального уравнения
- •II. Дифференциальные уравнения 2-го порядка, допускающие понижение порядка.
- •1) Дифференциальное уравнение вида (не содержащее искомой функции у).
- •Задание №2 для контрольной работы. Даны дифференциальные уравнения 2-го порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.
- •3) Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами со специальной правой частью:
- •Задание №3 для контрольной работы*.
- •III. Система линейных дифференциальных уравнений 1-го порядка с постоянными коэффициентами.
- •Задание №4 для контрольной работы .
- •IV. Составить дифференциальное уравнение и найти решение.
- •Задание №5 для контрольной работы.
- •Раздел 6 кратные интегралы
- •1. Двойной интеграл
- •2. Тройной интеграл
- •Задания для контрольной работы.
- •Раздел 7
- •Вопросы для самопроверки.
- •Вопросы для самопроверки
- •Вопросы для самопроверки.
- •Контрольная работа . Ряды. Уравнения математической физики.
- •4. Разложить в ряд Фурье функцию на указанном интервале.*
- •5. Методом Фурье решить уравнение колебаний конечной струны длины 1 с граничными условиямии начальными условиями
- •Раздел 8 криволинейные и поверхностные интегралы элементы теории поля
- •Задания для контрольной работы
- •Для заметок
II. Дифференциальные уравнения 2-го порядка, допускающие понижение порядка.
Рассмотрим два типа дифференциальных уравнений 2-го порядка, допускающие понижение порядка.
1) Дифференциальное уравнение вида (не содержащее искомой функции у).
Порядок такого
уравнения можно понизить, взяв за новую
неизвестную функцию
![]() ,
т.е. положить
,
т.е. положить![]() ,
следовательно
,
следовательно![]() .
Получим дифференциальное уравнениеI-го
порядка
.
Получим дифференциальное уравнениеI-го
порядка
![]()
Схема решений:
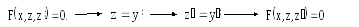
Получающееся при этом уравнение I-го порядка решаем одним из методов, рассмотренных ранее.
Пример 1. Найти
частное решение дифференциального
уравнения
![]() ,
,
удовлетворяющего
начальным условиям
![]() .
.
Решение.
Произведем понижение порядка
дифференциального уравнения. Положим
![]() ,
тогда
,
тогда![]() .
Подставив эти значения у/
и у//
в данное
уравнение, получим уравнение:
.
Подставив эти значения у/
и у//
в данное
уравнение, получим уравнение:
![]() ,
,
которое является уравнением с разделяющимися переменными. Разделим переменные:
![]() .
.
Производим
интегрирование
![]() .
Отсюда
.
Отсюда![]() .
Но
.
Но![]() ,
поэтому:
,
поэтому:
![]() .
(2)
.
(2)
Используем начальные
условия и найдем постоянную интегрирования
С1:
т.к.
![]() при
при![]() ,
то получаем
,
то получаем![]() ,
т.е. С1=3.
Тогда:
,
т.е. С1=3.
Тогда:
![]() .
(3)
.
(3)
Условие у=1 при х=0 подставим в (3): 1=С2. Таким образом, из начальных условий вытекает, что С1=3, С2=1 и искомое частное решение имеет вид:
![]() .
.
Замечание. Дифференциальное уравнение вида
![]()
приводится к
дифференциальному уравнению
![]() -го
порядка с помощью замены
-го
порядка с помощью замены![]() .
Например, пусть дано уравнение
.
Например, пусть дано уравнение![]() .
Положив
.
Положив![]() ,
понизим порядок на 2. Получим
,
понизим порядок на 2. Получим![]() - уравнение с разделяющимися переменными
(уравнениеI-го
порядка).
- уравнение с разделяющимися переменными
(уравнениеI-го
порядка).
2) Если в уравнение не входит независимое переменное х, т.е. уравнение имеет вид:
![]() ,
,
то порядок можно
понизить, взяв за новую независимую
переменную у, а за неизвестную функцию
![]() .
Тогда:
.
Тогда:
![]()
![]() .
.
Схема решения:
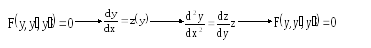
При этом получается
уравнение I-го
порядка относительно неизвестной
функции
![]() и независимой переменной у.
и независимой переменной у.
Пример 2. Найти
общее решение дифференциального
уравнения
![]() .
.
Решение. В
уравнение не входит х. Полагаем
![]() .
Тогда
.
Тогда
![]() .
.
После подстановки у/ и у// в исходное уравнение оно принимает вид
![]() или
или![]() .
.
Это уравнение с разделяющимися переменными. Решаем его:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
Следовательно,
![]() .
Тогда
.
Тогда
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
(При решении
уравнения делили на
![]() .
Если
.
Если![]() ,
т.е.
,
т.е.![]() ,
тогда
,
тогда![]() - это одно из решений данного уравнения,
не представляющее интереса).
- это одно из решений данного уравнения,
не представляющее интереса).
Задание №2 для контрольной работы. Даны дифференциальные уравнения 2-го порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.
|
2.1.
|
|
|
2.2.
|
|
|
2.3.
|
|
|
2.4.
|
|
|
2.5.
|
|
|
2.6.
|
|
|
2.7.
|
|
|
2.8.
|
|
|
2.9.
|
|
|
2.10.
|
|
|
2.11.
|
|
|
2.12.
|
|
|
2.13.
|
|
|
2.14.
|
|
|
2.15.
|
|
|
2.16.
|
|
|
2.17.
|
|
|
2.18.
|
|
|
2.19.
|
|
|
2.20.
|
|
|
2.21.
|
|
|
2.22.
|
|
|
2.23.
|
|
|
2.24.
|
|
3) Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами со специальной правой частью:
![]() , (p,
q
– const)
(1)
, (p,
q
– const)
(1)
Общее решение уравнения (1)
![]() ,
,
где
![]() - общее решение линейного однородного
дифференциального уравнения
- общее решение линейного однородного
дифференциального уравнения
![]() ,
,
![]() - некоторые частные
решения уравнения (1).
- некоторые частные
решения уравнения (1).
а) Рассмотрим решение ЛОДУ
![]() (2)
(2)
Схема решения (2):
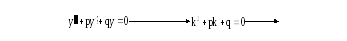

![]()
![]() (3)
(3)



![]()
![]() (4)
(4)

![]()
![]() (5)
(5)
Пример 1. Найти общее решение уравнений:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Решение.
а) составим характеристическое уравнение:
![]() .
.
его корни
![]() (1-ый случай). Общее решение исходного
дифференциального уравнения будет
согласно (3)
(1-ый случай). Общее решение исходного
дифференциального уравнения будет
согласно (3)
![]() .
.
б) Составим и решим характеристическое уравнение
![]() ,
,![]() (2-ой случай).
(2-ой случай).
Общее решение согласно (4) будет
![]() .
.
в) Составим и решим характеристическое уравнение
![]() ,
,![]() (3-ий случай).
(3-ий случай).
Общее решение согласно (5) будет
![]() .
.
б) Решение ЛНДУ. Рассмотрим метод подбора частного решения (метод неопределенных коэффициентов). Этот метод применим только к линейным уравнениям с постоянными коэффициентами и только в том случае, когда его правая часть имеет вид
![]() .
(6)
.
(6)
В этом случае частное решение ЛНДУ 2-го порядка
![]()
следует искать в виде
![]() .
(7)
.
(7)
Здесь r
равно числу совпадений контрольного
числа
![]() с корнями характеристического уравнения
(
с корнями характеристического уравнения
(![]() -
показатель экспоненты,
-
показатель экспоненты,![]() -
коэффициент при х в тригонометрических
функциях
-
коэффициент при х в тригонометрических
функциях![]() и
и![]() ).
).![]() и
и![]() - полные многочлены от х с неопределенными
коэффициентами, причемk
равно наибольшему из чисел m
и n
в (6), при этом если в
- полные многочлены от х с неопределенными
коэффициентами, причемk
равно наибольшему из чисел m
и n
в (6), при этом если в
![]() входит может быть одна из функций
входит может быть одна из функций![]() и
и![]() ,
то в (7) надо всегда вводить обе функции
,
то в (7) надо всегда вводить обе функции![]() и
и![]() .
.
Частными случаями
функции
![]() рассматриваемой структуры являются
следующие функции:
рассматриваемой структуры являются
следующие функции:
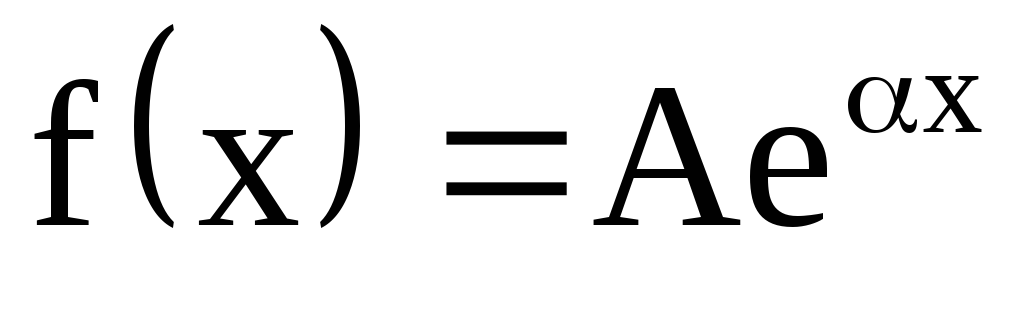 ,
А- постоянная,
,
А- постоянная,
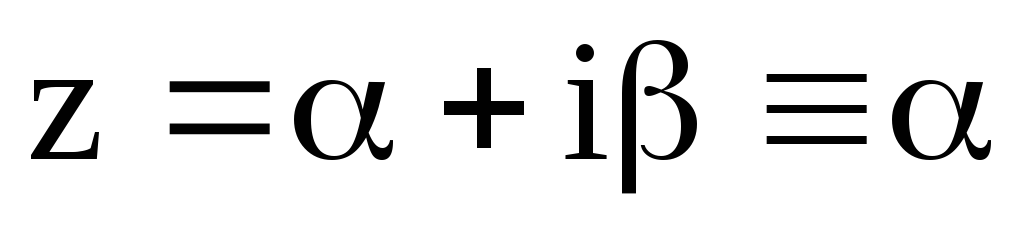 ;
;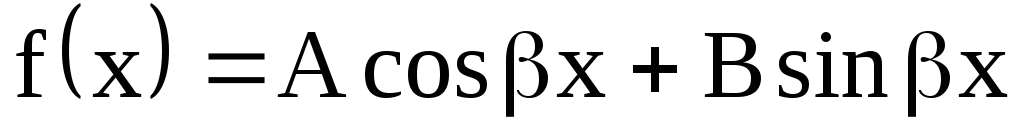 ,
А, В - постоянные,
,
А, В - постоянные,
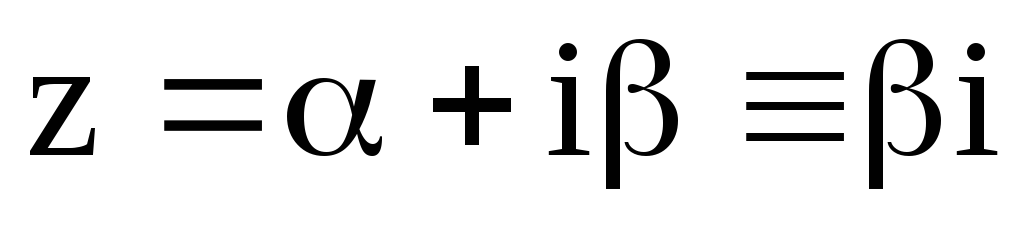 ;
;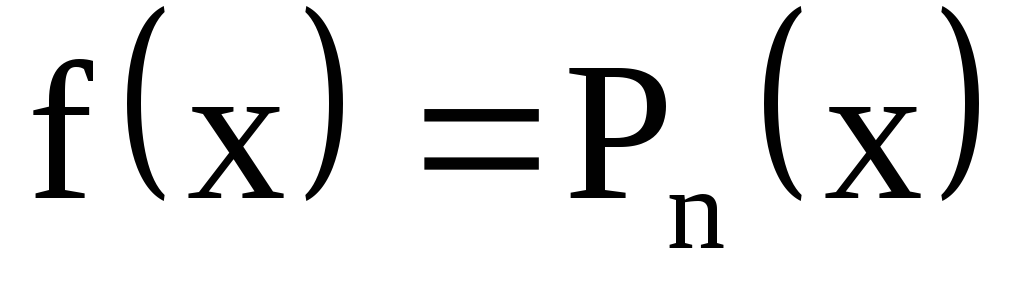 (многочлен степени
n),
(многочлен степени
n),
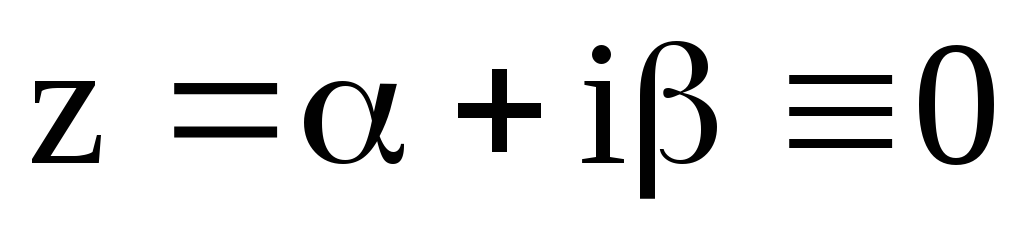 ;
;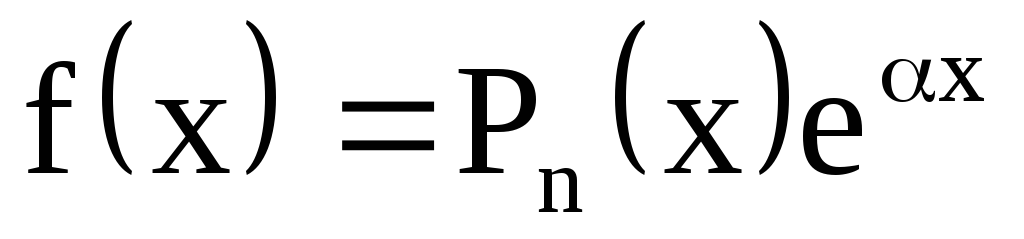 ,
,
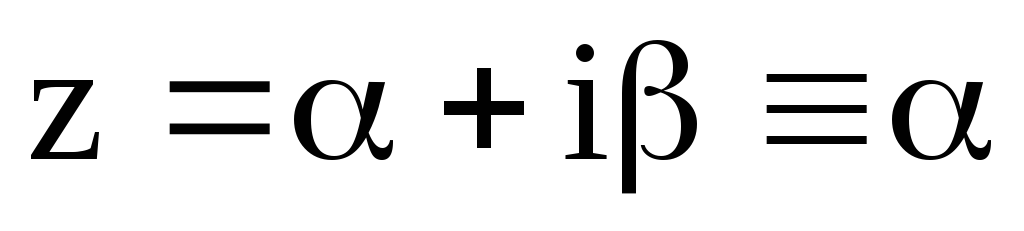 ;
; ,
,
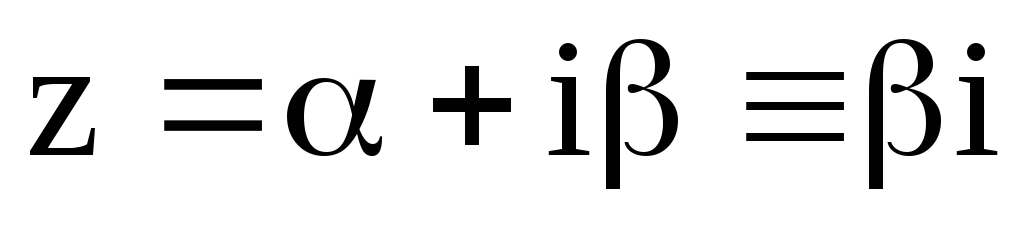 ;
;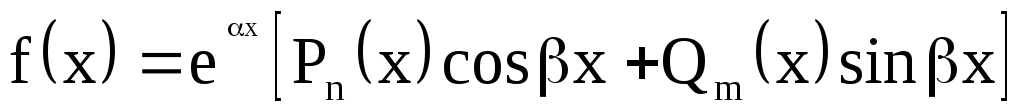 ,
,
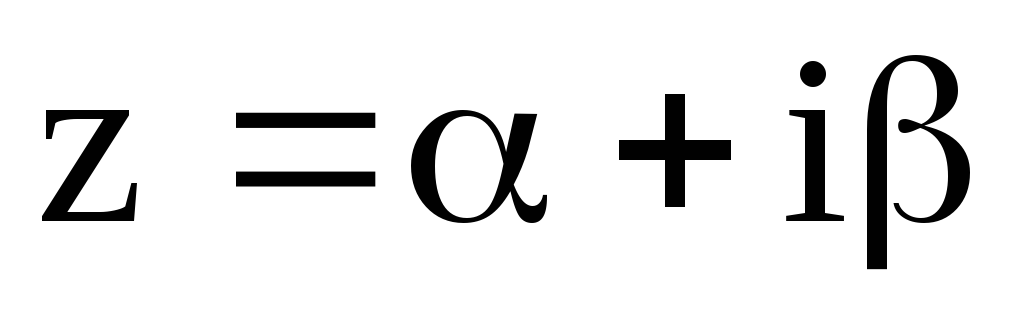 .
.
Если правая часть исходного уравнения равна сумме нескольких различных функций рассматриваемой структуры (6), то для отыскания частного решения надо найти частные решения, соответствующие отдельным слагаемым правой части, и взять их сумму, которая и является частным решением исходного уравнения. Например,
![]() ,
,
тогда
![]() ,
где
,
где![]() - частные решения уравнений
- частные решения уравнений
![]()
![]() .
.
Пример 2. Решить уравнение
![]() .
.
Решение.
а)
![]() - ЛОДУ. Составим характеристическое
уравнение
- ЛОДУ. Составим характеристическое
уравнение![]() .
Его корни
.
Его корни
![]() .
Тогда
.
Тогда
![]() .
.
б) Составим по
правой части
![]() контрольное число
контрольное число![]() .
Показатель экспоненты
.
Показатель экспоненты![]() равен 1. Функций
равен 1. Функций![]() и
и![]()
![]() не содержит. Итак, контрольное числоz
будет равно 1. Следовательно, число
совпадений
не содержит. Итак, контрольное числоz
будет равно 1. Следовательно, число
совпадений
![]() (т.к. совпадений
(т.к. совпадений![]() с корнями характеристического уравнения
нет). Тогда частное решение будем искать
в виде
с корнями характеристического уравнения
нет). Тогда частное решение будем искать
в виде
![]() .
.
Дифференцируем
![]() :
:
![]() .
.
Аналогично найдем
![]() .
.
Подставляя
![]() в исходное уравнение, получим
в исходное уравнение, получим
![]() .
.
Это равенство выполняется при всех значениях х, а значит, коэффициенты при одинаковых степенях х в левой и правой частях равенства совпадают. Приравнивая эти коэффициенты, получаем:
![]()
![]()
![]()
Таким образом,
![]() .
.
Пример 3. Составить вид частного решения следующих дифференциальных уравнений:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Решение.
а) Так как
![]() ,
,![]() ,
то
,
то
![]() .
.
Частное решение следует искать в виде
![]() ,
,
т.к. r=1
(есть одно совпадение контрольного
числа
![]() с корнем характеристического уравнения).
с корнем характеристического уравнения).
б) Так как
![]() ,
,![]() ,
то
,
то
![]() .
.
Контрольное число
![]() .
Частное решение следует искать в виде
.
Частное решение следует искать в виде![]()
(т.к. r=0, совпадений нет).
в)
![]()
![]()
![]()
![]()
![]() .
.
Так как
![]() ,
то
,
то![]() ,
,![]() .
Контрольное число
.
Контрольное число![]() равноz=i
; есть совпадение с корнем
равноz=i
; есть совпадение с корнем
![]() характеристического уравнения,
следовательно, частное решение следует
искать в виде
характеристического уравнения,
следовательно, частное решение следует
искать в виде
![]() .
.
