Министерство образования Российской Федерации

Нижегородский государственный университет им. Н.И.Лобачевского

Физический факультет

Отчет

по лабораторной работе

«Изучение упругих свойств

твёрдых тел»

Выполнил:

студент группы №511

Кучин Д.П.

Проверил:

Позднеев Д.Б.

г. Нижний Новгород

2003 г.

Цель работы: изучение деформации стальной проволоки в области линейной упругости.

Теоретическая часть.

Под действием силы или системы сил тело изменяет свою форму, или, как говорят, тело деформируется. В данной работе изучаются деформации растяжения.

Однородной деформацией называется такая деформация, при которой каждый элемент объема деформируется одинаково.

Рассмотрим простейший вид деформации  однородное растяжение. Величину деформации можно характеризовать относительным удлинением

(1)

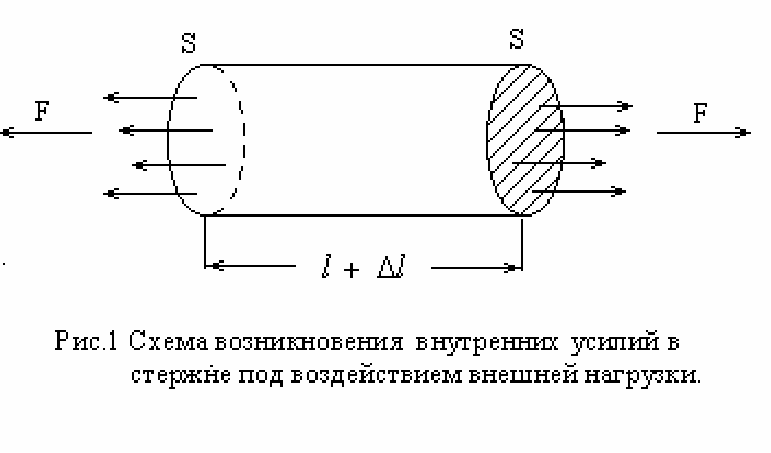г де  удлинение произвольного элемента стержня, имевшего первоначальную длину . Для всего стержня и любой его части величина одинакова и зависит от величины растягивающего усилия F, приложенного к концам стержня. Под действием силы F в стержне возникают внутренние силы (усилия), с которыми действуют друг на друга части стержня (рис.1).

Рис. 1. Схема возникновения внутренних усилий

в стержне под действием внешней нагрузки.

Из условия его равновесия следует, что силы, приложенные к концам этого кусочка со стороны соседних частей стержня, равны по величине и противоположны по направлению. Так как это справедливо для любого кусочка стержня, в любом поперечном сечении стержня возникают усилия, равные F.

Величину усилия, действующего на единицу площади поперечного сечения, называют напряжением в данном сечении и обозначают . В рассматриваемом примере направление внешней силы нормально к выбранной площадке и возникающее в этом случае внутреннее напряжение называется нормальным. Таким образом,

(2)

Опытным путем была установлена связь между относительным удлинением и нормальным напряжением . Например для стали, эта зависимость имеет вид (рис.2):

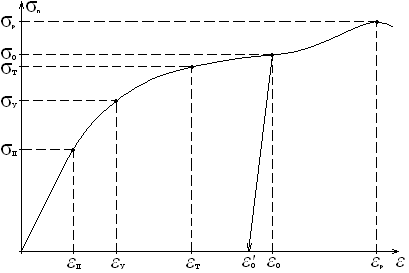
Рис. 2. Диаграмма растяжения стали.

Начальный участок кривой представляет собой прямую линию:

(3)

Соотношение (3) выражает так называемый закон Гука: относительное удлинение прямо пропорционально приложенному напряжению (т.е. растягивающему усилию на единицу площади F/S).

Коэффициент пропорциональности носит название модуля растяжения, или модуля Юнга. Для стали величина достигает н/м² (Па).

Закон Гука выполняется лишь при небольших деформациях. Максимальное напряжение ₁, при котором еще выполняется закон Гука, называется пределом пропорциональности (пределом линейной упругости), а эта область деформаций  областью пропорциональности.

При ε > ε_п линейная зависимость между ε и σ_n нарушается. Это область так называемой нелинейной упругости. Однако, и здесь при устранении внешних сил форма тела полностью восстанавливается.

Значение σ_у, после которого в теле появляются остаточные деформации, называется пределом нелинейной упругости. (Для стали предел линейной упругости лежит очень близко к пределу нелинейной упругости). Большинство металлов испытывает упругую деформацию до значений .

Участок кривой за пределом упругости называется областью пластических деформаций. Если довести величину деформации до значения ε_о, лежащего в области пластических деформаций, и полностью снять нагрузку, величина остаточной деформации будет почти такая же, как ε_о.

В этой области обычно отличают две характерные точки: предел текучести σ_т и предел прочности σ_р. При σ_n > σ_т материал «течет». Это означает, что нагрузка не возрастает, а деформации продолжают расти. Предел прочности σ_р  максимальное напряжение, при котором напряжение еще не разрушается; превышение этого предела ведет к разрушению испытуемого образца.

Методика эксперимента. Установка для изучения деформации растяжения.

Верхний конец проволоки укреплен на кронштейне А, нижний зажат винтом В (рис.3). При растяжении проволоки смещается оправа Д, соединенная с рычагом С, который может поворачиваться на шарнире ОО₁. Рычаг не позволяет проволоке раскачиваться. К оправе Д прикреплена миллиметровая шкала. Груз Р, растягивающий проволоку, помещается на платформу F (груз 1615г всегда лежит на платформе и служит для выпрямления проволоки).

Т.к. при изменении нагрузки изменяется прогиб кронштейна А, то смещение нижнего конца проволоки не равно ее удлинению. Чтобы избежать этого, к кронштейну прикреплены проволоки, на которых могут подвешиваться грузы Q. При измерении грузы Р и Q меняются так, чтобы их сумма оставалась постоянной. Тогда прогиб кронштейна будет постоянным, и смещение нижнего конца проволоки будет равно ее удлинению.

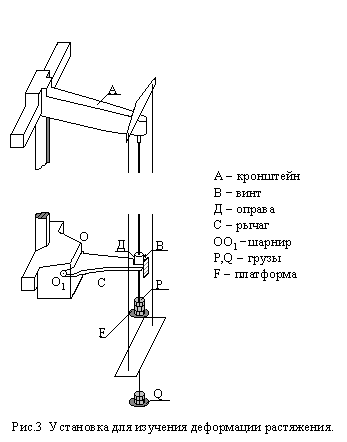
Рис. 3. Установка для изучения деформации растяжения.

Удлинение проволоки определяется по смещению одного из делений оправы Д. Измерение смещения производят измерительным микроскопом.

Измерительный микроскоп.

В фокальной плоскости окуляра измерительного микроскопа помещена нанесенная на стеклянной пластинке шкала. Чтобы можно было измерить предмет при помощи микроскопа, надо знать цену деления шкалы окуляра. Для этого микроскоп фокусируется на предмет, величина которого известна. В качестве такого предмета обычно берут несколько делений миллиметровой шкалы. Подсчитывают число делений m окулярной шкалы, укладывающихся в n делениях шкалы, видимой в микроскоп. Цена деления равна , где =1мм.

Практическая часть.

Приборы: линейка ( м), микрометр ( мм)

Во всех приведённых ниже расчётах погрешностей использовалась доверительная вероятность .

Измерение длины проволоки.

L₁ = 1.007 м, L₂ = 1.004 м, L₃ = 1.008 м, L₄ = 1.005 м, L₅ = 1.004 м.

По формуле (4) было рассчитано среднее значение длины проволоки численно равное L_ср = 1.0056 м.

(4)

По формулам (5) и (7) были рассчитаны абсолютная и относительная погрешности:

(5)

(6)

(7)

Они численно равны:

∆L = 0.0024 м; ε = 0.0024.

Измерение диаметра проволоки.

d₁ = 1.21 мм, d₂ = 1.19 мм, d₃ = 1.20 мм, d₄ = 1.19 мм, d₅ = 1.20 мм.

По формуле (4) было рассчитано среднее значение диаметра проволоки численно равное d_ср = 1.198 мм.

По формулам (5) и (7) были рассчитаны абсолютная и относительная погрешности численно равные:

∆d = 0.013 мм; ε = 0.0103.

Расчет модуля Юнга для стали.

Цена деления окулярной шкалы микроскопа () равна 1/17 мм.

Сняв зависимость удлинения проволоки ∆L от нагрузки F по методике, указанной выше, были получили получены следующие результаты:

№	М, гр.	∆L, мм.
1	0	0
2	677	0.059
3	1232	0.118
4	2384	0.235
5	3337	0.294
6	4263	0.353
7	5416	0.471
8	6341	0.529

Качественно экспериментально полученные данные отображены на рис. 4:

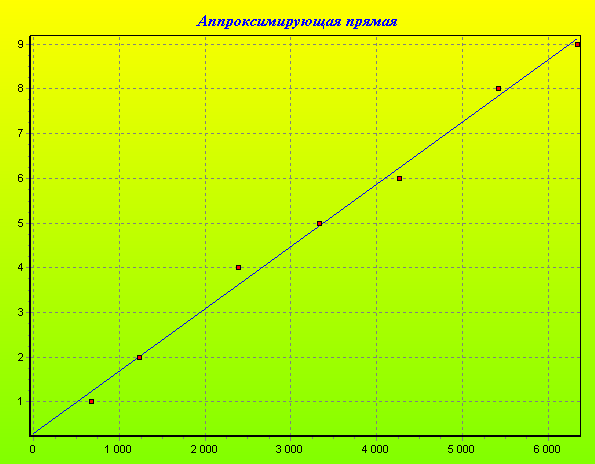
Рис. 4.

Теория указывает на наличие зависимости между величинами mg и ∆L. Из формул (2) и (3) получаем следующий вид этой зависимости:

(8)

То есть, согласно теории, между величинами mg и ∆L должна существовать линейная зависимость. Проверим это утверждение, используя результаты эксперимента.

Рассчитаем коэффициент корреляции (R) для полученной зависимости по формуле:

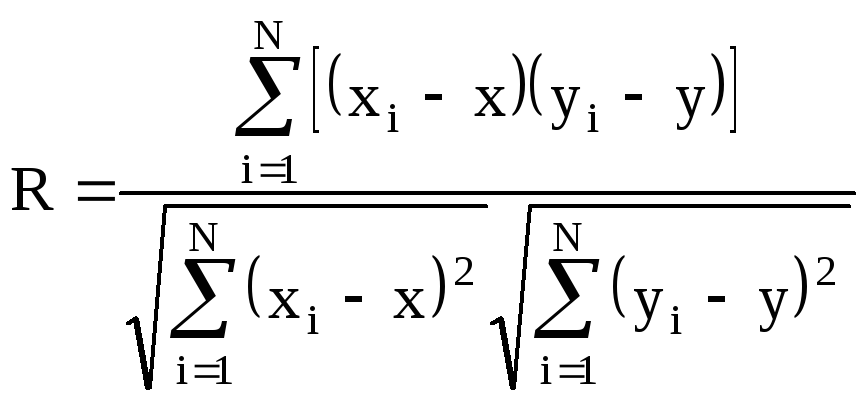(9)

где пар числовых значений, полученных экспериментально (i=1,…); и средние статистические результаты измерений.

Подставив, экспериментально полученные, численные значения в выражение (9) получим численное значение приближенного значения коэффициента корреляции:

R=0.9999

Оценка коэффициента корреляции, столь близкая к единице, является убедительным доказательством наличия линейной зависимости между величинами и экспериментальным подтверждением теоретической формулы (8).

Теперь, используя результаты эксперимента, методом наименьших квадратов для прямопропорциональной зависимости подсчитаем угловой коэффициент функции (8). Неизвестная постоянная β в функции ∆L = βmg заменяется переменной b₀.

Из уравнения (10), подставив численные значения полученные экспериментально, было вычислено численное значение b₀:

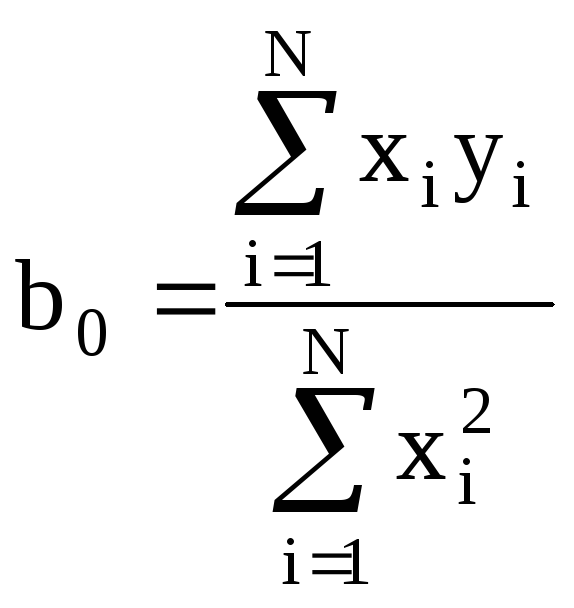(10)

b₀ = 8.745·10^-6 с²/ м·кг

Формула (11) дает нам значение наилучшего приближения углового коэффициента β прямопропорциональной зависимости (8) (β ≈ b₀).

Рассчитаем границы доверительного интервала для β. Опираясь на выводы математической статистки, выражаем среднеквадратичное отклонение случайной величины b₀, вычисляемой по формуле (11), от истинного углового коэффициента β:

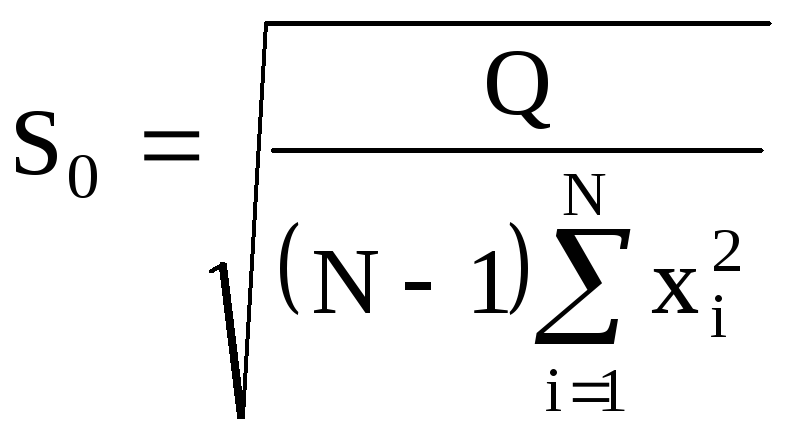(11)

Доверительный интервал для углового коэффициента β прямо пропорциональной зависимости (8) запишется в виде:

(12)

Абсолютная погрешность углового коэффициента β равна полуширине доверительного интервала:

(13)

где  коэффициент Стьюдента для установленной доверительной вероятности  и числа степеней свободы, равной (N-1).

Найдем Q, подставив вычисленное b₀ в уравнение (14):

(14)

Q = 0.515

Отсюда

S₀ = 1.476·10^-7

∆β = 0.349·10^-6 c²/м·кг,  = 0.95

Выразим относительную погрешность модуля Юнга:

(15)

где среднее значение модуля Юнга E = 4L / π₀·d²·b₀ (символом ₀ обозначено округленное значение числа ). при ₀ = 3.142.

ε_E = 0.0449264

E_ср = 10.20·10¹⁰ Па

∆E = ε_E · E_ср = 0.46·10¹⁰ Па

E = (10.20 ± 0.46) · 10¹⁰ Па

Вывод: в процессе работы было произведено ряд экспериментов, после чего на основании теоретических расчётов было получено численное значение модуля Юнга. Нетрудно заметить, что полученный результат лежит ближе всего к табличному значению модуля Юнга для стали Е = 2021·10¹⁰ Па. Из чего можно сделать вывод, что исследуемый нами материал действительно сталь.