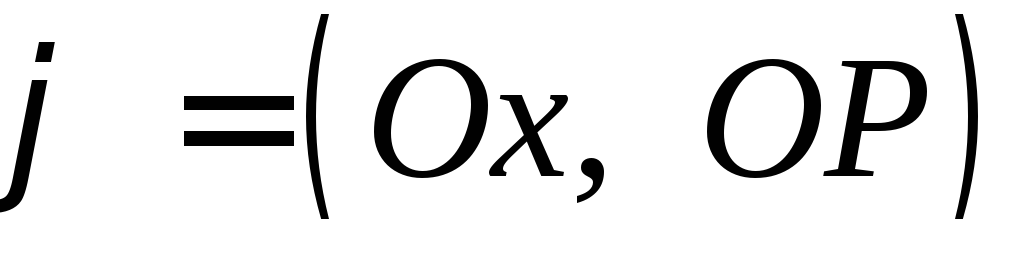§ 104. Директрисы эллипса

Две прямые, перпендикулярные оси эллипса, на которой расположены его фокусы, и отстоящие от центра эллипса на расстоянии , где а - большая полуось эллипса, а е - его эксцентриситет, называются директрисами эллипса.

Окружность, для которой е = 0 не имеет директрис т.е. понятие директрис дается только для эллипса.

Если эллипс задан каноническим уравнением, причем (т.е. фокусы расположены на оси Ох) то уравнения директрис имеют вид:

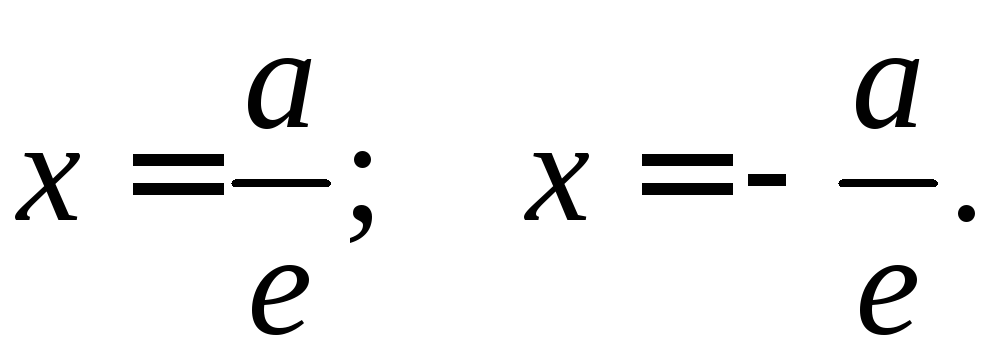
Так как ; то 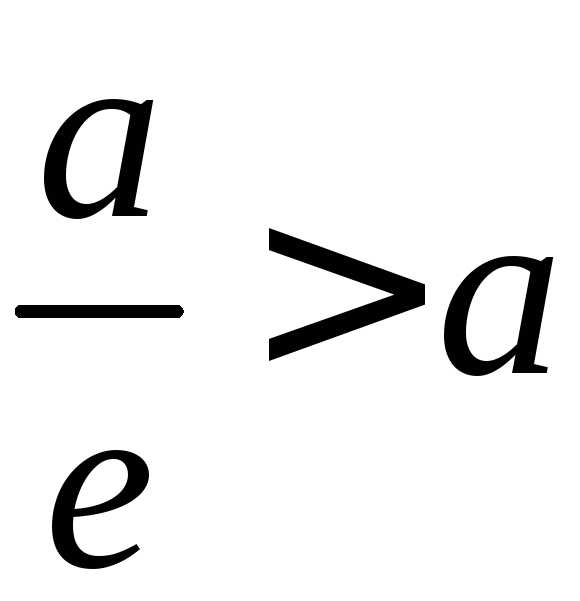, и, значит, директрисы эллипса отстоят от его центра дальше, чем вершины (см. рис.). Фокус и директриса эллипса, расположенные по одну сторону от меньшей оси эллипса, называются соответствующими друг другу.

Таким образом, фокусы соответствует директриса 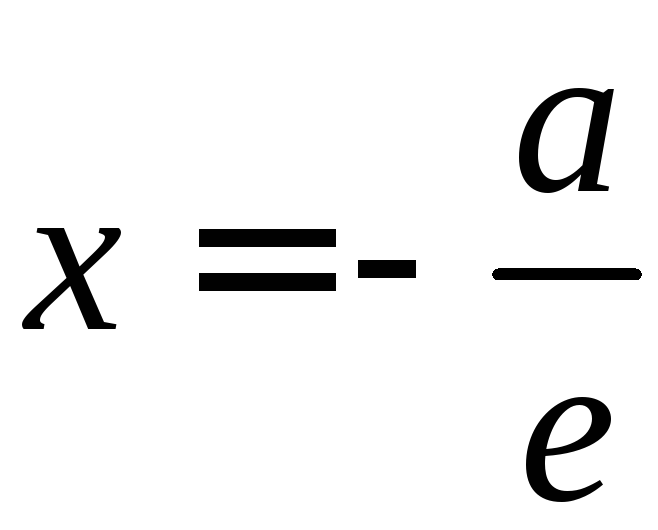, а фокусу - директриса.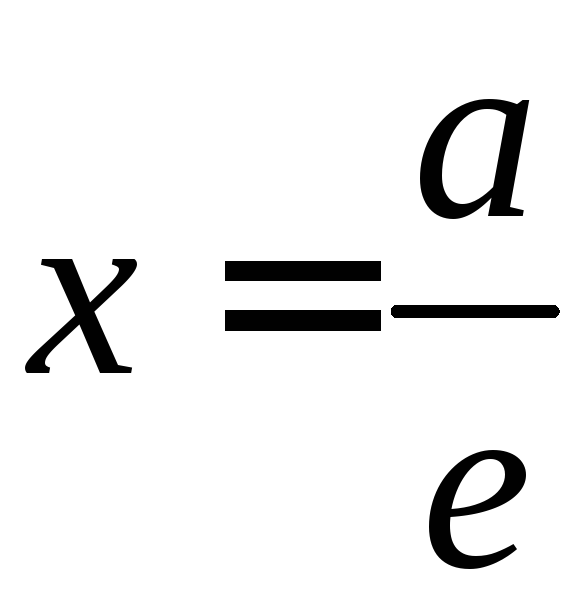

Теорема. Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния от этой точки до фокуса эллипса к расстоянию от той же точки до директрисы, соответствующей рассматриваемому фокусу, было равно эксцентриситету эллипса.

Доказательство: Необходимость. Рассмотрим, например, фокус и соответствующую ему директрису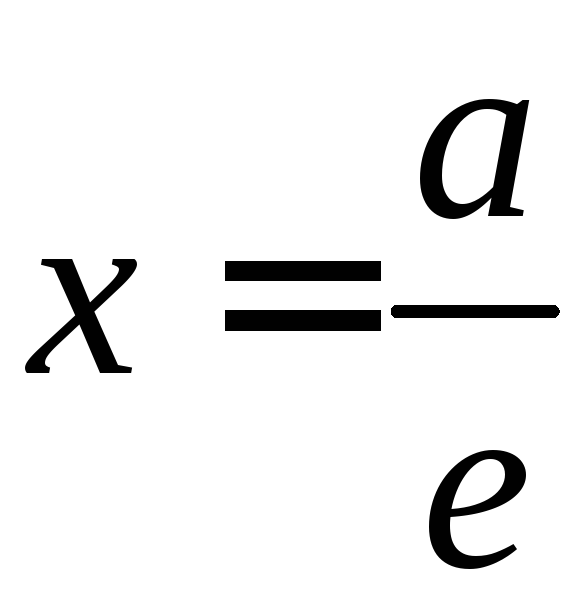. Расстояниеот точкиМ(х, у) до

ф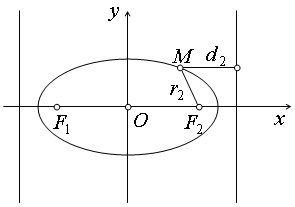окусавычисляется по формуле.

Расстояние от той же точкиМ(х, у) эллипса до прямой 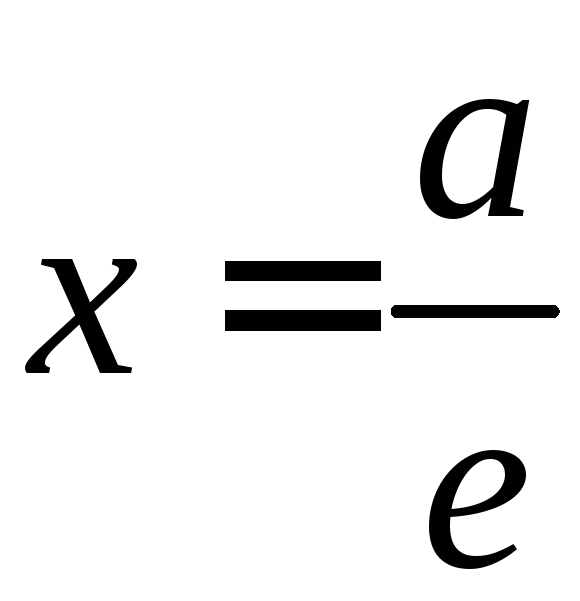вычисляется по формуле.

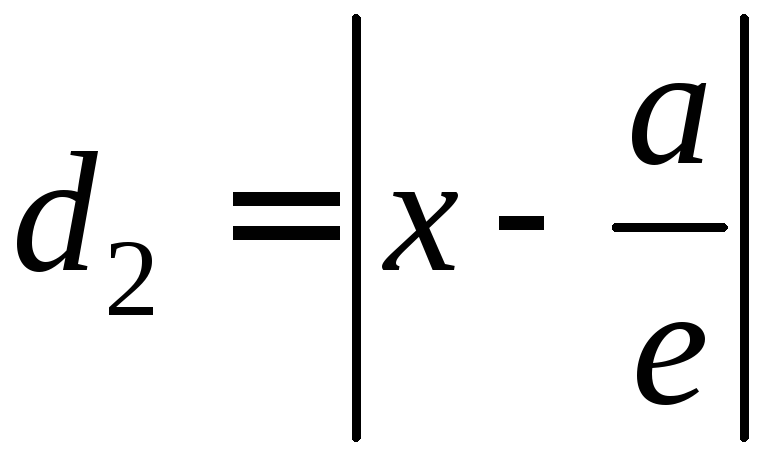Итак: .

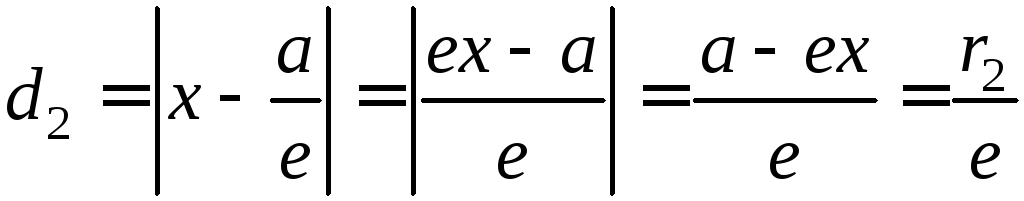Отсюда 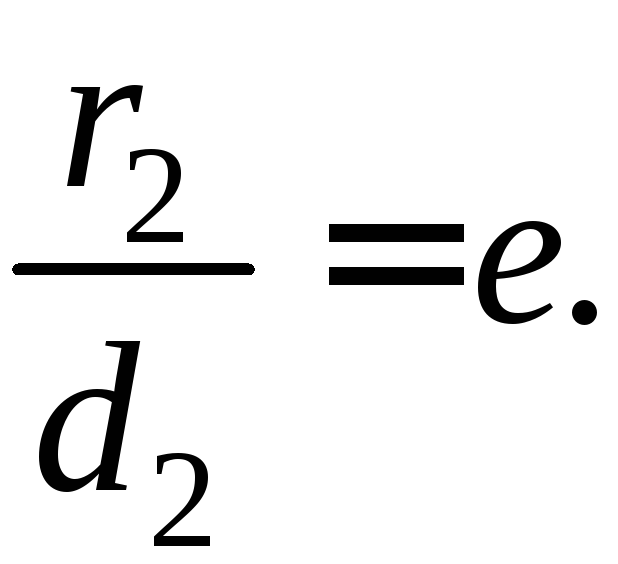Теорема доказана.

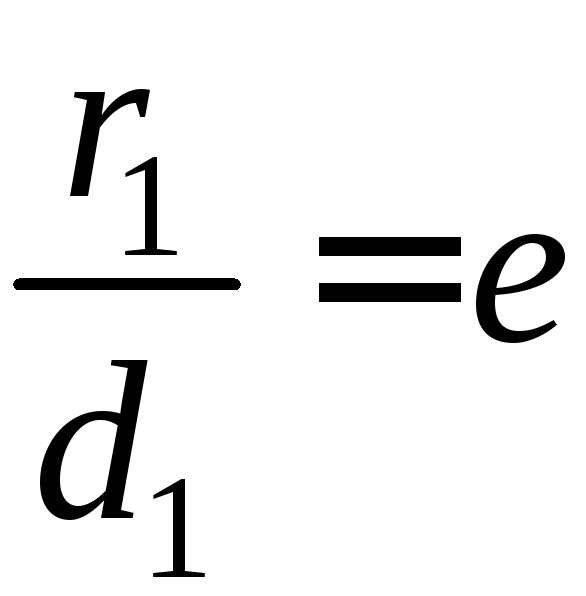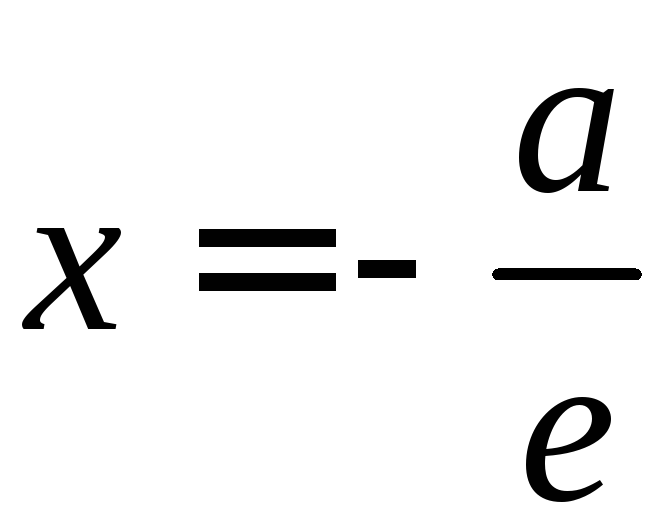Аналогично доказывается, что , где, есть расстояние от точкиМ до фокуса , а- расстояние от той же точки до директрисы, соответствующей фокусу.

Доказательство достаточности.

Возьмем каноническое уравнение эллипса, где a > b. Рассмотрим, например, фокус этого эллипса и соответствующую ему директрису.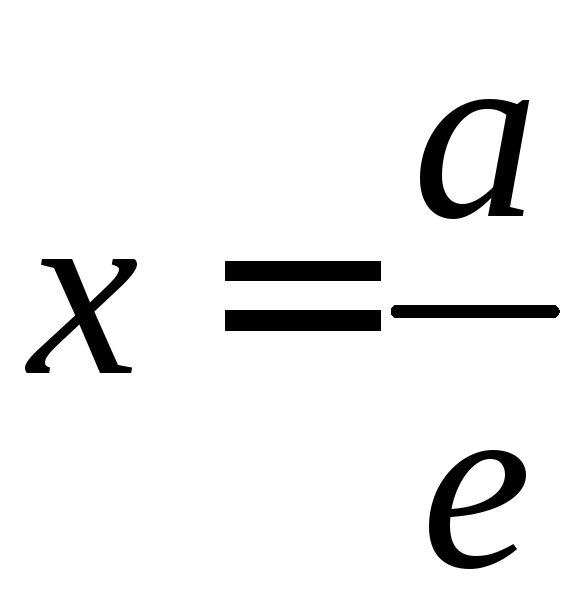

Пусть М(х, у) такая точка, что

,

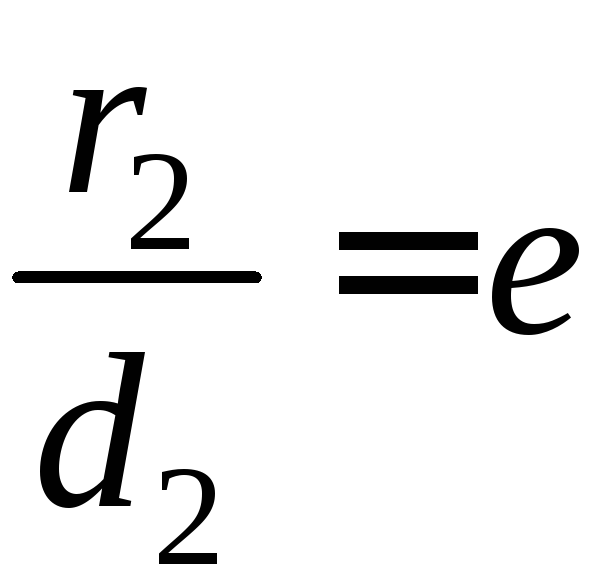где - расстояние от точкиМ до фокуса , а- расстояние от точкиМ до директрисы .

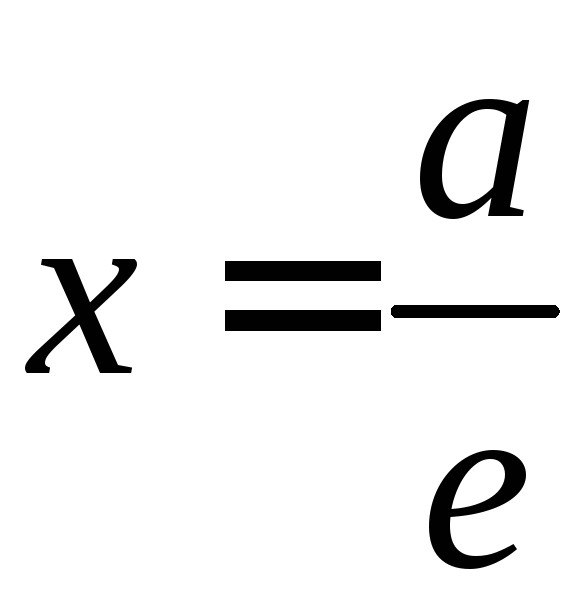Докажем, что точка М(х,у) лежит на эллипсе.

В самом деле, т.к.

; ,

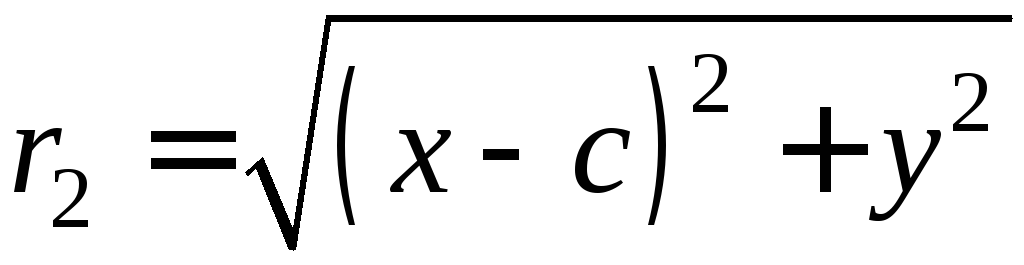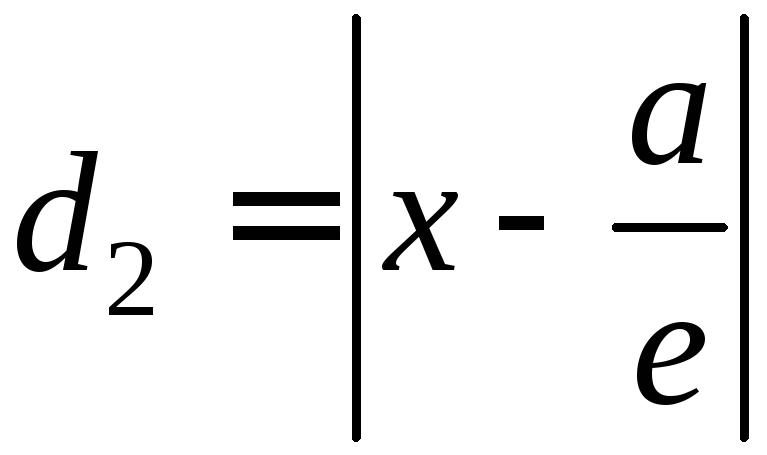то из соотношения

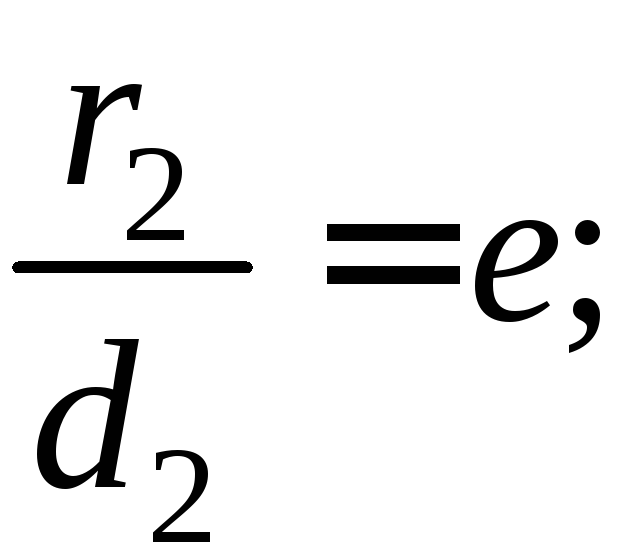или ,

находим:

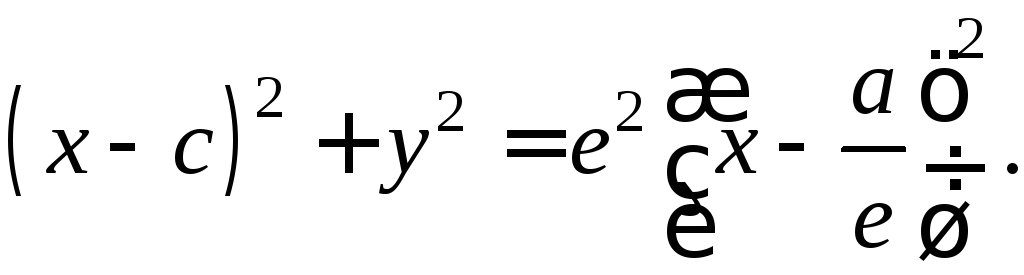
Упрощая это уравнение, получим 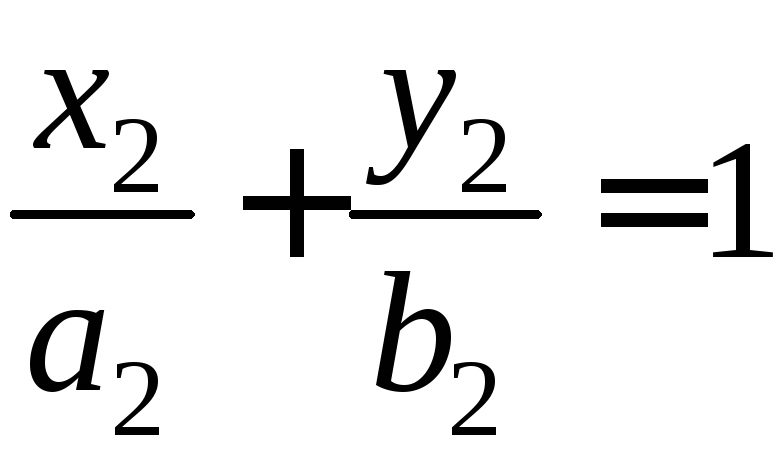. А это означает, что точкаМ(х, у) ежит на эллипсе.

Расстояние m от фокуса эллипса до его директрисы равно

,

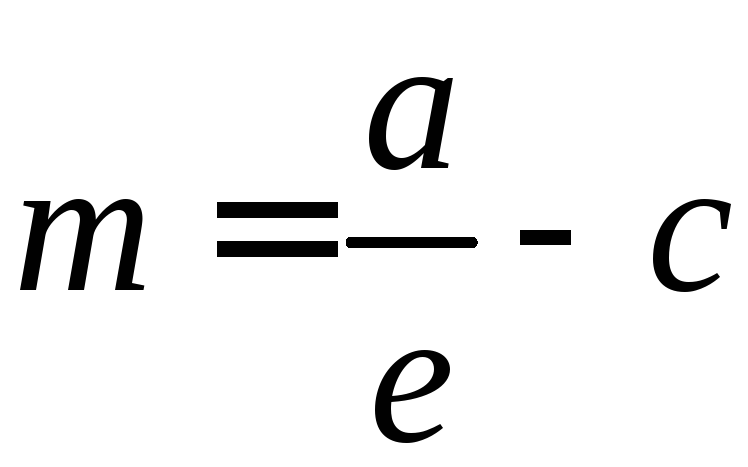а эксцентриситет определяется формулой:

.

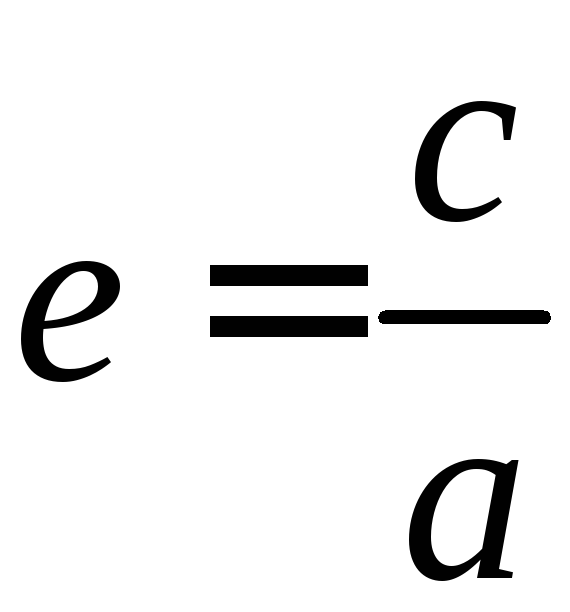Из этих соотношений находим

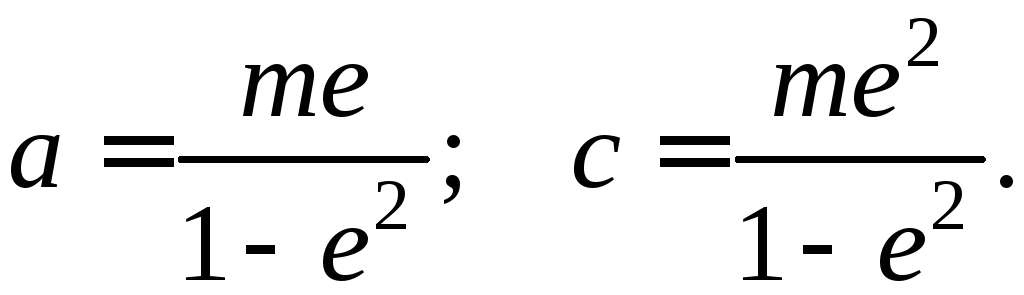
Отсюда следует, что если на плоскости задана произвольно точка , прямая, не проходящая через эту точку(отстоящая от точкина расстоянии ) и задано произвольное положительное число е, меньшее 1, то существует эллипс, для которого точка - фокус, заданная прямая – директриса, ае - эксцентриситет. Центр этого эллипса находится на расстоянии

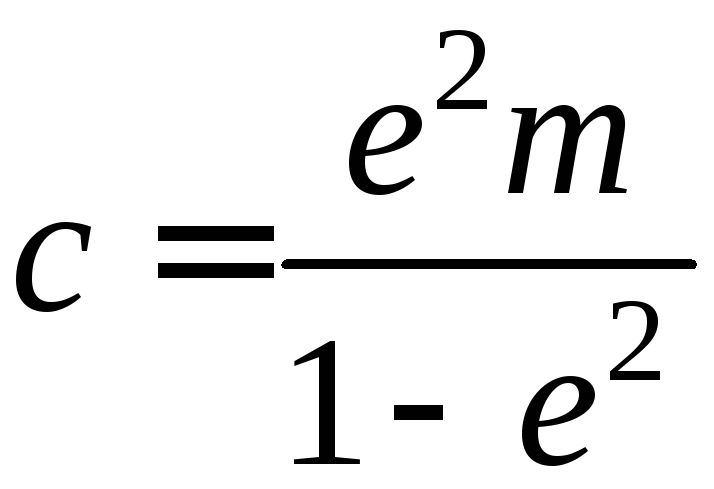
от точки (по одну сторону с точкойот данной прямой), а большая полуось

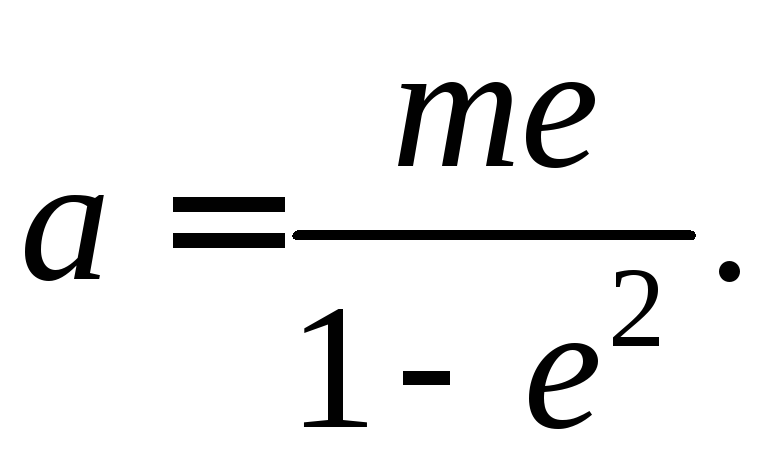
Отсюда и из только что доказанной теоремы следует, что эллипс можно определить как геометрическое место точек, для каждой из которых отношение расстояния от данной точки к расстоянию до данной прямой, не проходящей через точку, равно данному положительному числу, меньшему 1.

Исключением является окружность, которая данным свойством не обладает.

§ 106. Параметрические уравнения эллипса

Пусть дан эллипс каноническим уравнением 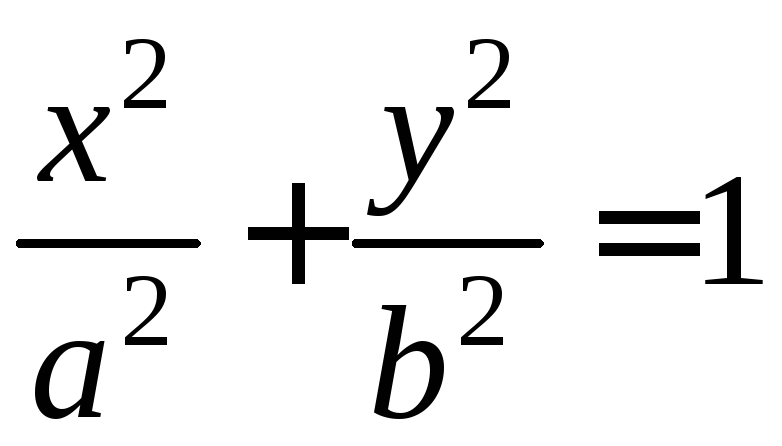. (1)

Рассмотрим окружность

, (2)

которая переходит в данный эллипс в результате сжатия

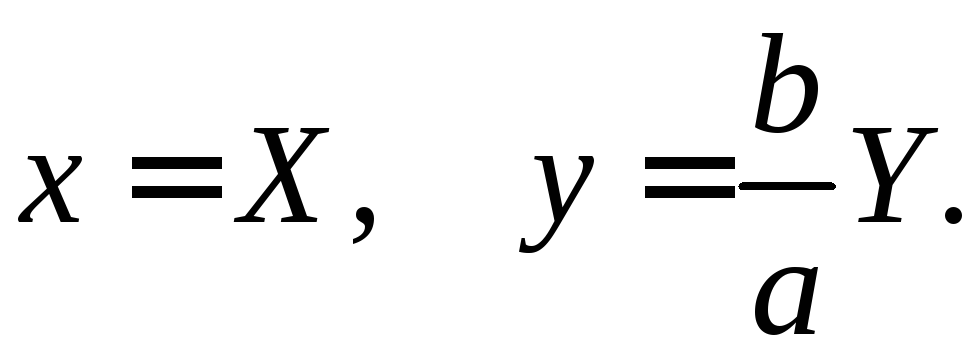(3)

Пусть М(х, у) – произвольная точка данного эллипса, - ее образ на окружности. Обозначим черезугол от положительного направления осиОх до луча ОР.

Тогда

и, следовательно,

.

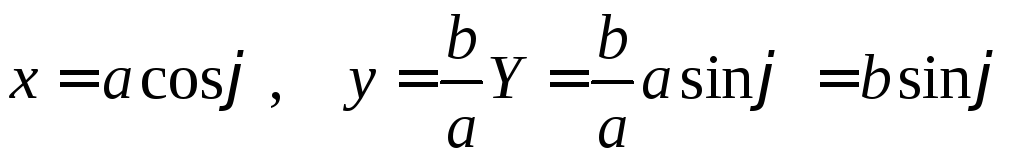У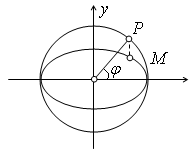равнения

И являются параметрическими уравнениями эллипса.

Параметр называется эксцентрическим углом точки эллипса. Если задана точкаэллипса, то для нахождениянадо построить окружность на большей оси эллипса как на диаметре и через точку М провести прямую, параллельную малой оси эллипса.

Точка пересечения этой прямой с окружностью, лежащая по ту же сторону от большей оси эллипса, что и точкаМ, является прообразом точки М(х,у) при равномерном сжатии 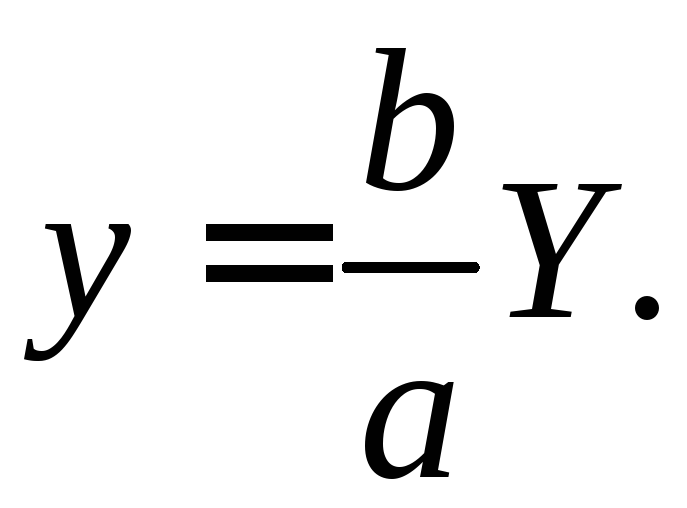Угол от осиОх до луча ОР и являются эксцентрическим углом , соответствующим взятой точкиМ на эллипсе (см. рис.).