Задача 8. Построение эллипсоида напряжений Построить эллипсоид напряжений.

Геометрические образы напряженного состояния в точке: куб, эллипсоид, шар (если сопряженные диаметры эллипсоида равны друг другу), треугольник напряжений, звезда напряжений, диаграмма Мора.

Эллипсоид напряжений - это объемный геометрический образ напряженного состояния (см. рисунок 4). Если провести через рассматриваемую точку М деформируемого тела площадку с нормалью h, то конец вектора полного напряжения S_n на этой площадке лежит на поверхности эллипсоида. Уравнение эллипсоида напряжений:

.

Его полуоси равны , , , а поверхность является поверхностью напряжений, т. е. любая ее точка N является концом вектора напряжений S_n действующего на одной из площадок , проходящей через рассматриваемую точку.

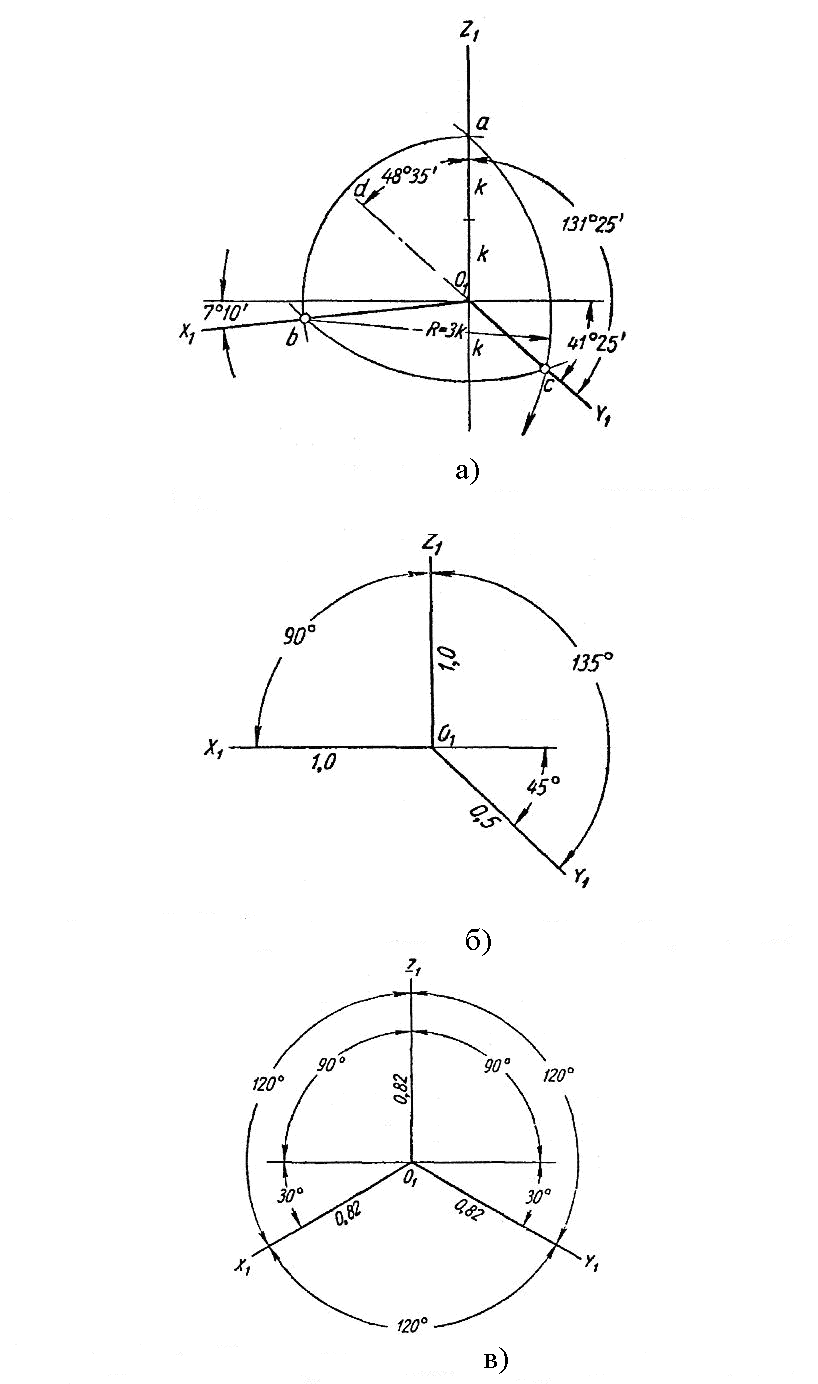
Выбираем одну из пяти аксонометрических проекций в соответствии с ГОСТ 2.317-69 «Аксонометрические проекции» с измерением №1, утвержденным в августе 1980 года:

1) прямоугольную изометрическую проекцию;

2) прямоугольную диметрическую проекцию;

3) косоугольную фронтальную изометрическую проекцию;

4) косоугольную горизонтальную изометрическую проекцию;

5) косоугольную фронтальную диметрическую проекцию.

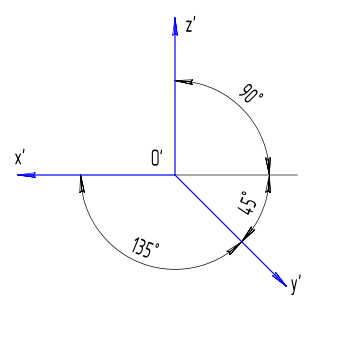
г)

д)

Рисунок 15 - прямоугольная диметрическая проекция(а), косоугольная фронтальная диметрическая проекция (б), прямоугольная изометрическая проекция(в), косоугольная фронтальная изометрическая проекция(г), косоугольная горизонтальная изометрическая проекция(д)

Аксонометрическая проекция — наглядное изображение, полученное методом параллельного проецирования на одну плоскость, называемую аксонометрической.

х, у, z - система пространственных осей.

х', у', z' - аксонометрические оси.

Коэффициент искажения (к) — называется величина отношения единичного отрезка, взятого на аксонометрической оси к его натуральной величине.

Виды аксонометрических проекций.

Классификация аксонометрических проекций ведётся по двум признакам:

1)по направлению аксонометрических лучей:

а) прямоугольные,

б) косоугольные.

2) В зависимости от соотношения коэффициентов искажения по аксонометрическим осям:

а) если - изометрия;

б) если - диметрия;

в) если - триметрия.

Выбираем такую проекцию, чтобы плоское изображение эллипсоида на рисунке было наиболее наглядным.

Рассмотрим последовательность построения эллипсоида. Через точку М проводим три главные оси тензора напряжений , , . Они взаимно перпендикулярны, но углы между ними на рисунке зависят от выбора аксонометрической проекции.

На осях , , по обе стороны от начала координат (точки М) в выбранном масштабе и с учетом коэффициентов искажения откладываем отрезки, соответственно равные , , . Получаем три сопряженных диаметра эллипсоида АВ, CD, EF.

Строим три эллипса, которые являются линиями пересечения поверхности эллипсоида с координатными плоскостями. В координатной плоскости эллипс строим по двум сопряженным диаметрам АВ и CD. В координатной плоскости эллипс строим по сопряженным диаметрам CD и EF. В координатной плоскости эллипс строим по двум сопряженным диаметрам EF и АВ.

На рисунке 5 показано, как строить эллипс по двум сопряженным диаметрам KL и RS. Вначале строим параллелограмм, стороны которого проходят через точки К, L, R, S и параллельны диаметрам KL и RS. Диаметр RS делим на несколько равных частей. На столько же равных частей делим стороны, параллельные диаметру KL. Точки деления обозначаем, как показано на рисунке. Из точек К и L проводим через точки деления лучи. Поводим эллипс через точки К, L, R, S, а также через точки пересечения одноименных лучей.

Проводим четвертый эллипс, огибающий три уже построенные в координатных плоскостях. Он и является аксонометрической проекцией эллипсоида. В заключение выделяем видимые и невидимые линии эллипсов, расположенных в координатных плоскостях.

Задача 9. Вычисление интенсивности напряжений и угла вида напряженного состояния

Вычислить интенсивность напряжений, интенсивность касательных напряжений и угол вида напряженного состояния.

Девиатором называется симметричный тензор 2-го ранга, первый инвариант которого равен нулю:

.

Второй и третий инварианты девиатора в прямоугольной и декартовой системах координат равны:

Интенсивность напряжения равна:

⁽²⁴⁾

где индекс «и» означает «интенсивность».

Для контроля вычисляем аи также через главные нормальные напряжения:

(25)

При одноосном растяжении (сжатии) интенсивность напряжений равна единственному нормальному напряжению:

Интенсивность касательных напряжений Т равна:

(26)

При сдвиге интенсивность касательных напряжений равна: Т = . Это скалярная величина, характеризующая напряженное состояние. Угол вида напряженного состояния равен:

(27)

где третий инвариант девиатора напряжений находим по формуле:

. (28)

По формуле (28) среднее напряжение, или гидростатическое давление, равно:

(29)

Определитель (28) можно вычислить по формуле Саррюса.

Для контроля вычисляем также через главные нормальные напряжения:

(30)

Задача 10. Построение треугольника напряжений

Построить треугольник напряжения. Графически найти интенсивность напряжений и угол вида напряженного состояния, сравнить с результатами расчетов и в задаче 9.

Угол = BCD называется углом вида напряженного состояния. Угол вида напряженного состояния характеризует напряженное состояние, но лишь с точностью до среднего напряжения, поскольку величина а не влияет на геометрическое построение треугольника напряжений. При линейном растяжении = 0, при линейном сжатии , при простом сдвиге .

Выбрав масштаб, строим равносторонний треугольник ABC, стороны которого равны ( - ) (см. рисунок 6). Одну из его сторон, например АВ, точкой D делим на две части: AD = ( - ) и DB = ( - ). Точку D соединяем прямой линией с противоположной вершиной треугольника С. Тогда длина отрезка прямой CD в выбранном масштабе равна интенсивности напряжений .

Угол BCD равен углу вида напряженного состояния . =22,5; = 22,8. Полученные значения хорошо согласуются с результатами расчетов в п.9. Применяя теорему синусов к треугольнику BCD:

.

получим формулу (30):

Рассмотрим треугольник BCD. Согласно теореме косинусов, получим, что . После преобразования (раскрытия скобок, приведения подобных), получим: .

Задача 11. Построение звезды напряжений

Построить звезду напряжений. Графически найти главные нормальные и главные касательные напряжения, сравнить с результатами расчета главных напряжений в задаче 6.

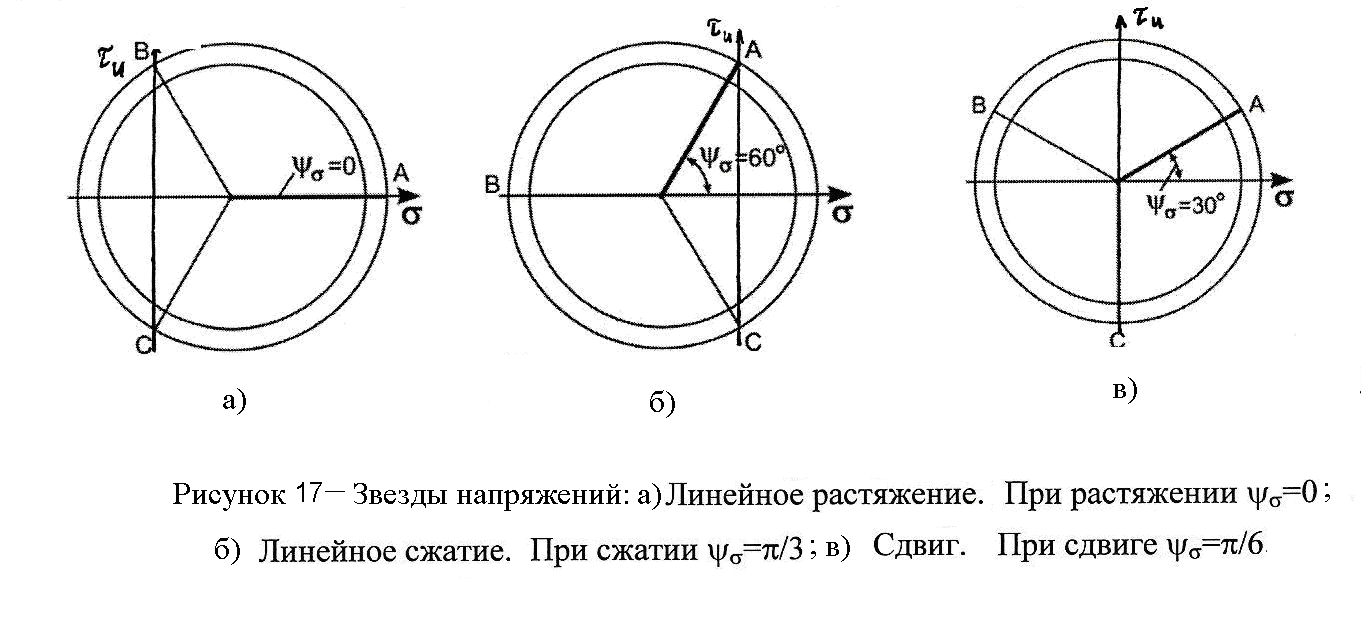
Звезду напряжений строим в координатах (нормальное напряжение), (касательное напряжение) (рисунок 17). Центр звезды - точка М находится на оси . Координата центра звезды равна среднему напряжению (формула 29).Проводим две окружности, с центром в точке М. Радиус большей окружности равен . Радиус меньшей окружности равен интенсивности касательных напряжений . Из точки М проводим три луча, образующие собственно звезду, углы между которыми равны 120°. Угол между первым лучом МА и осью равен углу вид напряженного состояния .

Луч ОА составляет с осью угол , тогда абсциссы точек А, В, С равны главным нормальным напряжениям. Т. е. длина проекции отрезка ОА' на ось будет равна:

С учетом выбранного масштаба, абсциссы точек пересечения лучей с большой окружностью равны главным нормальным напряжениям , , . Ординаты точек пересечения лучей с малой окружностью равны главным касательным напряжениям , , :

=14,514; =-1,206; =-11,308;

=7,86; =5,051; =-12,911.

Полученные данные согласуются с результатами расчетов в задаче 6.