Устойчивость периодических движений
Рассмотрим устойчивость периодического решения
(1)
системы дифференциальных уравнений
,
(2)
подробно записанной в виде
.
(3)
Возмущение решения
,
.
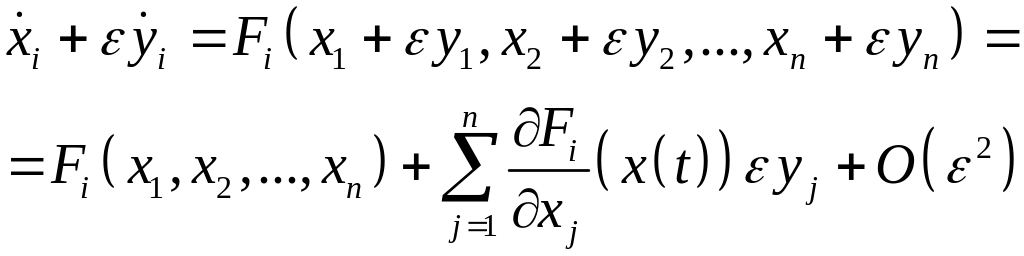(4)
Отсюда получаем систему обыкновенных дифференциальных уравнений
,
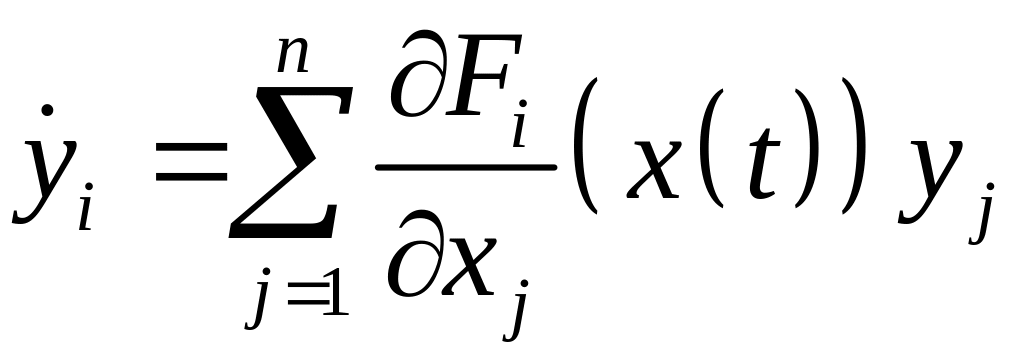(5)
определяющих динамику возмущений. Компактно имеем
,
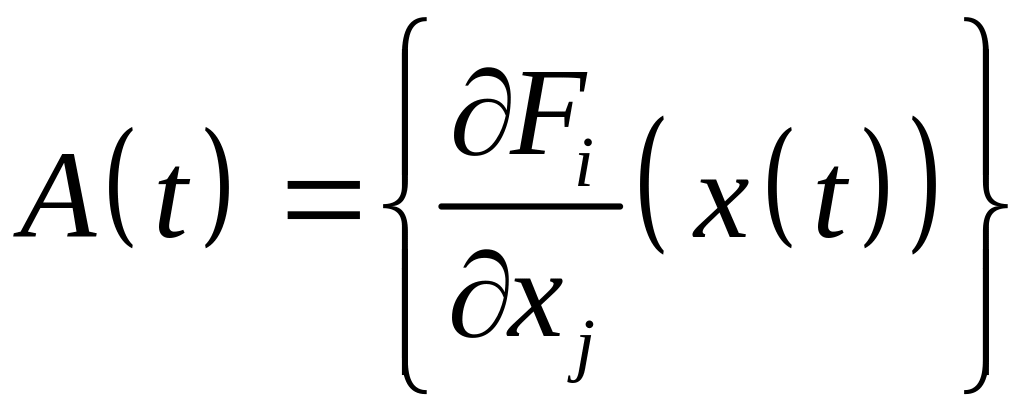. (6)
В
силу периодичности вектор-функции
матрица линеаризации
будет периодической функцией
.
(7)
Обозначим
вектор-столбцы фундаментальной системы
решений (6) через
.
Составим из этих столбцов фундаментальную
матрицу-решение
.
Данная матрица удовлетворяет следующему
уравнению
.
(8)
Имеем
.
(9)
Отсюда
видно, что матрица
также является фундаментальной
матрицей-решением. Отсюда вытекает, что
отличается от
постоянным «множителем» - неособенной
матрицей
,
не зависящей от времени
.
(10)
Матрица
называется матрицей монодромии.
Собственные значения
называются мультипликаторами. Обозначим
их через
.
Рассмотрим следующую задачу Коши
.
(11)
Здесь
- единичная матрица. Матрица
удовлетворяет соотношению (10):
.
(12)
Положим
в (12)
,
тогда получим
.
(13)
Т.о.,
матрица монодромии появляется из решения
задачи Коши (11), в котором следует положить
.
Мультипликаторы являются СЗ матрицы
:
.
(14)
Далее имеем
.
(15)
Так как является еще и фундаментальной матрицей-решением, то имеем
.
(16)
Отсюда последовательно находим
(17)
.
Далее получаем
(18)
Отсюда определяется функциональное уравнение, которому удовлетворяет :
(19)
Легко видеть, что (19) имеет решение
.
(20)
Величину
наз. показателем Флоке.
Показатели Флоке можно определить из решения задачи Коши
(21)
Решение этой задачи Коши имеет вид
,
(22)
что проверяется непосредственно при подстановке (22) в (21).
Далее имеем
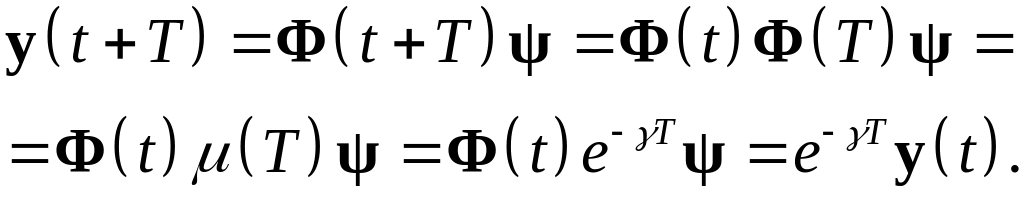(23)
Рассмотрим вектор-функцию
.
(24)
Она удовлетворяет условию периодичности
.
(25)
Дифференцируя (24), получим
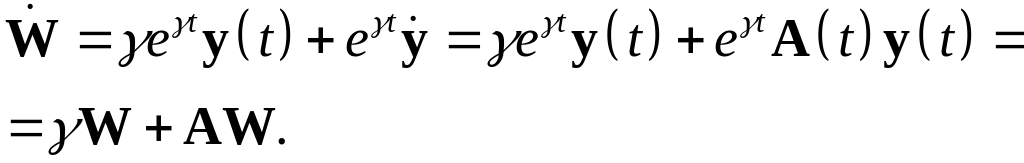(26)
Т.о., получаем следующую задачу на собственные значения
.
(27)
Показатели Флоке определяются как СЗ данной задачи.
Если
,
то возмущения нарастают - неустойчивость.
Если же
,
то возмущения не нарастают – устойчивость.
Выполняется также следующая теорема:
Физическая
система с
степенями свободы, описываемая линейным
дифференциальным уравнением порядка
с периодическими коэффициентами с
периодом
,
имеет
линейно независимых решений, образующих
фундаментальную систему, причем каждое
из этих решений имеет вид
,
(28)
где
.
(29)
Названия
- показатели Ляпунова,
-
ляпуновские экспоненты
- функции Флоке.