Современные проблемы физики / PhysicalReviewpdf / Tirskiy-2

-© нЛТНЛИ Й.А., 2001

SIMILARITY AND PHYSICAL MODELING

G. A. TIRSKIY

The mathematical rules of physical simulation of natural phenomena (processes) are described with the help of models. The both necessary and sufficient conditions of similarity of two phenomena are established, in model and in nature. It is shown how to use these conditions to design natural objects with given parameters, or to predict and study natural phenomena. The examples of using the rule of simulation are given. School education is sufficient to understand the material.

аБОУКВМ˚ П‡ЪВП‡ЪЛ˜ВТНЛВ Ф ‡‚ЛО‡ ЩЛБЛ- ˜ВТНУ„У ПУ‰ВОЛ У‚‡МЛfl М‡ЪЫ М˚ı fl‚ОВМЛИ (Ф УˆВТТУ‚) М‡ ПУ‰ВОflı. мТЪ‡МУ‚ОВМ˚ МВУ·- ıУ‰ЛП˚В Л ‰УТЪ‡ЪУ˜М˚В ЫТОУ‚Лfl ФУ‰У·Лfl ‰‚Ыı fl‚ОВМЛИ ‚ ПУ‰ВОЛ Л М‡ЪЫ В Л ФУН‡Б‡МУ, Н‡Н ЛПЛ ФУО¸БУ‚‡Ъ¸Тfl ‰Оfl Ф УВНЪЛ У‚‡МЛfl М‡ЪЫ М˚ı У·˙ВНЪУ‚ Т Б‡‰‡ММ˚ПЛ Ф‡ ‡ПВЪ-‡ПЛ ЛОЛ ‰Оfl Ф В‰ТН‡Б‡МЛfl Л ЛТТОВ‰У‚‡МЛfl fl‚ОВМЛИ М‡ЪЫ М˚ı Ф УˆВТТУ‚. С‡М˚ Ф ЛПВ-˚ Ф ЛПВМВМЛfl Ф ‡‚ЛО‡ ПУ‰ВОЛ У‚‡МЛfl. СОfl ФУМЛП‡МЛfl П‡ЪВ Л‡О‡ ‰УТЪ‡ЪУ˜МУ ¯НУО¸МУ„У У· ‡БУ‚‡МЛfl.

www.issep.rssi.ru

ЗЗЦСЦзаЦ

д‡НУИ П‡О¸˜ЛН МВ ТЪ УЛО ПУ‰ВОВИ Т‡ПУОВЪУ‚, НУ ‡·- ОВИ, ФОУЪЛМ Л ‚У‰УТОЛ‚У‚? зУ ‰‡КВ ‚Б УТО˚В Л УФ˚Ъ- М˚В ЛМКВМВ ˚-НУМТЪ ЫНЪУ ˚, Ф ВК‰В ˜ВП ЛБ„УЪУ‚ЛЪ¸ Н ЫФМУВ Л ‰У У„УТЪУfl˘ВВ ТУУ ЫКВМЛВ, М‡Ф ЛПВ ‚˚ТУНЫ˛ ЪВОВ·‡¯М˛, ФУ‰‚У‰МЫ˛ ОУ‰НЫ ЛОЛ ТЛТЪВПЫ ЪВФОУБ‡˘ЛЪ˚ НУТПЛ˜ВТНЛı ‡ФФ‡ ‡ЪУ‚, ‰Оfl ФУОЫ˜ВМЛfl Лı М‡ЛОЫ˜¯Лı (УФЪЛП‡О¸М˚ı) ı‡ ‡НЪВ ЛТЪЛН ‚ В‡О¸М˚ı ЫТОУ‚Лflı ‡·УЪ˚ Ф Л·В„‡˛Ъ ТМ‡˜‡О‡ Н ˝НТФВ ЛПВМЪ‡П М‡ ПУ‰ВОflı – ПУ‰ВОЛ У‚‡МЛ˛. и Л ˝ЪУП ‚ ˝НТФВ ЛПВМЪВ М‡ ПУ‰ВОflı ЛБПВ fl˛Ъ, М‡Ф ЛПВ , ‚ ‡˝ У‰ЛМ‡ПЛ˜ВТНЛı Ъ Ы·‡ı ТЛОЫ ТУФ УЪЛ‚ОВМЛfl Т‡ПУОВЪУ‚, ‚ ТЪ Ыflı ФО‡БПУЪ УМУ‚ ЪВФОУ‚˚В ФУЪУНЛ Н ЪВО‡П, М‡ Ф ВТТ‡ı М‡- „ ЫБНЛ, ‡Б Ы¯‡˛˘ЛВ ПУ‰ВОЛ ПУТЪУ‚, Л Ъ.Ф. н‡НЛВ ˝НТФВ ЛПВМЪ˚ М‡ ПУ‰ВОflı ·Ы‰ЫЪ ТУ‰В К‡ЪВО¸М˚ПЛ Л ФУОВБМ˚ПЛ ‰Оfl Ф УВНЪЛ У‚‡МЛfl М‡ЪЫ М˚ı У·˙ВНЪУ‚, ВТОЛ УМЛ Ф У‚У‰flЪТfl Т ТУ·О˛‰ВМЛВП УФ В‰ВОВММ˚ı Ф ‡‚ЛО ПУ‰ВОЛ У‚‡МЛfl. З Ф УЪЛ‚МУП ТОЫ˜‡В ВБЫО¸Ъ‡Ъ˚ ˝НТФВ-ЛПВМЪУ‚ Ф В‰ТЪ‡‚Оfl˛Ъ ТУ·УИ М‡·У П‡ОУТУ‰В К‡ЪВО¸- М˚ı Щ‡НЪУ‚, ·ВТФУОВБМ˚ı ‰Оfl Ф УВНЪЛ У‚‡МЛfl МУ‚˚ı М‡ЪЫ М˚ı У·˙ВНЪУ‚.

оЛБЛ˜ВТНУВ ПУ‰ВОЛ У‚‡МЛВ ‚ УЪОЛ˜ЛВ УЪ П‡ЪВП‡- ЪЛ˜ВТНУ„У – ˝ЪУ Б‡ПВМ‡ ЛБЫ˜ВМЛfl ЛМЪВ ВТЫ˛˘В„У М‡Т fl‚ОВМЛfl, Ф УЪВН‡˛˘В„У ‚ М‡ЪЫ В, ЛБЫ˜ВМЛВП ‡М‡ОУ„Л˜- МУ„У (ФУ‰У·МУ„У) fl‚ОВМЛfl М‡ ПУ‰ВОЛ, Н‡Н Ф ‡‚ЛОУ, ПВМ¸¯В„У ЛОЛ ·УО¸¯В„У ‡БПВ ‡ (ЛОЛ, ‰ Ы„ЛПЛ ТОУ‚‡- ПЛ, М‡ ПУ‰ВОЛ ТУ БМ‡˜ВМЛflПЛ УФ В‰ВОfl˛˘Лı Ф‡ ‡ПВЪ-У‚ ˝ЪУ„У fl‚ОВМЛfl, Ы‰У·МУ ‰УТЪЛКЛП˚ПЛ ‚ ˝НТФВ Л- ПВМЪВ) У·˚˜МУ ‚ ТФВˆЛ‡О¸М˚ı О‡·У ‡ЪУ М˚ı ЫТОУ‚Лflı. йТМУ‚МУИ ТП˚ТО ПУ‰ВОЛ У‚‡МЛfl Б‡НО˛˜‡ВЪТfl ‚ ЪУП, ˜ЪУ·˚ ФУ ВБЫО¸Ъ‡Ъ‡П УФ˚ЪУ‚ Т ПУ‰ВОflПЛ, НУЪУ ˚В Ы‰У·МУ Л Т ПВМ¸¯ЛПЛ Б‡Ъ ‡Ъ‡ПЛ Т В‰ТЪ‚ Л ‚ ВПВМЛ ЛБ- „УЪУ‚ЛЪ¸, ПУКМУ ·˚ОУ ЫН‡Б‡Ъ¸ М‡ЛОЫ˜¯ЛВ ı‡ ‡НЪВ ЛТЪЛНЛ М‡ЪЫ МУ„У ЛБ‰ВОЛfl (Ф УˆВТТ‡), ‡ ЛМУ„‰‡ Ф УТЪУ ЫТ- Ъ‡МУ‚ЛЪ¸ МВЛБ‚ВТЪМ˚В ‡МВВ Б‡НУМУПВ МУТЪЛ.

мТЪ‡МУ‚ОВМЛВ ЛТНУП˚ı Б‡НУМУПВ МУТЪВИ Т ФУПУ- ˘¸˛ ЩЛБЛ˜ВТНУ„У ПУ‰ВОЛ У‚‡МЛfl Б‡˜‡ТЪЫ˛ fl‚ОflВЪТfl В‰ЛМТЪ‚ВММУ ‚УБПУКМ˚П ТФУТУ·УП ˝НТФВ ЛПВМЪ‡О¸- МУ„У ЛБЫ˜ВМЛfl Л В¯ВМЛfl ‚‡КМ˚ı Л МЫКМ˚ı Ф ‡НЪЛ˜В- ТНЛı Б‡‰‡˜. н‡Н У·ТЪУЛЪ ‰ВОУ Ф Л ЛБЫ˜ВМЛЛ Ф Л У‰М˚ı fl‚ОВМЛИ, „‰В Ф УˆВТТ˚ ·˚‚‡˛Ъ МВУ·˚˜‡ИМУ ТОУКМ˚ Л Ф УЪВН‡˛Ъ ‚ ЪВ˜ВМЛВ ‰ВТflЪНУ‚, ТУЪВМ ЛОЛ ‰‡КВ Ъ˚Тfl˜

ОВЪ. З ЫТОУ‚Лflı ПУ‰ВО¸М˚ı УФ˚ЪУ‚ ФУ‰У·МУВ fl‚ОВМЛВ ПУКВЪ Ф У‰УОК‡Ъ¸Тfl ‚ТВ„У МВТНУО¸НУ ˜‡ТУ‚ ЛОЛ ‰МВИ. л ˝ЪЛП П˚ ‚ТЪ В˜‡ВПТfl Ф Л ПУ‰ВОЛ У‚‡МЛЛ fl‚ОВМЛИ Ф У- Т‡˜Л‚‡МЛfl МВЩЪЛ, ‡Б ‡·‡Ъ˚‚‡ВПУИ Л УЪН‡˜Л‚‡ВПУИ ˜В ВБ ТН‚‡КЛМ˚, Ъ‡flМЛfl Л ТФУОБ‡МЛfl ОВ‰МЛНУ‚ Л ‰ . еУ„ЫЪ ·˚Ъ¸ Л У· ‡ЪМ˚В ТОЫ˜‡Л, НУ„‰‡ ‚ПВТЪУ ЛТТОВ‰У- ‚‡МЛfl У˜ВМ¸ ·˚ТЪ У Ф УЪВН‡˛˘В„У ‚ Ф Л У‰В fl‚ОВМЛfl ПУКМУ ˝НТФВ ЛПВМЪ‡О¸МУ ЛБЫ˜‡Ъ¸ ФУ‰У·МУВ ВПЫ fl‚ОВМЛВ, Ф УЛТıУ‰fl˘ВВ М‡ ПУ‰ВОЛ „У ‡Б‰У ПВ‰ОВММВВ. еУ- ‰ВОЛ У‚‡МЛВ Т ЫТФВıУП Ф ЛПВМflВЪТfl ‚ ‡Б ‡·УЪНВ МУ- ‚˚ı ЪЛФУ‚ Т‡ПУОВЪУ‚, НУТПЛ˜ВТНУИ ЪВıМЛНЛ, ТУБ‰‡МЛЛ fl‰В МУ„У У ЫКЛfl, НУ ‡·ОВТЪ УВМЛЛ, ‡‚ЪУПУ·ЛОВТЪ УВМЛЛ, ·ЛУПВı‡МЛНВ, УНВ‡МУОУ„ЛЛ, ПВЪВУ УОУ„ЛЛ, ‡ТЪ У- ЩЛБЛНВ, М‡ЫНВ У бВПОВ Л ФО‡МВЪ‡ı Л ‚У ПМУ„Лı ‰ Ы„Лı У·О‡ТЪflı ˜ВОУ‚В˜ВТНУИ ‰ВflЪВО¸МУТЪЛ [1–5].

оЛБЛ˜ВТНУВ ПУ‰ВОЛ У‚‡МЛВ – УЪ‚ВЪТЪ‚ВММ‡fl М‡Ы˜- М‡fl Б‡‰‡˜‡, ЛПВ˛˘‡fl У·˘ВВ Ф ЛМˆЛФЛ‡О¸МУВ Л ФУБМ‡- ‚‡ЪВО¸МУВ БМ‡˜ВМЛВ. йМУ УТМУ‚˚‚‡ВЪТfl М‡ „ОЫ·УНУП Ф УМЛНМУ‚ВМЛЛ ‚ fl‚ОВМЛВ (‚ Ф УˆВТТ), ‚ ‡Б ‡·УЪНЫ ˝НТФВ ЛПВМЪ‡О¸М˚ı Л ЪВУ ВЪЛ˜ВТНЛı ПВЪУ‰У‚ ЛТТОВ‰У- ‚‡МЛfl ‰Оfl ФУОЫ˜ВМЛfl ‰УТЪУ‚В М˚ı ВБЫО¸Ъ‡ЪУ‚ Л ‚ ЛЪУ„В ФУОЫ˜ВМЛfl ТЛТЪВП‡ЪЛ˜ВТНЛı Ф ‡‚ЛО Л ВНУПВМ‰‡ˆЛИ ‰Оfl В¯ВМЛfl НУМН ВЪМ˚ı Ф ‡НЪЛ˜ВТНЛı Б‡‰‡˜. АО¸- ЪВ М‡ЪЛ‚УИ ЩЛБЛ˜ВТНУПЫ ПУ‰ВОЛ У‚‡МЛ˛ fl‚ОflВЪТfl П‡- ЪВП‡ЪЛ˜ВТНУВ ПУ‰ВОЛ У‚‡МЛВ, Ф Л‚В‰¯ВВ ‚ ФУТОВ‰МЛВ ‰ВТflЪЛОВЪЛfl XX ‚ВН‡ Н ФУ‰ОЛММУ В‚УО˛ˆЛУММУПЫ Ф ВУ· ‡БУ‚‡МЛ˛ М‡ЫНЛ ‚УУ·˘В Л П‡ЪВП‡ЪЛНЛ ‚ УТУ·ВММУТЪЛ Л „‡ ПУМЛ˜МУ ‰УФУОМfl˛˘ВВ ЩЛБЛ˜ВТНУВ ПУ‰В- ОЛ У‚‡МЛВ. е‡ЪВП‡ЪЛ˜ВТНУВ ПУ‰ВОЛ У‚‡МЛВ – ˝ЪУ, Н‡Н Ф ‡‚ЛОУ, ˜ЛТОВММУВ В¯ВМЛВ М‡ щЗе ‡О„В· ‡Л˜ВТНЛı, ‰ЛЩЩВ ВМˆЛ‡О¸М˚ı ЛОЛ ЛМЪВ„ ‡О¸М˚ı Ы ‡‚МВМЛИ, ‚˚- ЪВН‡˛˘Лı ЛБ Ф ЛПВМВМЛfl Б‡НУМУ‚ ПВı‡МЛНЛ, ЩЛБЛНЛ, ıЛПЛЛ, ·ЛУОУ„ЛЛ, ˝НУМУПЛНЛ Н В¯ВМЛ˛ НУМН ВЪМ˚ı Б‡‰‡˜ [6].

СОfl Ф ‡‚ЛО¸МУ„У ЩЛБЛ˜ВТНУ„У ПУ‰ВОЛ У‚‡МЛfl МВ- У·ıУ‰ЛПУ, ‚У-ФВ ‚˚ı, ЫТЪ‡МУ‚ЛЪ¸ ЫТОУ‚Лfl ФУ‰У·Лfl ‰‚Ыı fl‚ОВМЛИ – ‚ ПУ‰ВОЛ Л М‡ЪЫ В Л, ‚У-‚ЪУ ˚ı, УФ В‰В- ОЛЪ¸, Н‡Н ЛПЛ ФУО¸БУ‚‡Ъ¸Тfl ‰Оfl Ф УВНЪЛ У‚‡МЛfl М‡ЪЫ - М˚ı У·˙ВНЪУ‚ Т Б‡‰‡ММ˚ПЛ Ф‡ ‡ПВЪ ‡ПЛ ЛОЛ Ф В‰ТН‡- Б‡МЛfl fl‚ОВМЛИ М‡ЪЫ М˚ı Ф УˆВТТУ‚. аТТОВ‰У‚‡ЪВОflП, Н‡Н ЪВУ ВЪЛН‡П, Ъ‡Н Л ˝НТФВ ЛПВМЪ‡ЪУ ‡П, ФУОВБМУ БМ‡Ъ¸, ˜ЪУ ПУ„ЫЪ ‰‡Ъ¸ ПВЪУ‰˚ ФУ‰У·Лfl Л Н‡Н ЛПЛ ФУО¸- БУ‚‡Ъ¸Тfl. й· ˝ЪУП М‡¯‡ ТЪ‡Ъ¸fl.

ийСйЕзхЦ ьЗгЦзаь

иУМflЪЛВ ПВı‡МЛ˜ВТНУ„У ЛОЛ ЩЛБЛ˜ВТНУ„У ФУ‰У·Лfl ПУКМУ ‡ТТП‡Ъ Л‚‡Ъ¸ Н‡Н У·У·˘ВМЛВ „ВУПВЪ Л˜ВТНУ„У ФУ‰У·Лfl, ıУ У¯У ЛБ‚ВТЪМУ„У ЛБ ¯НУО¸МУ„У НЫ Т‡ „ВУПВЪ ЛЛ. т „ВУПВЪ Л˜ВТНЛВ ЩЛ„Ы ˚ ФУ‰У·М˚, ВТОЛ УЪМУ¯ВМЛfl ‚ТВı ТУУЪ‚ВЪТЪ‚Ы˛˘Лı ‰ОЛМ У‰ЛМ‡НУ‚˚, ‡ ·ВБ ‡БПВ М˚В Ф‡ ‡ПВЪ ˚ – Ы„О˚ Ф Л ТУУЪ‚ВЪТЪ‚Ы˛˘Лı ‚В ¯ЛМ‡ı – ‰Оfl У·ВЛı ЩЛ„Ы ‡‚М˚.

СОfl НУОЛ˜ВТЪ‚ВММУ„У УФ В‰ВОВМЛfl ЩЛБЛ˜ВТНУ„У ФУ‰У·Лfl ‚В МВПТfl Н ‡М‡ОЛБЫ ‡БПВ МУТЪВИ Л Н ‡ЪНУ ТЩУ ПЫОЛ ЫВП В„У „О‡‚М˚И ВБЫО¸Ъ‡Ъ [7]. иЫТЪ¸ Л˘ВЪТfl (ЛПВВЪТfl, ФУ‰УБ В‚‡ВЪТfl) Н‡Н‡fl-ОЛ·У Б‡‚ЛТЛПУТЪ¸, УФ-В‰ВОfl˛˘‡fl ЛТНУПЫ˛ ‚ВОЛ˜ЛМЫ a ‚ ÙÛÌ͈ËË n ÓÔ Â‰Â- Îfl˛˘Ëı Ô‡ ‡ÏÂÚ Ó‚ a1 , a2 , …, an :

ЦТОЛ ˝Ъ‡ Б‡‚ЛТЛПУТЪ¸ ‚˚ ‡К‡ВЪ МВНУЪУ Ы˛ ЩЛБЛ˜ВТНЫ˛ Б‡НУМУПВ МУТЪ¸, ЪУ УМ‡ ‰УОКМ‡ УЪ ‡К‡Ъ¸ ЪУЪ ·ВТТФУ М˚И Щ‡НЪ, ˜ЪУ ЩЫМНˆЛfl (1) МВ ‰УОКМ‡ Б‡‚ЛТВЪ¸ УЪ Ф УЛБ‚УО‡ ‚˚·У ‡ В‰ЛМЛˆ ЛБПВ ВМЛfl. СОfl ФУОЫ˜ВМЛfl ТОВ‰ТЪ‚Лfl ЛБ ˝ЪУ„У Щ‡НЪ‡ ‡БУ·¸ВП Ф‡ ‡ПВЪ ˚ a, a1 , a2 , …, an ̇ ‰‚ „ ÛÔÔ˚, Í‡Í ˝ÚÓ Ò‰Â·ÌÓ ‚ (1). Ç Ô ‚Û˛ „ ÛÔÔÛ (a1 , a2 , …, ak ; k # n) ‚НО˛˜‡˛ЪТfl ‚ВОЛ˜ЛМ˚ Т МВ- Б‡‚ЛТЛП˚ПЛ ‡БПВ МУТЪflПЛ (М‡Ф ЛПВ , МВНУЪУ ‡fl ‰ОЛ- М‡, ТНУ УТЪ¸, ФОУЪМУТЪ¸ Л Ъ.‰.); ‚У ‚ЪУ Ы˛ „ ЫФФЫ (a, ak + 1, ak + 2 , …, an) ‚ıУ‰flЪ УТЪ‡О¸М˚В Ф‡ ‡ПВЪ ˚ Т ‡БПВ МУТЪflПЛ, ‚˚ ‡К‡ВП˚ПЛ ˜В ВБ ‡БПВ МУТЪЛ ‚ВОЛ˜ЛМ ФВ ‚УИ „ ЫФФ˚. нУ„‰‡ ‡БПВ МУТЪЛ ‚ВОЛ˜ЛМ a, ak + 1 , …, an ·Ы‰ЫЪ ‚˚ ‡К‡Ъ¸Тfl ‚ ‚Л‰В Ф УЛБ‚В‰ВМЛИ ТЪВФВМВИ УЪ ‡БПВ - МУТЪВИ Ф‡ ‡ПВЪ У‚ a1 , a2 , …, ak :

лЪВФВМЛ α, β, …, γ ФУОЫ˜‡˛ЪТfl Т ‡‚МВМЛВП ‡БПВ МУТЪВИ ОВ‚˚ı Л Ф ‡‚˚ı ˜‡ТЪВИ ‚ (2). и Л ˝ЪУП ‚ВОЛ˜ЛМ˚, Н‡Н ОВ„НУ ЫТЪ‡МУ‚ЛЪ¸,

УН‡Б˚‚‡˛ЪТfl ·ВБ ‡БПВ М˚ПЛ (˜ЛТОЛЪВОЛ Л БМ‡ПВМ‡ЪВОЛ ‚ МЛı ЛПВ˛Ъ У‰ЛМ‡НУ‚˚В ‡БПВ МУТЪЛ), ЪУ ВТЪ¸ Лı БМ‡˜ВМЛfl ·Ы‰ЫЪ У‰МЛПЛ Л ЪВПЛ КВ Ф Л О˛·УП ‚˚·У В В‰ЛМЛˆ ЛБПВ ВМЛfl.

аБ МВБ‡‚ЛТЛПУТЪЛ ЩЛБЛ˜ВТНУИ Б‡НУМУПВ МУТЪЛ (1) УЪ ‚˚·У ‡ В‰ЛМЛˆ ЛБПВ ВМЛfl ‚˚ЪВН‡ВЪ, ˜ЪУ ТУУЪ‚ВЪТЪ- ‚Ы˛˘ВВ ВИ ТУУЪМУ¯ВМЛВ ПУКМУ Ф В‰ТЪ‡‚ЛЪ¸ ‚ ‚Л‰В Б‡-

‚ЛТЛПУТЪЛ ЪУО¸НУ ПВК‰Ы ·ВБ ‡БПВ М˚ПЛ Ф‡ ‡ПВЪ ‡ПЛ

(Π = f ⁄ (aα1 aβ2 …aγk )) [7]

ЪУ ВТЪ¸ ЛТНУП‡fl ЩЫМНˆЛfl М‡ Т‡ПУП ‰ВОВ ‚ТВ„‰‡ ПУКВЪ ·˚Ъ¸ Ф В‰ТЪ‡‚ОВМ‡ ˜В ВБ ЩЫМНˆЛ˛ ПВМ¸¯В„У ˜ЛТО‡ ·ВБ-‡БПВ М˚ı ‡ „ЫПВМЪУ‚. уЛТОУ ‡ „ЫПВМЪУ‚ ‚ (4) ПВМ¸¯В ЛТıУ‰МУ„У ˜ЛТО‡ n ̇ ÒÚÓθÍÓ, ÒÍÓθÍÓ Ò Â‰Ë ‚Â΢ËÌ a1 , a2 , …, an ЛПВВЪТfl ‚ВОЛ˜ЛМ Т МВБ‡‚ЛТЛП˚ПЛ ‡БПВ - МУТЪflПЛ. мПВМ¸¯ВМЛВ ˜ЛТО‡ ‡ „ЫПВМЪУ‚ ЫФ У˘‡ВЪ ЛТТОВ‰У‚‡МЛВ, ЛМУ„‰‡ ТЫ˘ВТЪ‚ВММУ. и Л‚В‰ВМЛВ ЛТНУПУИ Б‡НУМУПВ МУТЪЛ Н ·ВБ ‡БПВ МУПЫ ‚Л‰Ы (4) М‡Б˚‚‡ВЪТfl ÔË-ÚÂÓ ÂÏÓÈ (Π-ÚÂÓ Âχ). нВФВ ¸ ПУКМУ НУОЛ˜ВТЪ‚ВММУ УФ В‰ВОЛЪ¸ ФУМflЪЛВ ЩЛБЛ˜ВТНУ„У ФУ‰У·Лfl fl‚ОВМЛИ.

СОfl ЩЛБЛ˜ВТНУ„У ФУ‰У·Лfl ‰‚Ыı „ВУПВЪ Л˜ВТНЛ ФУ- ‰У·М˚ı fl‚ОВМЛИ МВУ·ıУ‰ЛПУ Л ‰УТЪ‡ЪУ˜МУ, ˜ЪУ·˚ УМЛ УФ В‰ВОflОЛТ¸ У‰МЛП Л ЪВП КВ М‡·У УП УФ В‰ВОfl˛˘Лı Ф‡ ‡ПВЪ У‚ a1 , a2 , …, an , ˜ЛТОВММ˚В БМ‡˜ВМЛfl НУЪУ ˚ı ПУ„ЫЪ УЪОЛ˜‡Ъ¸Тfl ‚ ˝ЪЛı fl‚ОВМЛflı, МУ Ф ЛЪУП Ъ‡Н, ˜ЪУ ˜ЛТОВММ˚В БМ‡˜ВМЛfl ·ВБ ‡БПВ М˚ı Ф‡ ‡ПВЪ У‚ Πk + 1 , … …, Πn ТУ‚Ф‡‰‡˛Ъ ‚ ˝ЪЛı fl‚ОВМЛflı. З Т‚flБЛ Т Ф ЛМflЪ˚П УФ В‰ВОВМЛВП ФУ‰У·М˚ı fl‚ОВМЛИ Ф‡ ‡ПВЪ ˚ Πk + 1 , … …, Πn ̇Á˚‚‡˛ÚÒfl Ô‡ ‡ÏÂÚ ‡ÏË ÔÓ‰Ó·Ëfl.

аЪ‡Н, Ф Л ФУ‰У·ЛЛ ‰‚Ыı fl‚ОВМЛИ, НУЪУ ˚В П˚ ·Ы- ‰ВП ‰‡ОВВ М‡Б˚‚‡Ъ¸ У‰МУ М‡ЪЫ М˚П Л ‰ Ы„УВ ПУ‰ВО¸- М˚П, УФ В‰ВОflВП‡fl ‚ВОЛ˜ЛМ‡ a ‰УОКМ‡ ЛПВЪ¸ У‰ЛМ‡НУ- ‚Ы˛ ЩЫМНˆЛУМ‡О¸МЫ˛ Б‡‚ЛТЛПУТЪ¸ УЪ УФ В‰ВОfl˛˘Лı Ф‡ ‡ПВЪ У‚ a1 , a2 , …, ak , ak + 1 , …, an (1). íÓ ÂÒÚ¸ ÙÛÌ͈Ëfl f ‰Оfl У·УЛı fl‚ОВМЛИ ·Ы‰ВЪ У‰М‡ Л Ъ‡ КВ, ФУТНУО¸НЫ fl‚ОВМЛfl ФУ‰У·М˚, ıУЪfl ˜ЛТОВММ˚В БМ‡˜ВМЛfl УФ В‰ВОfl˛˘Лı Ф‡ ‡ПВЪ У‚ Л УФ В‰ВОflВПУИ ЩЛБЛ˜ВТНУИ ‚ВОЛ˜ЛМ˚ a ПУ„ЫЪ ‡БОЛ˜‡Ъ¸Тfl. иУ˝ЪУПЫ ‰Оfl М‡ЪЫ МУ„У fl‚ОВМЛfl ЛТНУП‡fl Б‡‚ЛТЛПУТЪ¸ (1) Ф ЛМЛП‡ВЪ ‚Л‰

б‰ВТ¸ ‚В ıМЛВ ЛМ‰ВНТ˚ (М) Л (П) УЪМУТflЪТfl ТУУЪ‚ВЪТЪ- ‚ВММУ Н М‡ЪЫ В Л ПУ‰ВОЛ. и ЛПВМflfl Π-ЪВУ ВПЫ, У·В Б‡- ‚ЛТЛПУТЪЛ (6) Л (7) ПУКВП ФВ ВФЛТ‡Ъ¸ ‚ ·ВБ ‡БПВ МУП ‚Л‰В (ТП. (4))

Π(Ì) = Φ(Π(kÌ+)1, …, Π(nÌ)),

(8)

Π(Ï) = Φ(Π(kÏ+)1, …, Π(nÏ)).

и Л˜ВП ‚‡КМУ УЪПВЪЛЪ¸, ˜ЪУ Б‰ВТ¸ ЩЫМНˆЛfl Φ ‰Оfl М‡ЪЫ-˚ Л ПУ‰ВОЛ У‰М‡ Л Ъ‡ КВ, Ъ‡Н Н‡Н УМ‡ ‚ У·УЛı ТОЫ˜‡flı У‰ЛМ‡НУ‚У ‚˚ ‡К‡ВЪТfl ˜В ВБ У‰МЫ Л ЪЫ КВ ЩЫМНˆЛ˛ f (ÒÏ. (5)).

икАЗагй иЦкЦлуЦнА йихнйЗ л ийСйЕзйв ейСЦга зА зАнмкм

ЦТОЛ ЫТОУ‚Лfl ФУ‰У·Лfl ‚˚ФУОМВМ˚, ЪУ ‰УОКМ˚ ‚˚ФУОМflЪ¸Тfl ‡‚ВМТЪ‚‡

щЪЛ ЫТОУ‚Лfl ЛМУ„‰‡ ЛПВМЫ˛Ъ Í ËÚ ËflÏË ÔÓ‰Ó·Ëfl. ëÎÂ- ‰Ó‚‡ÚÂθÌÓ, Ò Û˜ÂÚÓÏ (9) ËÁ (4) ÔÓÎÛ˜‡ÂÏ ‡‚ÂÌÒÚ‚Ó ·ÂÁ-‡ÁÏ ÌÓÈ ÓÔ Â‰ÂÎflÂÏÓÈ ‚Â΢ËÌ˚ ‰Îfl ÏÓ‰ÂÎË Ë Ì‡ÚÛ ˚

ЗУБ‚ ‡˘‡flТ¸ УЪ ‡‚ВМТЪ‚‡ (10) У· ‡ЪМУ Н ‡БПВ М˚П ФВ ВПВММ˚П a, a1, …, ak , Т Ы˜ВЪУП ФВ ‚УИ ЩУ ПЫО˚ (3) ФУОЫ˜ЛП Ф УТЪУВ Ф ‡‚ЛОУ ФВ ВТ˜ВЪ‡ ВБЫО¸Ъ‡ЪУ‚ ЛБПВ-ВМЛИ Т ФУ‰У·МУ„У ПУ‰ВО¸МУ„У fl‚ОВМЛfl М‡ М‡ЪЫ МУВ fl‚- ОВМЛВ ‚ ‚Л‰В

ЗТВ, ˜ЪУ ТЪУЛЪ ТФ ‡‚‡ ‚ (11) ФУТОВ a(Ï), ˜‡ÒÚÓ Ì‡Á˚‚‡˛Ú Ô ÂıÓ‰Ì˚Ï Ï‡Ò¯Ú‡·ÓÏ. ÑÎfl k ‚Â΢ËÌ Ò ÌÂÁ‡‚ËÒËÏ˚- ÏË ‡ÁÏ ÌÓÒÚflÏË a1 , a2 , …, ak ФВ ВıУ‰М˚В П‡Т¯Ъ‡·˚ ПУ„ЫЪ ·˚Ъ¸ Ф УЛБ‚УО¸М˚ПЛ, Л Лı МЫКМУ Б‡‰‡‚‡Ъ¸ ЛОЛ УФ В‰ВОflЪ¸ ЫТОУ‚ЛflПЛ Б‡‰‡˜Л, ‡ Ф Л ˝НТФВ ЛПВМЪ‡ı – ЛБ УФ˚ЪУ‚, ЛПВfl ‚ ‚Л‰Ы ФУОЫ˜ВМЛВ П‡НТЛП‡О¸МУИ Ф У- ТЪУЪ˚ Л Ы‰У·ТЪ‚У ПУ‰ВОЛ У‚‡МЛfl. иВ ВıУ‰М˚В П‡Т¯Ъ‡- ·˚ ‰Оfl ‚ТВı КВ УТЪ‡О¸М˚ı ‡БПВ М˚ı ‚ВОЛ˜ЛМ ak + 1 , … …, an ‰Оfl У·ВТФВ˜ВМЛfl ФУ‰У·Лfl ПУ‰ВОЛ М‡ЪЫ В ФУОЫ˜‡- ˛ЪТfl ЛБ ЫТОУ‚ЛИ (9) Т ЛТФУО¸БУ‚‡МЛВП ЩУ ПЫО (3):

и Л‚В‰ВММ˚В ‚˚¯В Ф УТЪ˚В УФ В‰ВОВМЛfl Л ЫЪ- ‚В К‰ВМЛfl ФУОМУТЪ¸˛ ЛТ˜В Ф˚‚‡˛Ъ ТУ‰В К‡МЛВ ЪВУ-ЛЛ ФУ‰У·Лfl: МЛ˜В„У ‰ Ы„У„У ‚ ˝ЪУИ ЪВУ ЛЛ ·УО¸¯В МВЪ. й‰М‡НУ М‡ Ф ‡НЪЛНВ ˜‡ТЪУ ‚˚ФУОМВМЛВ ‚ТВı ЫТОУ‚ЛИ (9) У‰МУ‚ ВПВММУ ·˚‚‡ВЪ Б‡Ъ Ы‰МВМУ (УМЛ ‚ТВ„‰‡ ‚˚ФУОМfl- ˛ЪТfl, ВТОЛ ПУ‰ВО¸ ТУ‚Ф‡‰‡ВЪ Т М‡ЪЫ УИ, МУ ЪУ„‰‡ ПУ‰В- ОЛ У‚‡МЛВ ЪВ flВЪ ‚ТflНЛИ ТП˚ТО), Л ЪУ„‰‡ ‚ТЪ‡ВЪ ‚УФ УТ У ‚ВОЛ˜ЛМВ ФУ„ В¯МУТЪВИ (П‡Т¯Ъ‡·МУП ˝ЩЩВНЪВ), НУЪУ ˚В ‚УБМЛН‡˛Ъ Ф Л ФВ ВМУТВ М‡ М‡ЪЫ Ы ВБЫО¸Ъ‡ЪУ‚, ФУОЫ˜ВММ˚ı М‡ ПУ‰ВОЛ. б‰ВТ¸ ‚УБМЛН‡ВЪ Ф У·ОВП‡ Ф Л- ·ОЛКВММУ„У ПУ‰ВОЛ У‚‡МЛfl (ЛМУ„‰‡ ˜‡ТЪ¸ ·ВБ ‡БПВ - М˚ı Ф‡ ‡ПВЪ У‚ ТО‡·У ‚ОЛflВЪ М‡ ВБЫО¸Ъ‡Ъ, ЪУ„‰‡ ‚˚ФУОМВМЛВ МВНУЪУ ˚ı Н ЛЪВ ЛВ‚ (9) ПУКМУ Л„МУ Л У‚‡Ъ¸, ЛМУ„‰‡ Ф Л·В„‡˛Ъ Н ˜‡ТЪЛ˜МУПЫ ЛОЛ ОУН‡О¸МУПЫ ПУ‰В- ОЛ У‚‡МЛ˛, ЫТОУ‚Лfl ‰Оfl НУЪУ У„У УТО‡·ОВМ˚ ФУ Т ‡‚- МВМЛ˛ Т ЫТОУ‚ЛflПЛ ФУОМУ„У ПУ‰ВОЛ У‚‡МЛfl (9)).

икаеЦкх

1. ᇉ‡˜‡ У· УФ В‰ВОВМЛЛ ТУФ УЪЛ‚ОВМЛfl ЪВО‡, ‰‚Л- КЫ˘В„УТfl ФУТЪЫФ‡ЪВО¸МУ ‚ ·ВБ„ ‡МЛ˜МУИ ‚flБНУИ КЛ‰НУТЪЛ Т ФУТЪУflММУИ ТНУ УТЪ¸˛. к‡ТТПУЪ ЛП ‰‚ЛКВМЛВ ЪВО‡ Т ФУТЪУflММУИ ТНУ УТЪ¸˛ υ ‚ ‚flБНУИ МВТКЛП‡ВПУИ ·ВБ- „ ‡МЛ˜МУИ (Б‡МЛП‡˛˘ВИ У˜ВМ¸ ·УО¸¯УИ ФУ Т ‡‚МВМЛ˛

Т ЪВОУП У·˙ВП) КЛ‰НУТЪЛ, Т‚УИТЪ‚‡ НУЪУ УИ ‚ФУОМВ УФ-В‰ВОfl˛ЪТfl ФОУЪМУТЪ¸˛ ρ Л НУ˝ЩЩЛˆЛВМЪУП ‚flБНУТЪЛ µ. нВОУ-ПУ‰ВО¸ ‰УОКМУ ·˚Ъ¸ „ВУПВЪ Л˜ВТНЛ ФУ‰У·МУ ЪВ- ОЫ-М‡ЪЫ В; М‡Ф ‡‚ОВМЛВ ТНУ УТЪЛ ФУ УЪМУ¯ВМЛ˛ Н ТУУЪ‚ВЪТЪ‚Ы˛˘ЛП УТflП ЪВО‡ ‚ ПУ‰ВО¸МУП Л М‡ЪЫ МУП ‰‚ЛКВМЛflı ‰УОКМУ ·˚Ъ¸ У‰ЛМ‡НУ‚˚П (ЫТОУ‚ЛВ НЛМВ- П‡ЪЛ˜ВТНУ„У ФУ‰У·Лfl). щЪУ Ф Л‚У‰ЛЪ Н ‡‚ВМТЪ‚Ы ‰Оfl ПУ‰ВО¸МУ„У Л М‡ЪЫ МУ„У fl‚ОВМЛИ ТУУЪ‚ВЪТЪ‚Ы˛˘Лı „В- УПВЪ Л˜ВТНЛı Л НЛМВП‡ЪЛ˜ВТНЛı Ф‡ ‡ПВЪ У‚ ФУ‰У·Лfl. З Н‡˜ВТЪ‚В УФ В‰ВОfl˛˘В„У „ВУПВЪ Л˜ВТНУ„У ‡БПВ ‡ ‚УБ¸ПВП, М‡Ф ЛПВ , ‰Л‡ПВЪ В„У ФУФВ В˜МУ„У ТВ˜ВМЛfl d (ПЛ‰ВОfl). к‡БПВ МУТЪЛ УФ В‰ВОfl˛˘Лı Ф‡ ‡ПВЪ У‚ ‚ НО‡ТТВ LMT (‰ОЛМ‡, П‡ТТ‡, ‚ ВПfl)

[υ] = LT −1, [d] = L, [ρ] = ML−3, [µ] = ML−1T −1,

ÚÓ ÂÒÚ¸ n = 4, k = 3. лОВ‰У‚‡ЪВО¸МУ, ФУПЛПУ „ВУПВЪ Л- ˜ВТНЛı Л НЛМВП‡ЪЛ˜ВТНЛı Ф‡ ‡ПВЪ У‚ ФУ‰У·Лfl ЛПВВЪТfl ЪУО¸НУ У‰ЛМ ‰ЛМ‡ПЛ˜ВТНЛИ Ф‡ ‡ПВЪ ФУ‰У·Лfl, НУЪУ ˚И

иУ Ф В‰ОУКВМЛ˛ А. бУППВ ЩВО¸‰‡ ˝ЪУЪ Ф‡ ‡ПВЪ М‡- Б˚‚‡ВЪТfl Ф‡ ‡ПВЪ УП ЛОЛ ˜ЛТОУП кВИМУО¸‰Т‡ ‚ ˜ВТЪ¸ ‡М„- ОЛИТНУ„У ЛТТОВ‰У‚‡ЪВОfl й. кВИМУО¸‰Т‡, Ф ЛПВМЛ‚¯В„У У‰МЛП ЛБ ФВ ‚˚ı Л‰ВЛ ФУ‰У·Лfl ‚ „Л‰ У‰ЛМ‡ПЛНВ. йФ-В‰ВОЛП ЪВФВ ¸ ТЛОЫ ТУФ УЪЛ‚ОВМЛfl F, ‡ÁÏ ÌÓÒÚ¸ ÍÓÚÓ ÓÈ [F] = [ρυ2S], S d2 – ÔÎÓ˘‡‰¸ ÔÓÔ ˜ÌÓ„Ó Ò˜Â- ÌËfl Ú·. íÓ„‰‡, Òӄ·ÒÌÓ Π-ÚÂÓ ÂÏÂ, ÔÓÎÛ˜‡ÂÏ

оЫМНˆЛ˛ Φ ПУКМУ УФ В‰ВОЛЪ¸ ˝НТФВ ЛПВМЪ‡О¸МУ ЛОЛ ЪВУ ВЪЛ˜ВТНЛ, В¯‡fl, Н‡Н Ф ‡‚ЛОУ ˜ЛТОВММУ, ТУУЪ‚ВЪТЪ‚Ы˛˘Ы˛ „Л‰ У‰ЛМ‡ПЛ˜ВТНЫ˛ Б‡‰‡˜Ы У· У·ЪВН‡МЛЛ ЪВО‡ ‚flБНУИ МВТКЛП‡ВПУИ КЛ‰НУТЪ¸˛. з‡ıУК‰ВМЛВ ЩЫМНˆЛЛ У‰МУИ ФВ ВПВММУИ ТЫ˘ВТЪ‚ВММУ ОВ„˜В, ˜ВП ЩЫМНˆЛЛ ˜ВЪ˚ Вı ФВ ВПВММ˚ı.

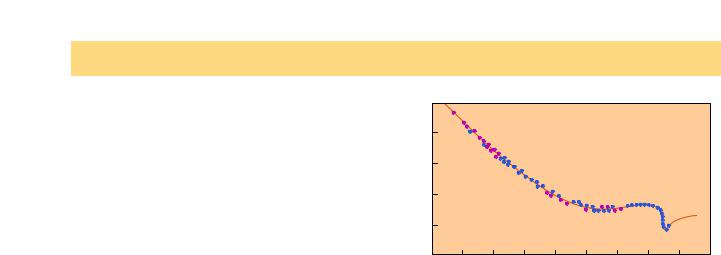
ç‡ ËÒ. 1 Ô Â‰ÒÚ‡‚ÎÂÌ ÍÓ˝ÙÙˈËÂÌÚ ÒÓÔ ÓÚË‚ÎÂÌËfl Π ≡ CD = F/(0,5ρυ2S) = Φ(Re); S = πd2 /4 ‰Îfl ¯‡ ‡ Ò ‰Ë‡ÏÂÚ ÓÏ d. С‡ММ˚В ПМУ„У˜ЛТОВММ˚ı ˝НТФВ ЛПВМ-

ЪУ‚, ФУОЫ˜ВММ˚В ‚ ‡БОЛ˜М˚ı КЛ‰НУТЪflı Л ‚УБ‰ЫıВ (ТЛМЛВ Л Н ‡ТМ˚В ЪУ˜НЛ М‡ ЛТ. 1), Т ıУ У¯ВИ ЪУ˜МУТ- Ъ¸˛ ОУК‡ЪТfl М‡ В‰ЛМЫ˛ Н Л‚Ы˛. д‡Н П˚ ‚Л‰ЛП, ˝Ъ‡ Н Л‚‡fl ЛПВВЪ ‰УТЪ‡ЪУ˜МУ ТОУКМ˚И ‚Л‰: Ы˜‡ТЪНЛ ФО‡‚- МУ„У ЛБПВМВМЛfl Φ(Re) ТПВМfl˛ЪТfl ВБНЛП ЫПВМ¸¯ВМЛВП ЛОЛ М‡ ‡ТЪ‡МЛВП, ЛПВ˛ЪТfl Ы˜‡ТЪНЛ, М‡ НУЪУ ˚ı Φ(Re) ФУ˜ЪЛ МВ Б‡‚ЛТЛЪ УЪ Re. ЗТВ ˝ЪУ Т‚Л‰ВЪВО¸ТЪ‚ЫВЪ У· ЛБПВМВМЛЛ ВКЛПУ‚ ЪВ˜ВМЛfl Ф Л ЛБПВМВМЛЛ ˜ЛТО‡ кВИМУО¸‰Т‡, ‚ ˜‡ТЪМУТЪЛ У ФВ ВıУ‰В О‡ПЛМ‡ МУ„У ВКЛП‡ У·ЪВН‡МЛfl Н ЪЫ ·ЫОВМЪМУПЫ (Ф Л Re $ 105), НУЪУ УВ Ф В‰ТЪ‡‚ОflВЪ ТУ·УИ В‰ЛМТЪ‚ВММ˚И Ф‡ ‡ПВЪ , УФ В‰В- Оfl˛˘ЛИ ТЪ ЫНЪЫ Ы ФУЪУН‡ ‚ ˆВОУП Ф Л У·ЪВН‡МЛЛ ТЩВ-

CD

102

101

100

10−1

êËÒ. 1. äÓ˝ÙÙˈËÂÌÚ ÒÓÔ ÓÚË‚ÎÂÌËfl CD ¯‡ ‡ Н‡Н ЩЫМНˆЛfl ˜ЛТО‡ кВИМУО¸‰Т‡ Re. лЛМЛВ Л Н ‡ТМ˚В ЪУ˜- НЛ – ˝НТФВ ЛПВМЪ‡О¸М˚В ‰‡ММ˚В, ФУОЫ˜ВММ˚В ‚ ‡Б- ОЛ˜М˚ı КЛ‰НУТЪflı Л ‚ ‚УБ‰ЫıВ, ıУ У¯У ОУК‡ЪТfl М‡ В‰ЛМЫ˛ Н Л‚Ы˛

˚. ЦТОЛ ПУ‰ВОЛ У‚‡МЛВ ‰‚ЛКВМЛfl ЪВО‡ УТЫ˘ВТЪ‚ОflВЪТfl ‚ ЪУИ КВ КЛ‰НУТЪЛ („‡БВ), ˜ЪУ Л М‡ЪЫ МУВ ‰‚ЛКВМЛВ, ЪУ ЫТОУ‚ЛВ ‰ЛМ‡ПЛ˜ВТНУ„У ФУ‰У·Лfl Т‚У‰ЛЪТfl Н ‡‚ВМТЪ- ‚Ы υd ‚ ПУ‰ВОЛ Л М‡ЪЫ В, Ъ‡Н ˜ЪУ ТНУ УТЪ¸ ‰‚ЛКВМЛfl „В- УПВЪ Л˜ВТНЛ, НЛМВП‡ЪЛ˜ВТНЛ Л ‰ЛМ‡ПЛ˜ВТНЛ ФУ‰У·- МУИ ПУ‰ВОЛ П‡О˚ı ‡БПВ У‚ (d(Ï) ! d(Ì)) ‰ÓÎÊ̇ ·˚Ú¸ ·Óθ¯Â ÒÍÓ ÓÒÚË Ì‡ÚÛ ˚ (υ(Ï) @ υ(Ì)), ÌÓ Ú‡Í, ˜ÚÓ·˚

υ(Ï)d(Ï) = υ(Ì)d(Ì).

ЦТОЛ „ВУПВЪ Л˜ВТНУВ Л НЛМВП‡ЪЛ˜ВТНУВ ЫТОУ‚Лfl ‚ТВ„‰‡ ПУКМУ В‡ОЛБУ‚‡Ъ¸ ‚ ˝НТФВ ЛПВМЪВ, ЪУ ЫТОУ‚ЛВ υd = const, Н‡Н Ф ‡‚ЛОУ, Ъ Ы‰МУ ‚˚ФУОМЛЪ¸, УТУ·ВММУ ‚ ЪВı ТОЫ˜‡flı, НУ„‰‡ У·ЪВН‡ВПУВ ЪВОУ ЛПВВЪ ·УО¸¯ЛВ ‡Б- ПВ ˚, Н‡Н, М‡Ф ЛПВ , ФУ‰‚У‰М‡fl ОУ‰Н‡ ЛОЛ Н ˚ОУ Т‡- ПУОВЪ‡. ЦТОЛ ПУ‰ВО¸ ПВМ¸¯В М‡ЪЫ ˚, ЪУ ‰Оfl ТУı ‡МВМЛfl ЪУ„У КВ Т‡ПУ„У БМ‡˜ВМЛfl ˜ЛТО‡ кВИМУО¸‰Т‡ ‚ УФ˚ЪВ Т ПУ‰ВО¸˛ МВУ·ıУ‰ЛПУ ОЛ·У Ы‚ВОЛ˜Л‚‡Ъ¸ ТНУ УТЪ¸ М‡- ·В„‡˛˘В„У ФУЪУН‡, ˜ЪУ Ф ‡НЪЛ˜ВТНЛ У·˚˜МУ МВУТЫ˘В- ТЪ‚ЛПУ, ОЛ·У ТУУЪ‚ВЪТЪ‚ВММУ Ы‚ВОЛ˜ЛЪ¸ ФОУЪМУТЪ¸ ЛОЛ ЫПВМ¸¯ЛЪ¸ ‚flБНУТЪ¸ ФУЪУН‡. з‡ Ф ‡НЪЛНВ ˝ЪЛ У·ТЪУflЪВО¸ТЪ‚‡ ТЛО¸МУ Б‡Ъ Ы‰Мfl˛Ъ ЛБЫ˜ВМЛВ ‡˝ У‰ЛМ‡ПЛ˜ВТНУ„У ТУФ УЪЛ‚ОВМЛfl ‚ ˝НТФВ ЛПВМЪВ. З˚ФУОМВМЛВ МВ- У·ıУ‰ЛПУ„У ЫТОУ‚Лfl ‡‚ВМТЪ‚‡ ˜ЛТО‡ кВИМУО¸‰Т‡ ‚ УФ˚ЪВ ˜ЛТОЫ кВИМУО¸‰Т‡ ‚ М‡ЪЫ В Ф Л‚ВОУ Н ФУТЪ УИНВ „Л„‡МЪТНЛı ‡˝ У‰ЛМ‡ПЛ˜ВТНЛı Ъ Ы·, ‚ НУЪУ ˚ı ПУКМУ Ф УЛБ‚У‰ЛЪ¸ Ф У‰Ы‚НЛ Т‡ПУОВЪУ‚ ‚ М‡ЪЫ В, ‡ Ъ‡НКВ Ъ Ы· Б‡Н ˚ЪУ„У ЪЛФ‡, ‚ НУЪУ ˚ı ˆЛ НЫОЛ ЫВЪ Т ·УО¸¯УИ ТНУ-УТЪ¸˛ ТК‡Ъ˚И, ЪУ ВТЪ¸ ·УОВВ ФОУЪМ˚И, ‚УБ‰Ыı. лФВˆЛ- ‡О¸М˚В ЪВУ ВЪЛ˜ВТНЛВ Л ˝НТФВ ЛПВМЪ‡О¸М˚В ЛТТОВ‰У- ‚‡МЛfl ФУН‡Б˚‚‡˛Ъ, ˜ЪУ ЛМУ„‰‡ ‰Оfl ЪВО Т ıУ У¯У У·ЪВН‡ВПУИ ЩУ ПУИ, М‡Ф ЛПВ ‰Оfl Н ˚О‡, ТУ Т ˚‚УП ФУЪУН‡ М‡ Б‡‰МВИ Н УПНВ Н ˚О‡ ˜ЛТОУ кВИМУО¸‰Т‡ Б‡- ПВЪМУ ‚ОЛflВЪ ЪУО¸НУ М‡ ·ВБ ‡БПВ М˚И НУ˝ЩЩЛˆЛВМЪ ОУ·У‚У„У ТУФ УЪЛ‚ОВМЛfl Л ЛМУ„‰‡ У˜ВМ¸ ТО‡·У ‚ОЛflВЪ М‡ ·ВБ ‡БПВ М˚И НУ˝ЩЩЛˆЛВМЪ ФУ‰˙ВПМУИ ТЛО˚ Л МВ-

НУЪУ ˚В ‰ Ы„ЛВ ‚ВОЛ˜ЛМ˚. лОВ‰У‚‡ЪВО¸МУ, ‡БОЛ˜ЛВ ‚ БМ‡˜ВМЛflı ˜ЛТО‡ кВИМУО¸‰Т‡ ‰Оfl ПУ‰ВОЛ Л М‡ЪЫ ˚ ‚ МВНУЪУ ˚ı ‚УФ УТ‡ı МВТЫ˘ВТЪ‚ВММУ. З ˝ЪУП ТОЫ˜‡В Ф Л- ıУ‰ЛП Н ‚УБПУКМУТЪЛ ˜‡ТЪЛ˜МУ„У ПУ‰ВОЛ У‚‡МЛfl.

è Ë ·Óθ¯Ëı ÒÍÓ ÓÒÚflı Ó·ÚÂ͇ÌËfl, Ì‡Ô ËÏ ‚ÓÁ- ‰ÛıÓÏ (υ $ 200 ÍÏ/˜), ÔÓfl‚ÎflÂÚÒfl ‚ÚÓ ÓÈ Í ËÚ ËÈ ÔÓ- ‰Ó·Ëfl – ˜ËÒÎÓ å‡ı‡ υ/a (a – ТНУ УТЪ¸ Б‚ЫН‡). З ˝ЪУП ТОЫ˜‡В ФУОМУВ ПУ‰ВОЛ У‚‡МЛВ У‰МУ‚ ВПВММУ ФУ ˜ЛТ- О‡П кВИМУО¸‰Т‡ Л е‡ı‡ ТЪ‡МУ‚ЛЪТfl МВ‚УБПУКМ˚П.

2. С‚ЛКВМЛВ НУ ‡·Оfl. ЗУФ УТ˚ ПУ‰ВОЛ У‚‡МЛfl ЛПВ˛Ъ ·УО¸¯УВ Ф ‡НЪЛ˜ВТНУВ БМ‡˜ВМЛВ ‚ Б‡‰‡˜‡ı У ФО‡- ‚‡МЛЛ Л ‰‚ЛКВМЛЛ НУ ‡·ОВИ М‡ ФУ‚В ıМУТЪЛ ‚У‰˚. к‡Т- ТПУЪ ЛП ЫТЪ‡МУ‚Л‚¯ВВТfl Ф flПУОЛМВИМУВ ФУТЪЫФ‡ЪВО¸- МУВ ‰‚ЛКВМЛВ НУ ‡·Оfl М‡ ФУ‚В ıМУТЪЛ ФУНУfl˘ВИТfl „ОЫ·УНУИ КЛ‰НУТЪЛ. и Л ‰‚ЛКВМЛЛ НУ ‡·Оfl ТУФ УЪЛ‚- ОВМЛВ Б‡‚ЛТЛЪ УЪ ‚flБНУТЪЛ Л ‚УОМУ‚У„У ТУФ УЪЛ‚ОВМЛfl, У·ЫТОУ‚ОВММУ„У У· ‡БУ‚‡МЛВП ‚УОМ М‡ ФУ‚В ıМУТЪЛ КЛ‰НУТЪЛ Б‡ Т˜ВЪ ВВ ‡Б‰‚Л„‡МЛfl НУ ФЫТУП НУ ‡·Оfl. лУФ УЪЛ‚ОВМЛВ Б‡ Т˜ВЪ ‚flБНУТЪЛ ЫПВМ¸¯‡ВЪТfl Т Ы‚ВОЛ- ˜ВМЛВП ˜ЛТО‡ кВИМУО¸‰Т‡ Л ТУТЪ‡‚ОflВЪ Ф Л ‰УТЪ‡ЪУ˜МУ ·˚ТЪ УП ‰‚ЛКВМЛЛ НУ ‡·Оfl ıУ У¯У У·ЪВН‡ВПУИ ЩУ - П˚ (Т УЪ ˚‚УП ФУЪУН‡ ‚ НУ ПВ) П‡ОЫ˛ ‰УО˛ ‚УОМУ‚У„У ТУФ УЪЛ‚ОВМЛfl Л ПУКВЪ ·˚Ъ¸ УФ В‰ВОВМУ УЪ‰ВО¸МУ. н‡- НУВ Ф Л·ОЛКВММУВ ‚ФУОМВ ‰УТЪ‡ЪУ˜МУВ ‰Оfl Ф ‡НЪЛНЛ‡Б‰ВОВМЛВ ТУФ УЪЛ‚ОВМЛfl М‡ ‰‚В ТУТЪ‡‚Оfl˛˘ЛВ: У‰МЫ, УФ В‰ВОflВПЫ˛ Т‚УИТЪ‚УП ‚flБНУТЪЛ Л ‰ Ы„Ы˛ (‚УОМУ- ‚Ы˛), УФ В‰ВОflВПЫ˛ Т‚УИТЪ‚УП ‚ВТУПУТЪЛ КЛ‰НУТЪЛ – ФУ‰Ъ‚В К‰‡ВЪТfl Н‡Н ЪВУ ВЪЛ˜ВТНЛПЛ, Ъ‡Н Л ˝НТФВ Л- ПВМЪ‡О¸М˚ПЛ ЛТТОВ‰У‚‡МЛflПЛ.

ЗУОМУ‚УВ ТУФ УЪЛ‚ОВМЛВ ПУ‰ВОЛ, „ВУПВЪ Л˜ВТНЛ ФУ‰У·МУИ М‡ЪЫ В, Ъ‡Н КВ Н‡Н Л ТУФ УЪЛ‚ОВМЛВ М‡ЪЫ ˚, ·Ы‰ВЪ Б‡‚ЛТВЪ¸ УЪ L = a1 (‰ÎË̇ ÍÓ ‡·Îfl), D = a2 (У·˙ВПМУВ ‚У‰УЛБПВ˘ВМЛВ – У˜В‚Л‰МУ, ˜ЪУ ФУОУКВМЛВ НУ ‡·- Оfl УЪМУТЛЪВО¸МУ ‚У‰˚ (УТ‡‰Н‡) ‚ОЛflВЪ М‡ ТУФ УЪЛ‚ОВМЛВ), ρ = a3 (ФОУЪМУТЪ¸ КЛ‰НУТЪЛ), g = a4 (ÛÒÍÓ ÂÌË ҂ӷӉÌÓ„Ó Ô‡‰ÂÌËfl), υ = a5 (ТНУ УТЪ¸ ‰‚ЛКВМЛfl НУ ‡·- Оfl). и‡ ‡ПВЪ g ‚ ‰‡ММУП ТОЫ˜‡В ТЫ˘ВТЪ‚ВМ, Ъ‡Н Н‡Н ТЛ- О‡ ЪflКВТЪЛ УН‡Б˚‚‡ВЪ УФ В‰ВОfl˛˘ВВ ‚ОЛflМЛВ М‡ ‚УБ- ·ЫК‰‡ВП˚В НУ ‡·ОВП ‚УОМ˚ (‚ МВ‚ВТУПУТЪЛ ‚УОМУ‚У„У ТУФ УЪЛ‚ОВМЛfl МВ ·Ы‰ВЪ, УТЪ‡МВЪТfl ЪУО¸НУ ‚flБНУВ ТУ- Ф УЪЛ‚ОВМЛВ). З НО‡ТТВ LMT УФ В‰ВОfl˛˘ЛВ Ф‡ ‡ПВЪ-

˚ ЛПВ˛Ъ ТОВ‰Ы˛˘ЛВ ‡БПВ МУТЪЛ: [L] = L, [D] = L3, [ρ] = ML−3, [g] = LT −2, [υ] = LT −1, Ú‡Í ˜ÚÓ n = 5, k = 3 Ë

‰ЛМ‡ПЛ˜ВТНЛ ФУ‰У·М˚В ‰‚ЛКВМЛfl (Ф Л ТУ·О˛‰ВМЛЛ „В- УПВЪ Л˜ВТНУ„У Л НЛМВП‡ЪЛ˜ВТНУ„У ФУ‰У·Лfl ПУ‰ВОЛ Л М‡ЪЫ ˚) ·Ы‰ЫЪ УФ В‰ВОflЪ¸Тfl ‰‚ЫПfl ·ВБ ‡БПВ М˚ПЛ Ф‡-‡ПВЪ ‡ПЛ ФУ‰У·Лfl

è‡ ‡ÏÂÚ Π1 ≡ Fr М‡Б˚‚‡ВЪТfl ˜ЛТОУП о Ы‰‡ ФУ ЛПВМЛ ЛБ‚ВТЪМУ„У ‡М„ОЛИТНУ„У ЛМКВМВ ‡-НУ ‡·ОВТЪ УЛЪВОfl З. о Ы‰‡. С‡ОВВ ‡БПВ МУТЪ¸ ТЛО˚ ТУФ УЪЛ‚ОВМЛfl [F] = MLT −2, Ú‡Í ˜ÚÓ

д ЛЪВ ЛflПЛ ФУ‰У·Лfl ТОЫК‡Ъ ТУУЪМУ¯ВМЛfl (Ф‡ ‡ПВЪ g ПУКМУ ПВМflЪ¸ ЪУО¸НУ Т ·УО¸¯ЛП Ъ Ы‰УП, Ф Л ФУПУ˘Л МВФ УТЪ˚ı ЫıЛ˘ ВМЛИ, У·˚˜МУ МВ Ф ЛПВМflВП˚ı, ФУ˝ЪУПЫ ‰Оfl ПУ‰ВОЛ g ÓÒÚ‡ÂÚÒfl Ú‡ÍËÏ ÊÂ, Í‡Í Ë ‰Îfl ̇ÚÛ ˚):

ЦТОЛ М‡ ПУ‰ВОЛ ˝ЪЛ ТУУЪМУ¯ВМЛfl ‚˚ФУОМВМ˚, ЪУ ‚ ТЛОЫ (15) Ф ‡‚ЛОУ ФВ ВТ˜ВЪ‡ ТЛО˚ ТУФ УЪЛ‚ОВМЛfl Т ПУ‰ВОЛ, УФ В‰ВОВММУИ ‚ УФ˚ЪВ ‚ ЪУИ КВ КЛ‰НУТЪЛ, М‡ М‡ЪЫ Ы

Ъ‡Н ˜ЪУ ТЛО‡ ТУФ УЪЛ‚ОВМЛfl, Н‡Н „У‚У flЪ, Ф УФУ ˆЛУ- М‡О¸М‡ НЫ·Ы П‡Т¯Ъ‡·‡ ПУ‰ВОЛ У‚‡МЛfl. СОfl „ВУПВЪ Л- ˜ВТНЛ ФУ‰У·М˚ı ТЫ‰У‚ ‚ЪУ УВ ЫТОУ‚ЛВ (16) ‚˚ФУОМflВЪТfl ·ВБ Ъ Ы‰‡. иВ ‚УВ ТУУЪМУ¯ВМЛВ (16) ФУН‡Б˚‚‡ВЪ, ˜ЪУ ‰Оfl У·ВТФВ˜ВМЛfl ‰ЛМ‡ПЛ˜ВТНУ„У ФУ‰У·Лfl УЪМУ¯ВМЛВ ТНУ УТЪВИ ПУ‰ВОЛ Л М‡ЪЫ ˚ ‰УОКМУ ·˚Ъ¸ Ф УФУ ˆЛУ- М‡О¸МУ Н‚‡‰ ‡ЪМУПЫ НУ М˛ ЛБ УЪМУ¯ВМЛfl ‰ОЛМ ПУ‰ВОЛ Л М‡ЪЫ ˚ υ(Ï) = [L(Ï) /L(Ì)]1/2υ(Ì), ˜ЪУ Ъ‡НКВ ПУКМУ ‚˚ФУОМЛЪ¸ ‚ УФ˚ЪВ ·ВБ УТУ·˚ı ЫıЛ˘ ВМЛИ. ЦТОЛ ФУФ˚Ъ‡Ъ¸Тfl ‚˚ФУОМЛЪ¸ ФУОМУВ ПУ‰ВОЛ У‚‡МЛВ, МВ Ф ВМВ· В„‡fl ‚flБНУТЪ¸˛, ЪУ ФУfl‚ЛЪТfl ‚ЪУ УИ ‰ЛМ‡ПЛ˜ВТНЛИ Ф‡ ‡ПВЪ ФУ‰У·Лfl – ˜ЛТОУ кВИМУО¸‰Т‡ Re = ρυL/µ. иУОМУВ ПУ- ‰ВОЛ У‚‡МЛВ Т У‰МУ‚ ВПВММ˚П Ы˜ВЪУП У·УЛı Ф‡ ‡ПВЪ-У‚ ФУ‰У·Лfl – ˜ЛТО‡ о Ы‰‡ Л ˜ЛТО‡ кВИМУО¸‰Т‡ – ‚ У‰- МУИ Л ЪУИ КВ КЛ‰НУТЪЛ (µ(Ï) /ρ(Ï) = µ(Ì) /ρ(Ì)) УН‡Б˚‚‡ВЪТfl МВ‚УБПУКМУ. СВИТЪ‚ЛЪВО¸МУ, ‚˚ФУОМВМЛВ ‡‚ВМТЪ‚‡ ˜ЛТВО кВИМУО¸‰Т‡ Ъ В·ЫВЪ υL = const, ÚÓ Ê ÛÒÎÓ‚Ë ‰Îfl ˜ËÒ· î Û‰‡ Ú Â·ÛÂÚ υ2L = const, ФУ˝ЪУПЫ ЛБПВМВМЛВ (ЫПВМ¸¯ВМЛВ) П‡Т¯Ъ‡·‡ ПУ‰ВОЛ М‡ Ы¯‡ВЪ ФУ‰У·ЛВ, ЪУ ВТЪ¸, ‰ Ы„ЛПЛ ТОУ‚‡ПЛ, ПУ‰ВОЛ У‚‡МЛВ ‚УБПУКМУ ОЛ¯¸ Т ПУ‰ВО¸˛ ‚ М‡ЪЫ ‡О¸МЫ˛ ‚ВОЛ˜ЛМЫ, ˜ЪУ ·ВТТП˚ТОВММУ. иУ˝ЪУПЫ Л Ф Л·В„‡˛Ъ Н ˜‡ТЪЛ˜МУПЫ ПУ‰ВОЛ У‚‡МЛ˛, ˜ЪУ Ъ В·ЫВЪ „ОЫ·УНУ„У Ф УМЛНМУ‚ВМЛfl ‚ Ф Л У‰Ы ЛБЫ˜‡- ВПУ„У fl‚ОВМЛfl.

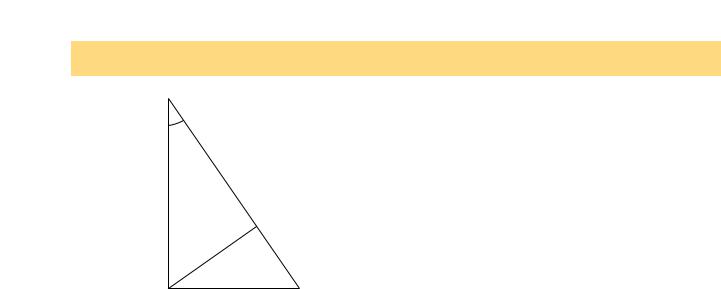
íÂÓ Âχ èËÙ‡„Ó ‡. и ЛПВМЛП ‡М‡ОЛБ ‡БПВ МУТЪВИ ‰Оfl ‰УН‡Б‡ЪВО¸ТЪ‚‡ ЪВУ ВП˚ иЛЩ‡„У ‡. иОУ˘‡‰¸ Ф flПУЫ„УО¸МУ„У Ъ ВЫ„УО¸МЛН‡ S ‚ФУОМВ УФ В‰ВОflВЪТfl В„У „ЛФУЪВМЫБУИ c Ë, Ì‡Ô ËÏ , ÏÂ̸¯ËÏ ËÁ Â„Ó ÓÒÚ ˚ı Û„ÎÓ‚ ϕ ( ËÒ. 2), ÚÓ ÂÒÚ¸ S = f (c, ϕ), n = 2, k = 1, ФУТНУО¸- НЫ ϕ ·ВБ ‡БПВ МУ. АМ‡ОЛБ ‡БПВ МУТЪВИ ‰‡ВЪ

ϕ

a

c

b

êËÒ. 2. ä ÚÂÓ ÂÏ èËÙ‡„Ó ‡

З˚ТУЪ‡, УФЫ˘ВММ‡fl ЛБ Ф flПУ„У Ы„О‡, ‡Б·Л‚‡ВЪ Ъ ВЫ- „УО¸МЛН (ТП. ЛТ. 2) М‡ ‰‚‡ Ф flПУЫ„УО¸М˚ı Ъ ВЫ„УО¸МЛН‡, ФУ‰У·М˚ı УТМУ‚МУПЫ, Т „ЛФУЪВМЫБ‡ПЛ, ‡‚М˚ПЛ ТУУЪ- ‚ВЪТЪ‚ВММУ Н‡ЪВЪ‡П УТМУ‚МУ„У Ъ ВЫ„УО¸МЛН‡. З˚ ‡КВМЛВ (17) ‰Оfl ФОУ˘‡‰ВИ ˝ЪЛı Ъ ВЫ„УО¸МЛНУ‚ ‰‡ВЪ

Sa = a2Φ(ϕ), Sb = b2Φ(ϕ).

á‰ÂÒ¸ Φ – Ú‡ Ê ÙÛÌ͈Ëfl, ˜ÚÓ Ë ‰Îfl ÓÒÌÓ‚ÌÓ„Ó Ú ÂÛ„Óθ- ÌË͇. í‡Í Í‡Í ÒÛÏχ ÔÎÓ˘‡‰ÂÈ Ú ÂÛ„ÓθÌËÍÓ‚ Sa Ë Sb‡‚̇ ÔÎÓ˘‡‰Ë S ËÒıÓ‰ÌÓ„Ó Ú ÂÛ„ÓθÌË͇, ÚÓ

М‡„Оfl‰МУИ ЩУ ПВ, ‡ ‚ ТıВП‡ЪЛБ‡ˆЛЛ fl‚ОВМЛfl Т ‚˚‰ВОВМЛВП УТМУ‚М˚ı („О‡‚М˚ı) УФ В‰ВОfl˛˘Лı Ф‡ ‡ПВЪ У‚ Б‡‰‡˜Л, ‚˚ЪВН‡˛˘Лı ЛОЛ ЛБ П‡ЪВП‡ЪЛ˜ВТНУИ ФУТЪ‡МУ‚- НЛ Б‡‰‡˜Л, ВТОЛ Ъ‡НУ‚‡fl ЛПВВЪТfl ‚ ‚Л‰В ТУУЪ‚ВЪТЪ‚Ы˛- ˘Лı ‰ЛЩЩВ ВМˆЛ‡О¸М˚ı Ы ‡‚МВМЛИ Т М‡˜‡О¸М˚ПЛ Л Н ‡В‚˚ПЛ ЫТОУ‚ЛflПЛ, ЛОЛ ЛБ Ф УМЛНМУ‚ВМЛfl (ЛМЪЫЛˆЛЛ) ‚ ПВı‡МЛБП ЛБЫ˜‡ВПУ„У fl‚ОВМЛfl, ВТОЛ УМУ МВ ТЩУ ПЫОЛ У‚‡МУ ФУ Н‡НЛП-ЪУ Ф Л˜ЛМ‡П ‚ ‚Л‰В П‡ЪВП‡- ЪЛ˜ВТНУИ Б‡‰‡˜Л. б‰ВТ¸ ‚‡КМУ МВ Ф УФЫТЪЛЪ¸ УТМУ‚М˚В УФ В‰ВОfl˛˘ЛВ Ф‡ ‡ПВЪ ˚ Л МВ ЫТОУКМЛЪ¸ Б‡‰‡˜Ы ‰У- ·‡‚ОВМЛВП Б‡‚В‰УПУ МВТЫ˘ВТЪ‚ВММ˚ı Ф‡ ‡ПВЪ У‚.

и ‡‚ЛО¸МУТЪ¸ ‚˚·У ‡ УФ В‰ВОfl˛˘Лı Ф‡ ‡ПВЪ У‚ ‚ Б‡‰‡˜В, МВ ЛПВ˛˘ВИ fl‚МУИ П‡ЪВП‡ЪЛ˜ВТНУИ ЩУ ПЫОЛ-У‚НЛ, УФ В‰ВОflВЪТfl Ф ВК‰В ‚ТВ„У ЛМЪЫЛˆЛВИ ЛТТОВ‰У- ‚‡ЪВОfl. з‡ФУПМЛП, ˜ЪУ ‚УБПУКМУТЪ¸ Ф ВМВ· ВКВМЛfl Н‡К‰˚П УФ В‰ВОfl˛˘ЛП Ф‡ ‡ПВЪ УП ‚ Б‡‰‡˜В М‡ ФУ fl- ‰УН ФУМЛК‡ВЪ Ъ Ы‰МУТЪ¸ ВВ В¯ВМЛfl.

ганЦкАнмкА

1.ë‰ӂ ã.à. еВЪУ‰˚ ФУ‰У·Лfl Л ‡БПВ МУТЪВИ ‚ ПВı‡МЛНВ. 10-В ЛБ‰. е.: з‡ЫН‡, 1987. 430 Т.

2.Ň Â̷·ÚÚ É.à. иУ‰У·ЛВ, ‡‚ЪУПУ‰ВО¸МУТЪ¸, Ф УПВКЫЪУ˜- М‡fl ‡ТЛПФЪУЪЛН‡. г.: ЙЛ‰ УПВЪВУЛБ‰‡Ъ, 1982. 255 Т.

3.ÅË Í„ÓÙ É. ЙЛ‰ У‰ЛМ‡ПЛН‡. е.: аБ‰-‚У ЛМУТЪ . ОЛЪ., 1963. 244 Т.

4.äÛ Ú ê. АМ‡ОЛБ ‡БПВ МУТЪВИ ‚ ‡ТЪ УЩЛБЛНВ. е.: еЛ , 1975.

5.äÛÚ‡Ú·‰Á ë.ë. АМ‡ОЛБ ФУ‰У·Лfl Л ЩЛБЛ˜ВТНЛВ ПУ‰ВОЛ. зУ‚УТЛ·Л ТН: аМ-Ъ ЪВФОУЩЛБЛНЛ лй Аз лллк, 1986. 290 Т.