1.19. Элементы Общей Теории Систем (Урманцева)

Общая Теория Систем начала разрабатываться Ю.А. Урманцевым в 1968 г. ОТС(У). В отличие от предшествующих системных теорий, ОТС (У) является аксиоматической теорией и она построена на аксиоматических предпосылках [44].

Какими должны быть предпосылки ОТС? Очевидно, теория, претендующая на предельную общность (всеобщность), должна исходить из всеобщих предпосылок, а таким требованиям отве­чают философские категории и законы. Поэтому, если мы хотим построить предельно общую теорию систем, она должна возводиться на фундаменте предпосылок, имеющих философский характер.

Для не полностью формализованной ОТС выбраны следующие пять аксиоматических условий:

Аксиомы ОТС(У):

1. Существование;

2. Множество объектов;

3. Единое;

4. Единство;

5. Достаточность.

Выбор аксиомы (1) обусловлен тем, что «су­ществование» является фундаментальной характеристикой сис­темы.

Су­ществование сводится к трем его формам:

• пространствен­ной;

• временной;

• динамической.

Из них особенно важна третья форма, т. е. движение.

Аксиома (2) – «множество объектов» понимается как множество самых различных объектов – материальных и идеальных. Фактически это «мир», каков он есть сам по себе, в его объективном существовании. «Объектом» мы называем любой предмет как объективной, так и субъективной реальности. Аксиома (2) приходится принимать во внимание потому, что невозможно построить систему, не имея нужных для этого объектов как своего рода строительных мате­риалов.

Аксиома (3) – «единое» представляет собой некоторое одинаковое для всех композиций («объектов-систем») данной системы («системы объектов данного рода») свойство (или признак), логически выступающее основанием классификации. В дальнейшем такие признаки мы будем называть признака­ми. Необходимость учета аксиомы (3) объясняется тем, что данную i-тую систему приходится строить из объектов лишь множества , выделенного по основанию и далее назы­ваемого множеством первичных элементов.

Аксиома (4) – «единство» понимается двояко:

• как отношение (в частном случае — взаимодействие) между «первичными» элементами, благодаря которому возникают объекты-системы, обладающие уже и новыми, целостными свой­ствами – аддитивными, неаддитивными, аддитивно-неадди-тивными;

• как отдельный объект – объект-система.

Аксиома (4) имеет фундаментальное значение для существования систем. Категория единства важна для ОТС, так как, благодаря ей конкретизируется проявление основного закона диалектики – закона единства и «борьбы» противоположностей

Аксиома (5) – «достаточность» понимается как, достаточность количества материала и необходимых условий для сооружения какого-либо объекта. Без достаточного количества «первичных» элементов, и достаточных оснований построение и существование какой бы то ни было системы невозможны. По сути дела, аксиома (5) совпадает с «принципом достаточного основания» Г. В. Лейбница, который писал в «Монадологии», что «ни одно явление не может оказаться истинным или дей­ствительным, ни одно утверждение справедливым без доста­точного основания, почему дело обстоит так, а не иначе...».

Предпосылки (1)-(5) и правила логики позволяют полу­чить все определения и предложения ОТС.

Таким образом, основу теории составляют некоторые положения или правила, которых всего пять. Все последующие утверждения выводятся формальным путем из этих пяти основных категорий. Рассмотрим основные положения этой теории.

К понятию объекта-системы мы пришли следующим образом. Пользуясь аксиомами (1)-(5), мы можем утверждать, что «существует множество объектов». Это означает, что мы образовали комбинацию (1) (2), которая сводится к утверждению о существовании так называемого универсального множества , принятого в теории множеств. Онтологически же это сужде­ние совпадает с суждением о существовании мира.

Далее принятые условия (предпосылки) позволяют утвер­ждать, что «существует множество объектов единых», что рав­носильно образованию комбинации (1, 2, 3). Этому размеще­нию отвечают находимые как в объективной, так и в субъектив­ной реальности специфические подмножества объектов , выделенные согласно признакам из существующего бесконечного множества объектов мира, т. е. из . Таким образом, любое равно или содержится в : . Такие подмножества – «множества первичных элементов» – могут быть конечными или бесконечными, размытыми или нераз­мытыми, одинаковой или разной мощности; они могут быть одно или разноэлементными, т. е. иметь простой или сложный состав.

Примеры множеств «первичных» элементов:

1) совокуп­ность атомообразующих элементарных частиц – протонов, нейтронов, электронов, которым соответствует множество призна­ков (индекс «a» – от слова «атом»);

2) совокупность «точек», «прямых», «плоскостей», позволяющих построить концептуальное пространство и выделенных согласно признакам (« » – от слова «пространство»);

3) совокупность отраже­ний в плоскостях – , позволяющих получить все классические симметрические преобразования, выделенные согласно признакам («с» – от слова «симметрия»).

Теперь в соответствии с предпосылками образуем комбина­цию – «существует единство множества объектов единых», или, что то же, «существует единство «пер­вичных» элементов». Эта комбинация означает, что выделенные по признакам объекты каждого существующего специ­фического множества объектов находятся в известных i-ых отношениях единства . Так, электроны, протоны, ней­троны могут вступить и вступают в атомообразующие отноше­ния – особого рода взаимодействия – ; «точки», «пря­мые», «плоскости» могут находиться, а в известных условиях и находятся в отношениях : «лежит на ...», «между», «конгруэнтны», «параллельны» .. .; плоскости отражения могут, согласно отношениям , пересекаться под всевозможными углами.

В силу двоякого смысла понятия «единство» комбинация означает и «существование нового объекта» как единства существующего множества единых объектов. В са­мом деле, единство протонов, нейтронов, электронов – это атом; единство «точек», «прямых», «плоскостей» суть концептуальное пространство; единство плоскостей отражения – симметриче­ское преобразование.

Наконец, необходимо учесть, что отношения единства , где бы они ни возникали (в природе или в уме человека), должны подчиняться требованиям определенных законов:

• атомообразую­щие взаимодействия – законам атомной физики;

• пространствообразующие – аксиомам связи, порядка, конгруэнтно­сти, непрерывности, параллельности и следующим из них теоре­мам;

• создающие симметрию – аксиомам теории групп

В силу сказанного правомерно следующее:

1) все объекты, возникаю­щие благодаря отношениям единства в соответствии с услови­ями из ряда объектов , назвать композициями или k;

2) участвующие в образовании композиций объекты из – «первичными» элементами»;

3) – i-ми множес­твами «первичных» элементов;

4) законы единения (условия, ограничивающие отношения единства) – законами композиции, или .

Теперь можно дать следующее определение объекта-системы.

Фундаментом общей теории систем Урманцева является представление о любом объекте окружающей материальной и идеальной действительности как об объекте-системе. Причем это понятие выводится из аксиом, которые являются базисом ОТС(У).

Определение 1.64. Объект-система - это композиция, или единство, построенное по отношениям (в частном случае - взаимодействиям) r множества отношений ( )и ограничивающим эти отношения условиям z множества из первичных элементов m множества , выделенного по основаниям а множества оснований из универсума U. При этом множества , и как порознь, так и совместно, могут быть пустыми или содержать , бесконечное число одинаковых или разных элементов.

Несмотря на внешнюю громоздкость, данное определение достаточно эвристично и отличается логической строгостью и одновременно простотой.

1. Система декларируется как некое единство, а не любая совокупность переменных (как, например, в кибернетической трактовке Эшби), что вполне отвечает общепринятым интуитивным представлениям.

2. В системе предполагаются отношения (взаимосвязи) между ее первичными (неделимыми на данном уровне рассмотрения) элементами, которые, в свою очередь, выделяются не произвольно, а лишь по вполне определенным правилам.

3. Сами же отношения при этом не любые, а ограничиваются некоторыми условиями (законами композиции), что устраняет неопределенность на стадии их установления.

4. В определении допускается существование пустых систем (нуль в математике, пустота в физике и т.д.), которые не находили должного отражения в прежних вариантах ОТС, впрочем, как и требование наложения на отношения ограничивающих условий.

5. Приведенное определение является универсальным и описывает любой объект или явление окружающей действительности.

Пример 1.6. Игра в футбол. Здесь можно выделить следующее:

• первичными элементами здесь выступают игроки обеих команд, мяч, ворота, судьи;

• первичные элементы связаны принадлежностью к полю, отношениями соперничества между командами и партнерства внутри команды;

• эти отношения ограничены определенными правилами игры, отличающими футбол, например, от регби.

Пример 1.7. В экономической системе первичными элементами являются субъекты хозяйствования, связанные между собой товарными, денежными, информационными потоками (отношениями), которые ограничиваются законами (условиями) – спроса, стоимости и т.д.

Пример 1.8. В формуле первичные элементы и связываются между собой арифметическими действиями (отношением), причем, только в единственном сочетании (условие) - чтобы сумма элементов и равнялась элементу .

Анализ примеров показывает, что с точки зрения ОТС(У) даже столь разные объекты, как футбол, экономика и формула имеют сходные черты.

Сходными чертами являются:

• все они состоят из первичных элементов ;

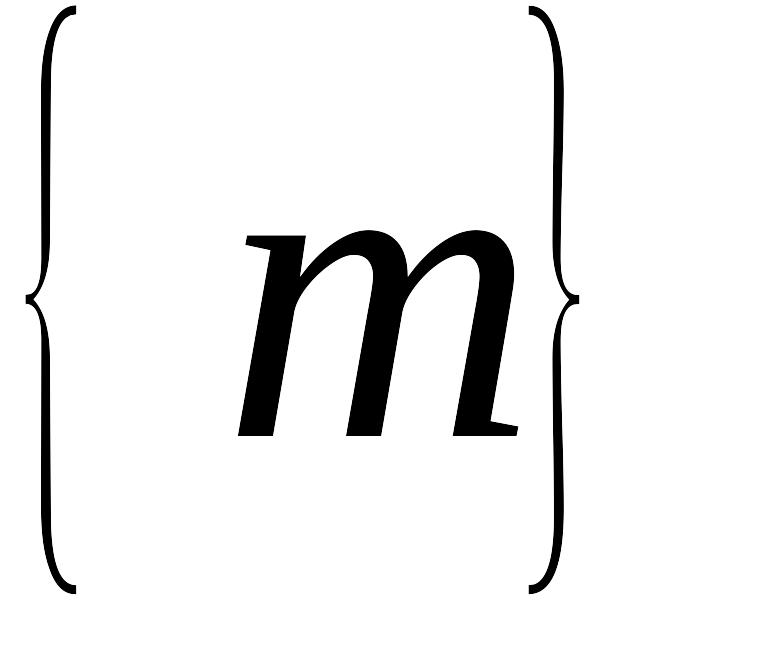• первичные элементы, связанны отношениями ;

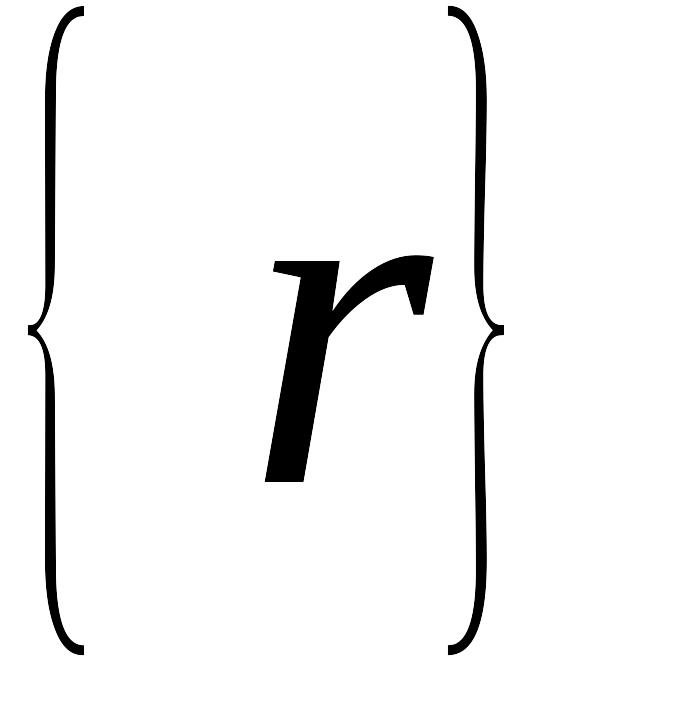• отношения ограничены условиями .

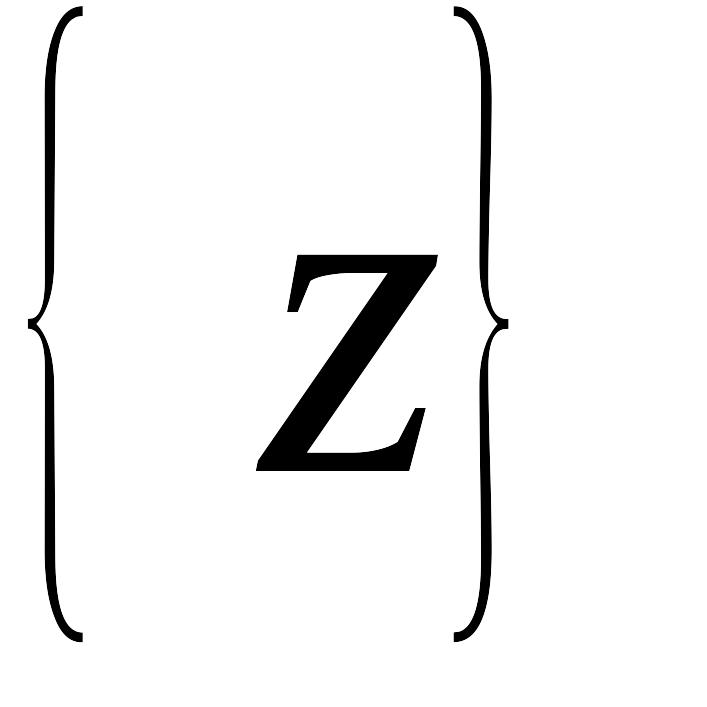Полученное обобщение является фундаментальным для последующего изложения.

Помимо определения объекта-системы в ОТС(У) вводится еще одно понятие, отсутствующее в прежних системных теориях: система объектов одного рода.

Определение 1.65. Система объектов одного рода – это закономерное множество объектов-систем одного и того же рода.

Определение 1.66. Выражение одного и того же рода означает, что каждый объект-система обладает общими, родовыми признаками (одним и тем же качеством), а именно: каждый из них построен из всех или части фиксированных первичных элементов в соответствии с частью или со всеми фиксированными отношениями, с частью или со всеми фиксированными законами композиции, реализованными в рассматриваемой системе объектов данного рода.

Введение этого понятия позволяет оперировать не только с абстрактными множествами, но и с родовыми понятиями - категориями естественными для биологических систем и человеческого общества.

Примером системы объектов одного рода может выступать множество всех игр с мячом, подмножествами которого являются конкретные игры – футбол, волейбол, баскетбол, регби и т.д.

Общими родовыми категориями для этого множества являются первичные элементы и отношения – во всех случаях мы имеем поле, команды, мяч, судей, связанных между собой сходными отношениями и различающимися лишь конкретными «законами композиции» или правилами игры.

Точно также по элементам и отношениям мы можем иметь множество экономик, отличающихся между собой законами функционирования или множество алгебраических преобразований, различных по последовательности операций.

Таким образом, представление конкретной системы в системе объектов одного рода открывает возможности для следующего уровня обобщения.

В сущности, основная сложность в использовании подхода «сверху» на практике заключается именно в обобщении привычных представлений и выходе на более высокий уровень описания исследуемых систем. Абстрагирование от конкретных «законов композиции» и переход к родовым категориям является в этом смысле отправной точкой для поиска и выявления общих свойств в системе объектов одного рода, которые по отношению к конкретным объектам являются надсистемными. Кроме этого, «поднявшись над системой», мы получаем возможность сравнивать законы композиции различных подсистем (например правила разных игр с мячом или закономерности функционирования разных экономических укладов), что способствует более ясному пониманию роли и места изучаемой системы среди аналогичных и открывает возможности для поиска нетривиальных аналогий и сходств