4 Теорема Остроградского-Гаусса и её применения для расчета поля

Тh. Поток вектора Е электрост. поля ч-з люб. замкн. поверхн. равен алгебраич. сумме зарядов, заключ. внутри данной поверхн. раздел. на электр. пост. . =

Пример 1. Равном. заряж. сфера R.

1) вне сферы ( >r), =

Алгоритм:

1: выбираем замкн. поверхность в виде сферы радиуса r

2: укажем направление вектора

3: проведем вектор внешней нормали = =| ↑↑ , =Е|= =E =E*S => =E*S

S=4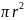 , = , E4 = => E= => E=k напряж. вне сферы

2) внутри сферы (r<R). =

=0 => Eв=0 напряж. внутри сферы

3) на поверхности (r=R). =0 – от центра к т. R. = k - извне

Пример 2. Объемно заряженный шар

1) внутри шара (r<R)

= , =E*S

S=4 r2, =ρ =ρ* r3

E4 r2= ρr - напряжение поля внутри шара

2) вне шара (r>R), E= k

3) = ρ* = ρ* , E=k = ρ

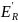= ρR - на поверхности

Пример 3. Равномерно заряж. плоскость.

= , в качестве замкнутой поверхн. выбираем цилиндр.

= + 2

= = | En2=0|=0

= = = E*Sосн

=2*E* Sосн, = * Sосн

2*E* Sосн= => E= однор. поле

5. Потенциал. Работа перемещения заряда в электрическом поле.

Потенциал (скаляр. величина) – энергетич. хар-ка электр. поля. Потенциал численно равен потенц. энергии единичного положит. заряда. , - потенц. энергия

Если некот. заряд q0 наход. в электр. поле, то на него действ. сила. Под действием силы заряд перемещается. В этом случае говорят, что совершается работа. Работа равна убыли потенц энергии, т.е. . Учит., что ; => A12=q0( - - работа перемещения заряда q0 из 1 т. поля в др. Работа перемещения заряда в электростат. поле не зависит от формы траектории, а опред-ся нач. и конеч. положениями зарядов. Если заряд перемещ-ся по замкн. траектории, то работа = 0.

Выраж-е для потенциала поля одного точечного заряда , где - коэф-т пропорц-ти, q – заряд, создающий поле, r – расст. от заряда до т., где вычисл. потенциал. Если поле создается системой зарядов, то потенциал результирующего поля равен алгебраич. сумме потенциалов полей, создаваемых кажд. зарядом системы в отдельн., т.е. Поверхность, все т. кот. имеют одинак. потенциал, назыв. эквипотенциальной: . Связь м-у напряженностью и потенциалом электростатич поля: ; .

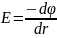6.Циркуляция вектора . Потенциальный характер электростатического поля.

Циркуляцией вектора вдоль замкн. контура L назыв. интеграл вида: . Работа перемещ. заряда в электрич. поле на элемент. перемещении: ,

- на элемент. перемещении, - на конкр. перемещении, =

.

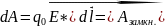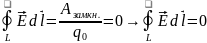Электрост. потенциал — скалярная энергетич. хар-ка электростат. поля, характериз. потенц. энергию поля, кот. обладает единичный заряд, помещ. в данную т. поля. Единицей измерения потенциала явл. единица измерения работы, деленная на единицу измерения заряда.

Потенц. характер, в частности, имеет электростат. поле точечного заряда.

Работу потенц. поля можно выразить ч-з изменение потенц. энергии. Формула справедлива для люб. электростат. поля. В случае однор. поля потенц. энергия выражается формулой

Потенц. энергия заряда в электростат. поле пропорциональна заряду. Это справедливо как для однородного поля, так и для неоднородного. Отношение потенц. энергии к заряду не зависит от помещенного в поле заряда.

Это позволяет ввести новую количественную характеристику поля - потенциал, не зависящую от заряда, помещенного в поле.

Для определения значения потенциальной энергии необх. выбрать нулевой уровень ее отсчета. При определении потенциала поля, созданного системой зарядов, предполаг., что потенциал в бесконечно удаленной т. поля равен 0. Потенциалом точки электростат. поля назыв. отношение потенц. энергии заряда, помещенного в данную т., к этому заряду.

Потенциал равен: . Напряженность поля E - векторная величина. Она предст. собой силовую хар-ку поля, кот. определяет силу, действующую на заряд q в данной точке поля. А потенциал - скаляр, это энергет. хар-ка поля; он определяет потенц. энергию заряда q в данной т.поля.

Теорема о циркуляции для электростатического поля – циркуляция вектора E по любому замкнутому контуру равна нулю, что означает потенциальность электростатического поля.

Потенциальным является любое центральное поле, в кот. сила зависит только от расстояния до силового центра и направлена по радиусу. Электростат. поле, создаваемое уединенным точечным зарядом, описывается законом Кулона. Это поле сферически-симметрично и представляет собой частный случай центрального поля. Отсюда следует потенциальный характер электростатического поля точечного заряда.