- •1.Электрические заряды и их свойства. Закон Кулона.
- •2. Электр. Поле в вакууме. Напряженность поля.
- •3.Линии напряженности электростатичекого поля. Поток вектора напряженности.
- •4 Теорема Остроградского-Гаусса и её применения для расчета поля
- •5. Потенциал. Работа перемещения заряда в электрическом поле.
- •6.Циркуляция вектора . Потенциальный характер электростатического поля.
- •7. Связь потенциала и напряженности поля. Эквипотенциальные поверхности.
- •8. Принцип суперпозиции. Вычисление поля диполя.
- •9. Диполь во внешнем однородном и неоднородном поле.
- •Поле не однородное (но симметрично вдоль оси ох)
- •10. Проводники во внешнем электростатическом поле. Электростатическая защита. Метод зеркальных изображений.
- •11. Электропроводимость уединенного проводника, конденсатора.
- •12.Вектор электрического смещения. Теорема Остроградского-Гаусса для поля в диэлектрике. Диэлектрики в эл. Поле.
- •13. Энергия системы неподвижных зарядов, заряженного проводника, заряженного конденсатора.
- •14. Энергия и плотность энергии электрического поля.
1.Электрические заряды и их свойства. Закон Кулона.
Сущ. 2 рода эл. зарядов: + и -.
q – электр. заряд (скаляр). [q]=1 Кулон=1 Кл.
Электр. заряды сущ. в виде элемент. заряж. частиц.
Элемент.
заряд:
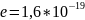 Кл.
Кл.
Св-ва электр. зарядов:
1)
электр. заряд дискретен (любой заряд
есть совок-ть элемент. зарядов).
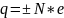
2) электр. заряд есть величина релятивистски-инвариантная (т.е.величина заряда не зависит от того, движется тело или покоится)
3) электр. заряды взаимодействуют. Одноим. отталкиваются, разноим. притягиваются.
4) закон сохр. электр. заряда: алгебр. сумма электр. зарядов люб. замкн. системы остается неизм., какие бы процессы не происходили внутри системы, т.е.: q1+q2+…+qn=const.
Точечный заряд – заряженное тело, размеры кот. весьма малы по сравнению с расстоянием до др. зарядов.
На практике имеем дело с телами, у которых заряд распределен непрер. по длине, поверхности, объему. Введем понятие плотности заряда:
1)
линейн. плотность
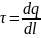 , [
, [ 1
Кл/м, для равном. распр. заряда:
1
Кл/м, для равном. распр. заряда:
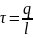
2)
поверхн. плотность
 , [
, [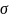 ]=1
Кл/
]=1
Кл/
3)
объёмная плотность
 , [
, [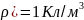 ,
,
dl,ds,dv – физически беск. малые: отрезок, площадь, объем.
Закон
Кулона:
 (только для точечн. электр. зарядов).
(только для точечн. электр. зарядов).
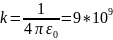 –
коэф-т
пропорц-ти,
–
коэф-т
пропорц-ти,
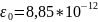 – электр. постоянная,
– электр. постоянная,
Закон
кулона для случая среды:
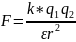 ,
где
,
где
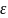 – относит. диэлектр. проницаемость
среды.
– относит. диэлектр. проницаемость
среды.
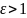 (кроме вакуума и воздуха
(кроме вакуума и воздуха
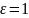 ).
).
2. Электр. Поле в вакууме. Напряженность поля.
Электр. поле материально. Основным св-вом электр. поля явл. то что на люб. др. заряд, помещенный в поле, действ. сила. В этом заключ. физич. механизм взаимод-я электр. зарядов. Рассм. поле точечного заряда:
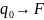
Если
в А поместить еще заряд (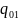 ):
):

Для
точки А:
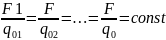
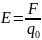 – напряженность
поля
– напряженность
поля
Напряженность (вект. величина) – силовая кол-венная хар-ка поля, численно равная силе, действующей на единичный положит. заряд.
Вектор Е совпад. с вектором F, действующей на q
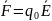
1)
 >0:
>0:
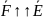 ,
2)
<0:
,
2)
<0:
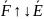
Формула
для расчета Е одного точечн. заряда q:
,
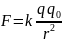 ,
,
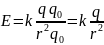
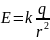 – напряженность
поля точечного заряда
– напряженность
поля точечного заряда
Принцип
суперпозиции:
Если электр. поле создается системой
зарядов, то напряженность результирующего
поля равна векторной сумме напряженности
полей, создаваемых кажд. зарядом системы
в частности:
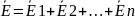 .
.
Если
заряд распределен по телу непрерывно
то:

3.Линии напряженности электростатичекого поля. Поток вектора напряженности.
Электростат. поле наглядно м-но изобразить с пом. силовых линий.
Силовой линией назыв. линию, касат. к кот. в люб. т. совпад. с вектором E. Линии вектора Е облад. рядом особенностей:
1) Нигде не пересек., т.к. вектор Е в кажд. т. простр-ва имеет лишь одно направление.
2) Имеют начало и конец. Начин. на положит. зарядах, заканчив. на отрицат.
3) С пом. линий Е м-но опред. не только направление, но и величину напряж-ти поля.
4) Линии Е проводятся с опред. густотой: число линий Е, пронизывающ. единицу поверхн., перпендик. линиям Е, должно быть = или пропорцион. величине Е.
Однородным назыв. поле, напряж-ть кот. остается пост. по величине и направлению.
Число линий Е, пронизыв. данную поверхн. S, назыв. потоком вектора напряженности. ФЕ-поток вектора Е
1) Поле однородное, поверхность плоская.
н айдем
проекцию вектора Е на направление
вектора нормали n
айдем
проекцию вектора Е на направление
вектора нормали n
Еn=Е*cosα, ФЕ=En*S => ФЕ=Е*S*cosα
2) Поле неоднородное, поверхность произвольная.

Разобьем поверхность S на БМ участки и выберем 1 из участков величиной ds. В пределах ds поле можно считать однор., а саму ds - плоской поверхн. Можем записать выраж-е для потока вектора ч/з поверхн. ds.
dФЕ=Ends=Eds*cosα,
а полный поток ФЕ= ds.
ds.
Введем
условн. вектор
 ,
,
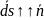 ,
тогда dФЕ=Ends,
тогда полный поток ФЕ=
,
тогда dФЕ=Ends,
тогда полный поток ФЕ=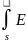 ds,
а поток ч-з замкн. поверхн. ФЕ=
ds,
а поток ч-з замкн. поверхн. ФЕ=